面向数控系统的容错实时调度算法研究

丁万夫 郭锐锋 秦承刚

1.中国科学院研究生院,北京,100039

2.中国科学院沈阳计算技术研究所,沈阳,110004

3.沈阳高精数控技术有限公司,沈阳,110171

0 引言

作为先进制造业的核心技术之一,数控技术的飞速发展,对实时计算提出了更高的要求。数控系统不仅需要保证位置控制、速度控制等实时周期性任务在规定的时限内完成,也要保证系统急停、参数调整等实时突发性任务的及时响应,而且在系统出现软硬件故障时,仍要保证系统安全正确地运行。因此,数控系统必须具有严格的时间确定性以及高度的可靠性。

目前,容错实时调度算法的计算模型可以分成两类:非精确计算模型[1-2]和软件容错模型[3-6]。在非精确计算模型中,每个任务由两部分组成:强制部分(mandatory part)和可选部分(optional part)。该模型中的调度算法首先保证强制部分按时完成,使得该任务的输出满足最低的需求,同时尽可能多地执行可选部分,以提高计算结果的精确性。非精确计算模型要求执行的任务具有单调性,即中间结果的精度不随执行时间的延长而下降,而数控系统则要求任务输出结果具有确定性的精度,因此该模型很难应用于数控系统。根据容错方式不同,软件容错模型又可分为主/替代版本模型[3-5]和回卷恢复模型[6],前者是一种基于软件冗余的容错技术。每个任务由两个版本组成:主版本(primary version)和替代版本(alternate version)。其中主版本计算时间较长,计算结果较为精确,但不保证程序完全正确地运行,而替代版本计算时间较短,只提供可接受的精度要求,但能够保证程序完全正确地运行,且两者只要求完成一个即可。回卷恢复模型是一种基于时间冗余的容错技术。在任务的执行过程中,每隔一定时间把任务的状态保存到可靠存储介质上(保存的状态称作检查点),而当系统发生故障时,回卷恢复模块读取保存的检查点文件,使得任务从该状态继续执行,把损失降低到检查点时刻到故障发生时刻这段时间内所做的计算。

在有关软件容错模型最新的研究成果中,文献[3]中提出了BCE算法,为软件容错模型提供了一种有效的实时调度策略。BCE算法包括Basic、CAT和 EIT三个子算法。在该算法中,主版本的预测精度是影响调度性能的关键。BCE利用CAT算法预测主版本的可执行性,但是当处理器利用率较高时BCE算法的调度性能很差。为了提高任务可执行性的预测精度,避免任务早期的失败对后续任务的影响,文献[4]提出了PKSA和CUBA算法。PKSA在BCE的基础上,通过K次试探性检测改进了对主版本可执行性的预测。CUBA算法则通过基于变动处理器利用率的试探性检测提高预测的准确性。文献[5]提出了DPA和EDPA算法。两种算法利用预测表对主版本的可执行性进行精确预测,尽可能地减少处理器时间浪费,为主版本提供更多的调度时间。由于上述算法只能调度单一类型的周期任务,因此均不适用于数控系统多种类型混合的任务调度。针对这一问题,文献[6]将人工智能领域的启发式搜索算法引入混合任务集优化调度研究,提出了最佳优先调度BF(Best First)算法来解决任务集的实时调度问题。在此基础上,提出了基于回卷恢复模型的容错调度策略,以提高数控系统运行的可靠性。但是该算法是基于时间冗余的容错机制,需要额外的运行开销,即在每个检查点,不仅需要对当前任务的执行状态(包括任务的数据变量和上下文环境)进行保存,而且还需要对任务执行结果的正确性进行测试,结果正确才可以保存此时的状态信息。可见,该算法容错时间开销较高,大大降低了系统资源利用率。

本文首先建立了数控系统混合任务调度的模型,提出了一种具有容错功能的实时调度算法FT—MT,在此基础上给出了该算法的伪代码描述以及实例研究,最后进行了调度算法的仿真实验。

1 系统、任务及容错模型

从任务组成来看,数控系统是一个典型的混合任务系统。其任务主要包括实时周期任务、实时突发任务和非实时任务。根据任务的关键度不同,又可将实时周期任务分为有容错需求的实时周期任务和无容错需求的实时周期任务。

定义1 有容错需求的实时周期任务集合Γfrp={τi},i=1,2,…,n,其中 n为该类任务的总数。 ∀τi∈ Γf rp由一个无限的作业序列 τi={τi1,τi2,…}构成,其中第 j个作业τij可用六元组表示为 :τij=(Ti,Ri,Pij,Aij,Ci,),其中 Ti为作业的周期,Ri为作业的到达时间,Pij和Aij分别为τij的主版本和替代版本,Ci和分别为Pij和Aij的执行时间,且Ci≥。

定义2 无容错需求的实时周期任务集合Γnfrp={τi},i=n+1,n+2,…,n+m,其中 m 为该类任务的总数。∀τi∈Γnfrp由一个无限的作业序列 τi={τi1,τi2,…}构成 ,其中第 j个作业τij只有一个运行版本,可用四元组表示为:τij=(Ti,Ri,Aij,),其中Ti为作业的周期,Ri为作业的到达时间,Aij为τij的运行版本,为Aij的执行时间。

由定义1和定义2可知,实时周期任务集合Γrp可表示为 Γfrp与 Γnfrp的并集 ,即 Γrp=Γfrp∪Γnfrp={τ1,τ2,...,τn+m}。在本文中 ,规定所有实时周期任务在周期开始时已准备就绪,而周期的结束时刻为任务的截止期。

定义3 实时突发任务集合Γap={Si},i=1,2,…,n。 ∀Ai∈ Γap可用三元组表示为:Si=(Ci,Ri,Di),其中Ci为执行时间,Ri为到达时间,Di为任务的截止期。

定义4 非实时任务集合 Γnr={Ni},i=1,2,…,n。 ∀Ni∈ Γnr可用二元组表示为:Ni=(Ci,Ri),其中Ci为任务的执行时间,Ri为任务的到达时间。

定义5 替代版本在其截止期内的最迟开始时间称为该替代版本的临界点。

本文研究的前提条件:

(1)本容错模型仅考虑单处理机系统的软件错误。由于主版本提供了更为精确的计算结果,因此调度算法将尽可能多地执行主版本,而当主版本不能在替代版本的开始时间之前完成时,则必须执行替代版本,以保证任务在其截止期之前能够获得可以接受的计算结果。

(2)在运行过程中,规定替代版本具有最高的优先权,实时突发任务的优先权高于实时周期任务的优先权,而非实时任务具有最低的优先权。

2 问题描述

2.1 Basic算法介绍

文献[3]提出了一种基于RM算法的软件容错模型,该模型的核心算法是Basic算法。运行前,Basic算法为替代版本预先分配执行区间,使得替代版本在其截止期内尽可能地推迟执行,从而为主版本的完成提供了最大的可执行时间。运行时,所有的主版本都在余下未被分配的区间内执行。对于是否执行替代版本,主要有两种可能:

(1)如果主版本在其替代版本的通知时间到来之前运行完毕,系统将撤销替代版本,然后调整相应受影响的其他替代版本的时间间隔,并计算新的通知时间。

(2)如果主版本在其替代版本的通知时间到来时没有完成,系统将撤销该主版本,其替代版本开始运行。

2.2 Basic算法存在的问题

在RM算法下,考虑一个包含两个实时周期任务的任务集合 Γfrp={τ1,τ2},参数 τij=(Ti,Ri,Pij,Aij,Ci,)分别是(5,0,P1j,A1j,2,1)和(6,0,P2j,A2j,2,2),因此 HP=LCM(5,6)=30。如图1所示,在区间[0,30],两个任务的通知时间分别是 v1j=4,9,14,19,24,29(j=1,2,…,6)和v2j=3,10,16,22,27(j=1,2,…,5)。这种为替代版本分配通知时间的方法称为反向速率单调(backwards—RM)算法。

下面介绍Basic算法存在的主要问题。图2所示为该任务集的运行情况。在时刻0,具有较高优先级的主版本P11就绪并开始执行,假设P11由于软件错误在时刻2失败,所以预留给A11的区间[4,5]不能被撤销。在时刻2,P21开始运行,在时刻3,A21的通知时间到了,由于替代版本的优先级高于所有主版本的优先级,因此,A21抢占P21执行。同理,在接下来的区间[4,5]和[5,6],系统分别运行 A11和A21。在时刻 6,P12和P22同时就绪,由于P12的周期较P22短,所以系统执行P12。假设P12在时刻8执行完毕,那么分配给A12的区间[9,10]就不再需要,系统撤销了A12。接着P22开始执行并且在时刻10执行完毕,所以A12也被系统撤销。在时刻10,P13开始运行,假设P13在时刻12发生错误,P23在时刻12被选择运行,并在时刻14运行完毕。由于P13出错,所以 A13不可以被撤销,在时刻14,A13开始执行。

观察图2可以发现,在时刻12,虽然P13执行失败,但仍有足够的时间使得P13重新执行一次,这反映了Basic算法的局限性。

3 混合任务集的容错调度算法FT—M T

3.1 FT—MT算法

针对数控系统的混合任务调度以及高可靠性的特点,本文提出一种基于软件容错模型的实时调度算法 FT—MT(fault tolerance for mixed tasks),该算法在系统运行前预先分配替代版本的执行区间,使得替代版本在其截止期内尽可能地推迟执行,从而为主版本的完成提供了最大的可执行时间。系统在运行过程中以替代版本的临界点作为主版本新的截止期,按照速率单调算法调度所有的主版本。如果主版本在其替代版本的临界点之前运行完毕,系统将撤销替代版本,否则系统将撤销该主版本,开始执行替代版本,以保证在任务截止期之前能够获得可接受的计算结果。通过主版本重新执行规则以及优先级提升规则来尽最大努力地提高主版本的完成率,以改善输出结果的计算精度。

3.1.1 主版本重新执行规则

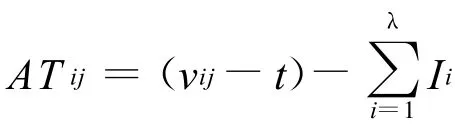
如图3所示,通知时间为vij的主版本Pij在时刻t开始执行,在时刻t′执行失败,假设在区间[t,vij]内,有λ个已经被分配出去的区间{Ii|i=1,2,…,λ}。

定义6 重新执行可获得时间OTR(obtainable time for re—execution)定义如下:

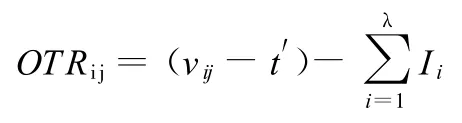
主版本重新执行规则:当且仅当主版本Pij的执行时间Ci小于或者等于OTRij,主版本Pij才可以重新执行,否则系统撤销Pij的执行。

如图4所示,在时刻 12,P13出错,由于OTR13=2,等于P13的执行时间,根据FT—M T算法的重新执行规则,系统在时刻12重新执行P13。P13在时刻14运行完毕,A13被系统撤销。在时刻14,由于只有P23就绪,系统将选择P23运行。在这个例子中,通过重新执行主版本P13,使得P13和P23都顺利完成,提高了主版本的完成率,改善了输出结果的计算精度。

3.1.2 主版本优先级提升规则

为了验证优先级提升规则的有效性,再来看一个例子 。给定任务集 Γfrp={τ1,τ2},参数 τij=(Ti,Ri,Pij,Aij,Ci,)分别是(3,0,P1j,A1j,1.5,1)和(5,0,P2j,A2j,1,1),因此 HP=LCM(3,5)=15。如图5所示,在时刻 0,P11与 P21都已就绪,由于P11的周期较短,根据RM调度规则,系统将选择 P11运行。P11在时刻 1.5运行完毕,所以系统撤销了A11。在时刻1.5,P21开始执行,假设P21在时刻1.5发生错误。由于在时刻2.5没有其他就绪的任务,并且 P21的OTR21为1.5,等于 P21的执行时间,根据Kernel算法重新执行规则,系统将重新执行P21。在时刻3,P12就绪,由于P12的优先级高于 P21,所以P12抢占 P21开始运行。因为时刻4是替代版本A21的通知时间,而替代版本的优先级高于所有主版本的优先级,所以A21抢占 P12开始运行。在时刻 5,A21运行完毕,又因为时刻5是A12的通知时间,所以系统撤销了P12,转而运行A12。

在上例中,由于P12抢占了 P21,这导致两个主版本都未能按时完成。为了解决这个问题,需要给FT—MT算法增加一条新的规则,即优先级提升规则,来保证重新执行的任务不会被高优先级任务抢占。但是注意,提升之后的优先级仍然不会高于替代版本的优先级。

主版本优先级提升规则:假设主版本Pij出错前和出错后的优先级分别是pi和api,且api≥pi,如果∃m,n使得 Pmn∈Γ,那么 Pmn可以抢占Pij(当且仅当Pmn的优先级pm大于api)。

如图6所示,在时刻3,虽然 P12已经就绪,根据FT—MT算法的优先级提升规则,P12无法抢占P21,因此,P21可以继续执行,并在时刻3.5运行完毕,同时系统撤销A21。在时刻3.5,P12开始运行,并在时刻 5运行完毕,A12也被系统撤销。可以看到,增加优先级提升规则后的FT—MT算法进一步提高了主版本的完成率。

3.2 算法FT—MT的描述

文献[3]提出的CAT算法和EIT算法能够进一步提高Basic算法的性能。算法FT—MT调用CAT算法预测主版本的可执行性,如果该主版本满足可执行的条件,则执行该主版本,否则,取消该主版本。当处理器处于空闲状态时,算法FT—MT调用EIT算法提前执行替代版本,为其他主版本留出更多的调度时间。如图6所示,在区间[7.5,9]内,由于既没有就绪待执行的主版本,也没有通知时间已到的替代版本,使得处理器处于空闲状态。显然,通过将FT—MT算法和EIT结合,当处理器处于空闲状态时,系统就可以提前执行替代版本,从而避免了处理器空闲的情况。图7给出了F T—MT算法的伪代码。

3.3 举例

本节以数控系统中的混合任务调度为例说明FT—MT算法的调度过程。为简化分析,假设混合任务集中包括四个任务,其中两个实时周期任务,一个实时突发任务和一个非实时任务。各任务的参数描述如表1所示。

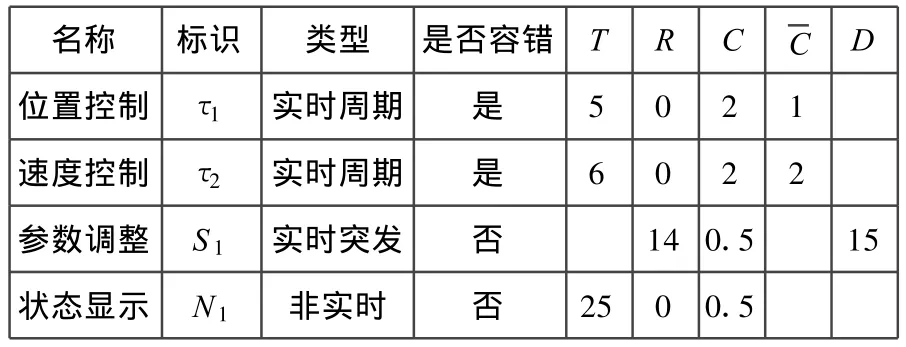
表1 任务参数

首先按照反向速率单调算法为替代版本分配执行区间。在区间[0,30],替代版本的临界点分别是v1j={4,9,14,19,24,29}(j=1,2,…,6)和v2j={3,10,16,22,27}(j=1,2,…,5)。

下面介绍FT—MT算法的调度过程。图8所示为该任务集的运行过程。在时刻0,具有较高优先级的主版本P11就绪并开始执行,假设P11由于软件错误在时刻2失败,所以预留给A11的区间[4,5]不能被撤销。在时刻2,P21开始运行,在时刻3,A21的临界点到了,由于替代版本的优先级高于所有主版本的优先级,因此,A21抢占P21执行。同理,在接下来的区间[4,5]和[5,6],系统分别运行A11和A21。在时刻6,P12和P22同时就绪,由于P12的周期较P22短,所以系统执行P12。假设P12在时刻8执行完毕,那么分配给A12的区间[9,10]就不再需要,系统撤销了A12。接着P22开始执行并且在时刻10执行完毕,所以A12也被系统撤销。在时刻10,P13开始运行,假设P13在时刻12发生错误,由于OTR13=C13=2,等于P13的执行时间,根据FT—MT算法的重新执行规则,系统在时刻12重新执行P13。P13在时刻14运行完毕,A13被系统撤销。在时刻14,P23和实时突发性任务S1同时就绪,由于S1的优先级较高,系统选择S1运行,在时刻14.5,S1执行完毕。由于OTR23=1.5＜C23=2,根据FT—MT算法的首次执行规则,系统撤销P23,开始执行N1并在时刻15执行完毕。P14在区间[15,16]和[18,19]执行,而 A23在区间[16,18]执行。

4 仿真实验

为了对比不同调度算法的容错能力,本文定义了两个衡量容错算法性能的指标:主版本成功率(success rate of primary,SRP)和任务成功率(success rate of tasks,SRT)。SRP是主版本的实际完成数量与主版本总数量的比值,该指标衡量容错调度算法输出结果的计算精度。SRT是任务的实际完成数量与任务总数量的比值,该指标衡量容错算法对于混合任务的调度性能。

具体实验环境如下:

硬件平台:Intel(R)Pentium(R)M,1.73GHz,512MB

软件平台:REDHAT7.0

实时内核:Linux—2.4.20+RTAI3.1

本次仿真实验共模拟了1000组任务集,每组任务集包括100个任务,任务集中各种任务的类型及所占比例如表2所示。对于任意给定的任务τi,其周期 Ti,截止期Di,执行时间Ci和替代版本的执行时间以及任务集的错误率f p都是随机产生的,但需要满足Di=Ti≥Ci≥2＞0且f p＞0。

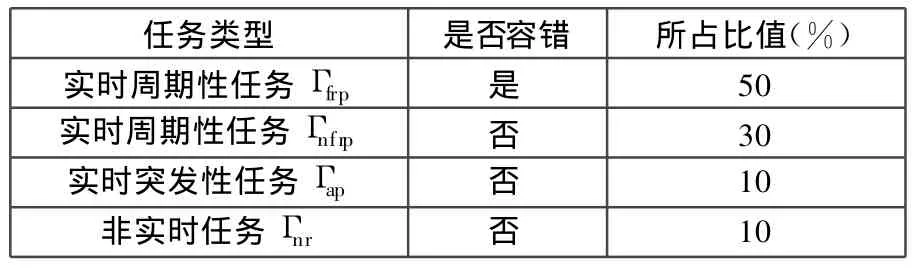
表2 任务类型及所占比例

4.1 仿真实验1

本实验测试了FT—MT算法在不同的处理机利用率U下SRP值的变化情况。该实验测试了f p=0.05、fp=0.1和 fp=0.15三种情况下FT—MT算法的SRP值,如图9所示,结果表明:

(1)当处理机利用率U低于55%时,FT—MT算法的SRP值始终保持在100%,即所有的主版本都能在其替代版本的临界点到来之前运行完毕。

(2)随着处理机利用率U的增加(高于55%),对于不同 f p值,FT—MT算法的SRP值逐渐减少,且任务集的错误率 fp越大,SRP值下降得越快。这是因为U值越大,表明任务主版本的资源需求越大,因此所能完成主版本的数量就越少,而 fp越大,即主版本出错的概率越大,导致所能完成主版本的数量越少。

4.2 仿真实验2

本实验比较了FT—MT和BF两种算法在处理混合任务集时的调度性能,实验中错误率 f p的变化范围是[0.05,0.25],处理机利用率U的变化范围是[0.01,0.9]。如图10所示,两种算法的任务成功率SRT值都表现出了一种由高到低的趋势。比较图10a和图10b可以发现,在容错能力方面FT—MT算法明显优于BF算法。这是因为BF算法的容错机制是基于时间冗余的,需要额外的运行开销,即不管主版本是否发生错误,系统都需要保存每个检查点的状态信息,导致当错误率和处理机利用率都较高时任务的成功率很低,而FT—MT算法在主版本不发生错误时,不需要额外的运行开销,只有当主版本无法完成时才执行替代版本以达到容错目的,因此使得主版本运行正确的概率大大增加。

5 结束语

作为实时系统的一种典型应用,数控系统有其自身的要求。除了具有严格的实时性以及高度的可靠性之外,数控系统还需要进行多种类型任务并存的混合任务调度。本文首先分析了不同容错模型的特点,提出了基于主/替代版本的软件容错实时调度算法(FT—MT),通过推迟替代版本在其截止期内的执行,提高了主版本的完成率,改善了系统输出结果的计算精度,同时增加了主版本的可执行规则,提高了主版本可执行性的预测精度,有效减少了浪费的处理机时间。FT—MT算法实现简单,运行开销小,资源利用率高,能为系统提供容错支持,完全满足数控系统对实时性及可靠性的要求。

[1]Zhang Y X,Fang G H,Wang Y.A Feedback—driven Online Scheduler for Processes with Imprecise Computing[J].Journal of Software,2004,15(4):616-623.

[2]陈宇,熊光泽.基于资源回收的容错最早时限优先调度[J].系统工程与电子技术,2003,25(10):1274-1277.

[3]Han C C,Shin K G,Wu J.A Fault—tolerant Scheduling Algorithm for Real—time Periodic Tasks with Possible Software Faults[J].IEEE Transactions on Computers,2003,52(3):362-372.

[4]李庆华,韩建军,AAEssa,等.硬实时系统中基于软件容错的动态调度算法[J].软件学报,2005,16(1):101-107.

[5]刘东,张春元,李瑞,等.软件容错模型中的容错实时调度算法[J].计算机研究与发展,2007,44(9):1495-1500.

[6]姚鑫骅,傅建中,陈子辰,等.面向数控系统的优化调度算法及容错策略研究[J].计算机集成制造系统,2007,13(4):768-776.