壳结构声场耦合分析的光滑有限元—有限元法

姚凌云 于德介 臧献国

湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082

0 引言

壳体结构广泛应用于汽车车身、飞机、潜艇等工程结构中,其结构—声场耦合产生的振动与噪声问题引起了越来越多的关注。壳体结构在激励作用下会产生振动,并与其周围的声场产生耦合,从而向声场辐射噪声。壳体的结构—声场耦合分析在工程实际中有着非常重要的作用,对壳体结构的噪声与振动控制研究有十分重要的意义。壳体的结构—声场耦合系统是结构和声场相互作用的复杂动力学系统,包括壳体结构域、声场域,以及两个域之间的耦合作用。快速、准确地预测其结构—声场耦合系统的声学响应是近年来结构噪声控制研究领域的热点之一。

目前,壳体的结构—声场耦合的分析方法有解析法和数值法,其中数值法主要包括有限元—有限元法[1-5](finite element method,FEM)、有限元(FEM)—边界元法[6-7](boundary element method,BEM)、有限元—无限元法[8](infinite element method,IEM)等。FEM/FEM和FEM/BEM是结构—声场耦合分析中最常用的计算方法,在一些大型的商业软件如Nastran、Sysnosie等中应用广泛。与FEM/FEM相比,FEM/BEM能减少模型的单元数量,但其矩阵为非稀疏阵,并不一定能够提高计算效率,对于内部问题,FEM/FEM计算效率往往更高一些。FEM/FEM和FEM/BEM主要用于结构—声场耦合低频计算且受模型网格尺寸特别是结构网格尺寸的影响较大。

光滑有限元法(smoothed finite element method,SFEM)是 Liu[9-10]针对有限元法过于“刚硬”的问题,将标准的有限元法与无网格中分区应力光滑技术相结合提出来的。SFEM不仅解决了四边形单元扭曲严重时计算误差大的问题,还能提高计算效率和计算精度。Cui等[11]将SFEM应用到解决板壳的线性和几何非线性问题中,结果表明SFEM具有很好的稳定性和精度。Dai等[12]将SFEM应用到二维动力学问题中分析结构自由振动和强迫振动问题。Nguyen等[13]将SFEM应用到Mindlin—Reissner板的力学分析中,用曲率光滑方法(curvature smoothing method,CSM)计算板的弯曲刚度矩阵,结合MITC4单元解决了剪切自锁问题,提高了计算精度。Nguyen等[14]在上述工作的基础上应用SFEM分析壳结构的静力学特性。

为了提高结构—声场耦合分析精度,降低结构—声场耦合分析中对结构网格的尺寸要求,本文将SFEM推广到壳结构动力学分析中,结合流体FEM分析壳结构—声场耦合问题,并推导了SFEM/FEM计算壳的结构—声场耦合公式。运用SFEM/FEM分析结构—声场耦合系统时,壳体结构域应用分区应力光滑技术对弯曲应力和膜应力进行光滑处理;剪应力由MITC单元应用独立插值函数获得[15];在流体域应用传统的FEM进行分析。由于SFEM/FEM继承了SFEM计算简单、精度高的特点,在分析壳结构—声场耦合时比FEM/FEM的精度和计算效率更高,对结构网格尺寸要求更低。以六面体结构—声场耦合模型和微车内声固耦合模型为数值算例,研究结果表明:与 FEM/FEM相比,SFEM/FEM的精度和效率更高,对网格尺寸的质量要求更低,能很好地应用于壳结构—声场耦合分析中,具有良好的工程应用前景。

1 基于SFEM/FEM的结构—声场耦合分析

1.1 壳结构的SFEM模型原理

根据第一剪切变形理论,如图1所示,壳结构的位移分量u、v和w可分别表示为

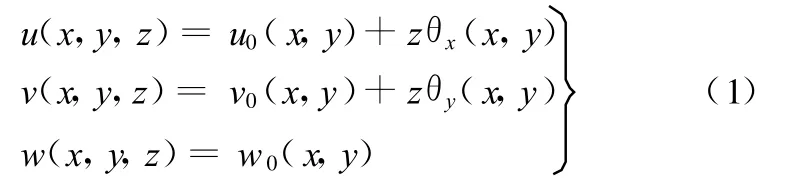
式中,u0、v0、w0分别为壳中面 x、y、z三个方向的位移;θy、θx分别为xz和yz平面内的转角。

定义ε为应变矢量:

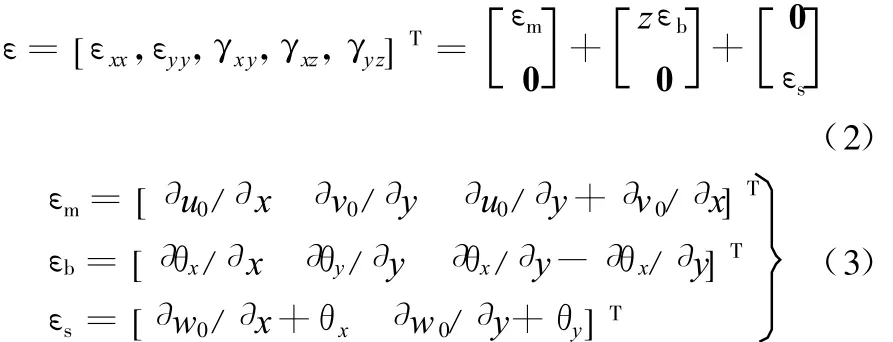
式中,εm为膜应力矢量;εb为弯曲应力矢量;εs为剪切应力矢量。

壳结构的弯曲刚度本构矩阵Db、横向剪切刚度本构矩阵Ds和膜刚度本构矩阵Dm可分别表示为

式中,E为弹性模量;ν为泊松比;kτ为剪切修正系数;t为壳单元厚度。

根据标准的FEM,将壳结构域 Ω离散为Ne个四边形单元,包含Nd个节点。设壳单元节点位移矢量 u=(u,v,w,θx,θy)T,则单元中面上的位移近似为

式中,dI为I节点的位移;NI为形函数。

将SFEM四边形单元划分为SC个光滑域,以满足Ω1∪ Ω2∪ …ΩSC=Ω和 Ω1∩ Ω2∩ …ΩSC=∅,其中 ∅表示空集,研究表明光滑域的最优个数为3[9]。节点处的形函数值为(N1,N2,N3,N4);积分点处的形函数值从光滑域边界上线性插值得到[12]。图 2所示为单元光滑域(smoothing cells,SC)划分及其形函数值(SC=1,4)。

应用光滑处理技术对壳单元的第C个光滑域进行光滑处理,光滑膜应力和光滑弯曲应力

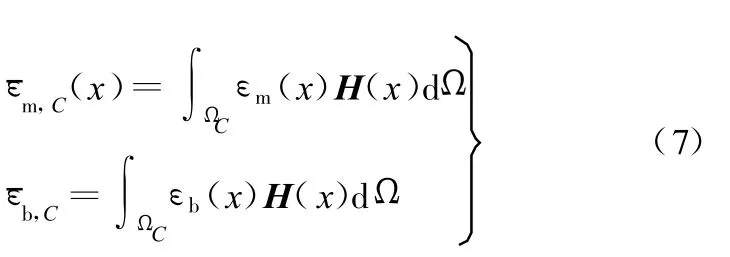
式中,H(x)为光滑函数。

在本文中采用常值光滑函数:

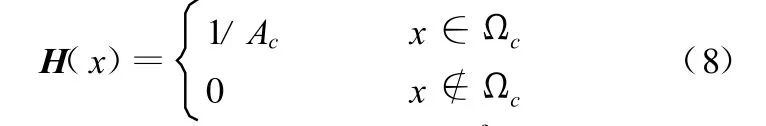
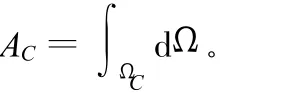
将式(6)、式(8)代入式(7),并利用散度定理,有

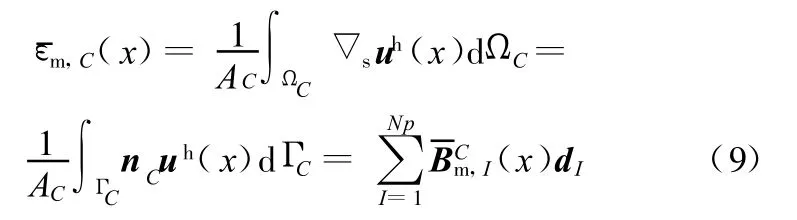
式中,ΓC为光滑域的边界;nC为光滑域边界的外法向单位矢量。

其中,微分算子为

光滑膜应力矩阵为

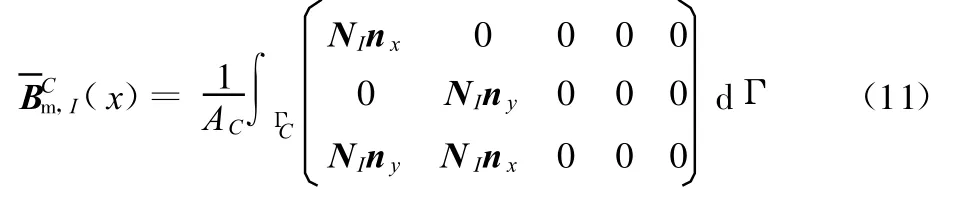
采用高斯积分对上式在光滑域 ΩC的边界ΓC上求积,得

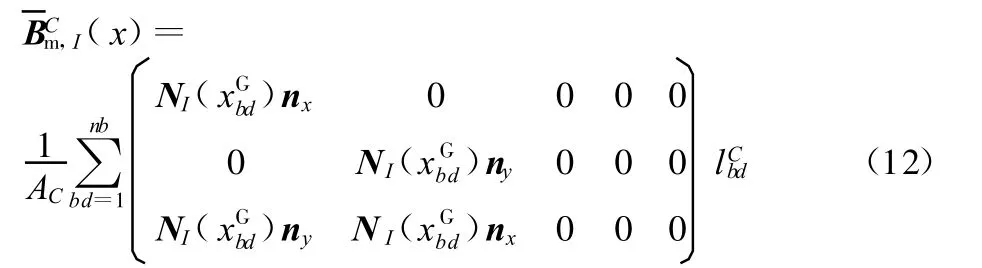
类似上面的推导,有光滑弯曲应力:

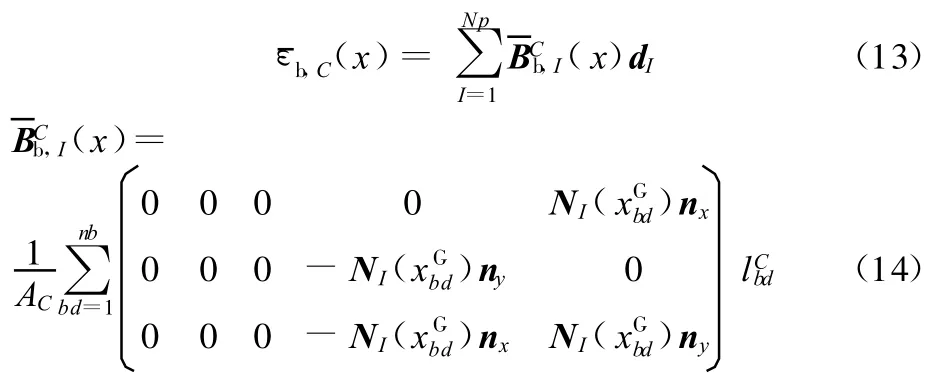
针对剪切项,剪切应变可写为

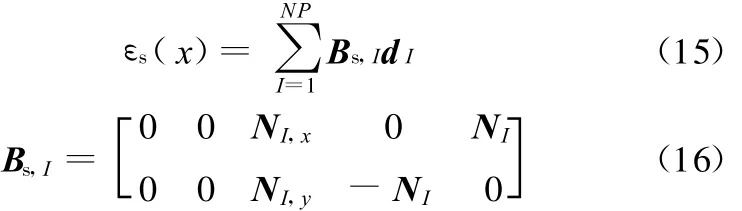
为了消除剪切自锁,本文应用MITC4单元中的办法[15]处理剪切项。不考虑结构阻尼,离散壳结构动力学方程的光滑Galerkin弱形式为

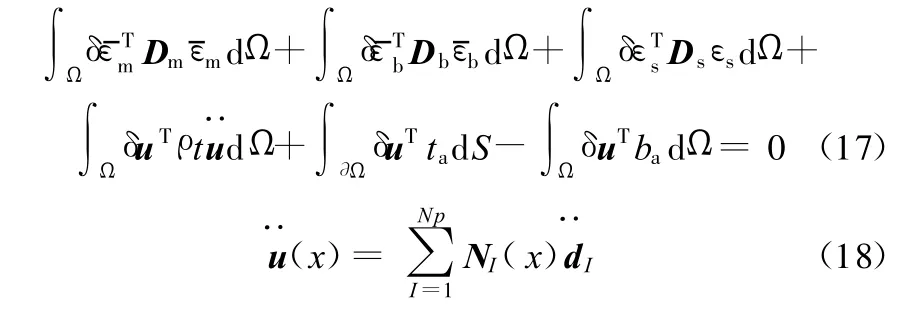
式中,ρ为材料密度;ta为表面牵引力;ba为体积力;u¨为加速度。

将式(5)、式(6)、式(9)、式(13)以及式(15)代入式(17),得壳结构离散后动力学方程:

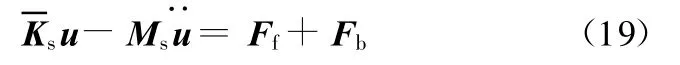
将u=Uejωt代入式(19),得频率响应分析表达式:

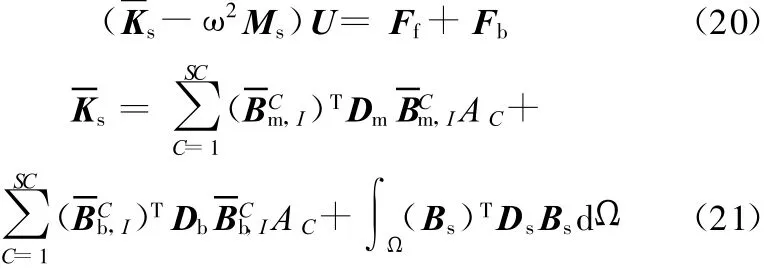
Ms采用集中质量矩阵形式表示:

入河排污口主要分布3大水系11条河流。由于各水系自然地理环境不同，经济发展程度有很大差距，工业布局在各水系差异很大，因此排污口在各水系间分布也存在相当大的差异。本次调查分布在3大水系的排污口，河北沿海诸河水系排污口最多，为20个，占排污口总数64.5%；滦河水系4个，占排污口总数12.9%；蓟运河水系7个，占排污口总数22.6%。各水系入河排污口分布情况如表2。

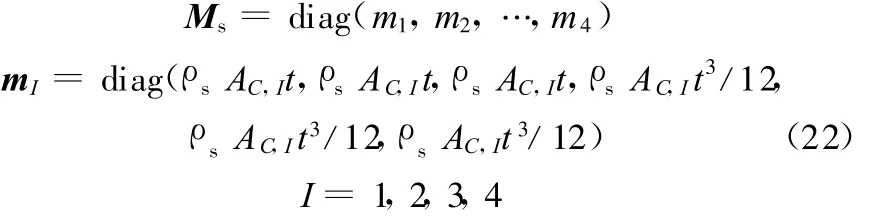
式中,AC,I为节点I相对应的第C光滑域面积;mI为节点I相对应的第C光滑域的质量矩阵;ρs为结构密度。

载荷矢量Ff和Fb可表示为

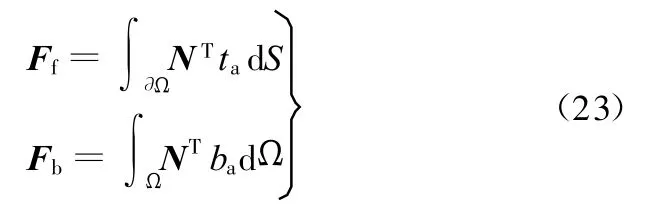
1.2 流体FEM模型

壳结构振动在理想声场介质中引起的小振幅简谐声波、声压满足Helmholtz波动方程:

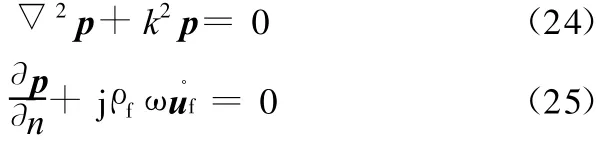
式中,p为声压;ω为圆频率;k为波数,k=ω/c;ρf为声场介质密度;u˙f为边界法向速度。

流体的伽辽金形式为

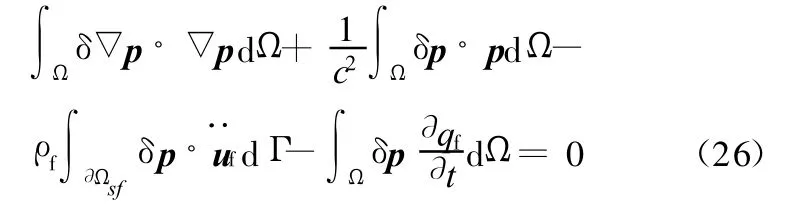
式中,qf为单位体积的附加载荷。

按照FEM方式将流体域离散为六面体网格,并采用标准的插值形函数:

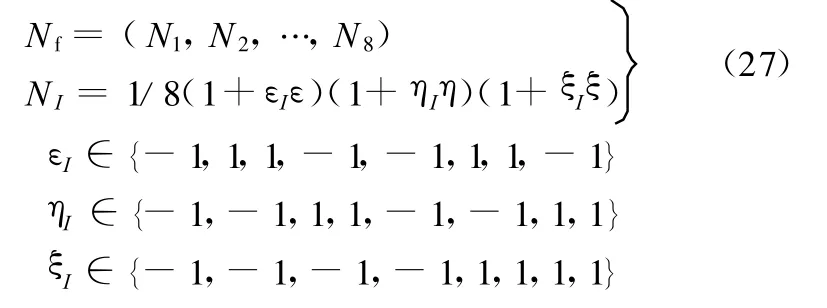
式(26)可表示为

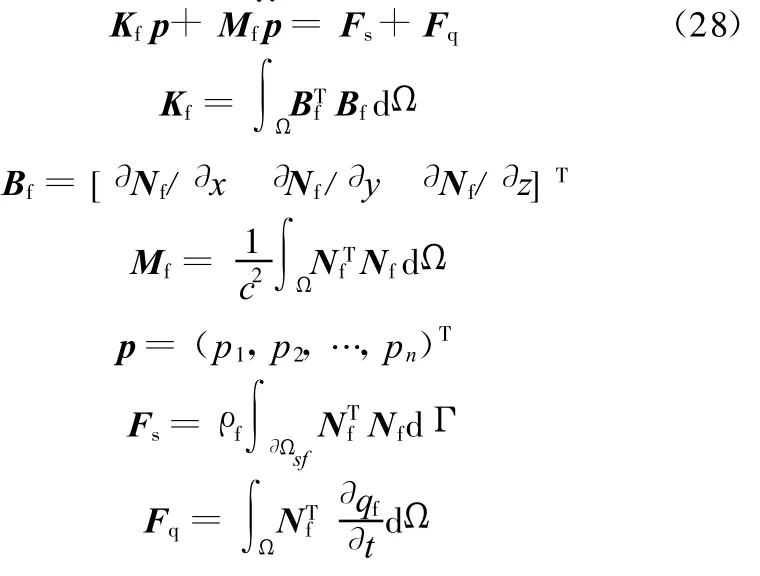
式中,Kf为声学刚度矩阵;Bf为声学梯度矩阵;Mf为质量矩阵;p为节点的声压矢量;Fs为载荷矢量。

1.3 结构—声场耦合模型

为实现结构SFEM模型和声场FEM模型耦合,在耦合界面上应满足位移和压力连续的条件[16]。引入界面法向n=nf=—ns,位移连续条件和结构应力σ与声压p的关系可表示为

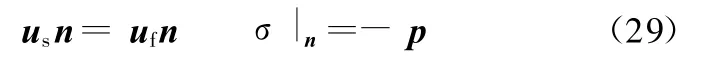
其中,nf为耦合界面声场法向矢量;ns为耦合界面壳结构法向矢量。

由式(23)可知,声场作用在壳结构耦合面Ωsf上的载荷Ff为

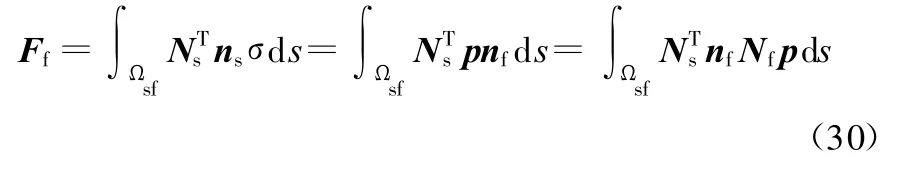
由式(28)可知,结构作用在流体耦合面 Ωsf上的载荷为

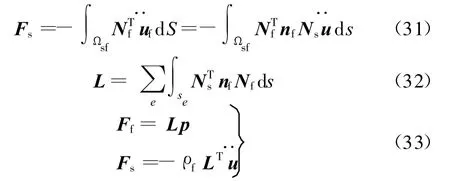
式中,L为引入耦合矩阵。

结合结构域的SFEM模型和流体域的FEM模型,壳结构耦合系统方程为

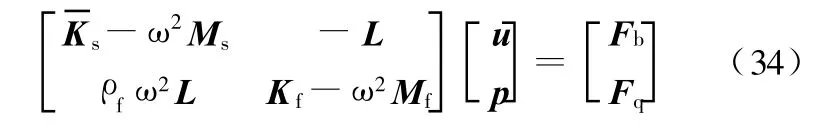
从上面的推导可以看出:在分析壳结构—声场耦合问题时,SFEM/FEM与传统的FEM/FEM[4]相似;由于SFEM/FEM在结构域分析时应用应力光滑处理技术,其计算过程相对简单,其计算结果的精度比传统的FEM/FEM高。

2 数值算例

为验证用SFEM/FEM分析结构—声场内部问题的有效性和准确性,本文分别以六面体的结构—声场耦合模型和微车声固耦合简化模型为研究对象进行分析。

2.1 六面体声场—结构耦合分析

以六面体附带矩形平面壳的结构—声场耦合模型为研究对象,如图3所示。六面体内为空气域,上表面为矩形平面壳结构,其边界角点固定约束,其他表面为刚性边界。矩形平面壳材料参数为:弹性模量E=3.0×106MPa,泊松比 μ=0.3,密度 ρs=7 800kg/m3,六面体长、宽、高均为400mm,壳结构厚度为1mm。空气声学参数为:密度ρf=1.25kg/m3,声速c=343m/s。施加在中心点+Z方向的谐波激励力幅值为1N。域点1和2为壳中心+Z方向,坐标分别为(200,200,50)mm和(200,200,100)mm。

为了评价SFEM/FEM分析结构—声场耦合问题的效果,本文计算了域点1和2的声压频率响应,频率范围为 20～220Hz,并给出了一般FEM/FEM计算结果作为对比。一般FEM/FEM是指运用传统的有限元耦合方法计算壳结构—声场耦合问题,即参考文献[4]中所提及的方法。本文中SFEM/FEM和一般FEM/FEM都是通过MATLAB程序实现,由于无法获得准确结果,本算例应用Nastran软件计算该实例高网格密度模型的近似精确解作为参考值,Nastran软件所采用的计算方法也是FEM/FEM。由于MATLAB程序与Nastran软件在计算时间上没有可比性,本文只给出了计算模型的单元数目和类型,如表1所示。

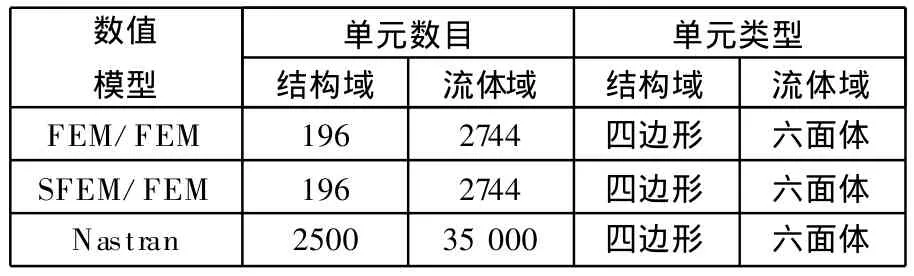
表1 模型参数

图4和图5所示分别表示域点1和2的声压频率响应曲线。其中,实线表示参考值,点划线表示SFEM/FEM的计算结果,虚线为FEM/FEM的计算结果。从图中可以看出:

(1)与FEM/FEM一样,SFEM/FEM使用网格尺寸较大模型时与参考值相差较大,但声压频率响应曲线趋势跟参考值相同。

(2)与FEM/FEM相比,SFEM/FEM的计算结果更接近参考值。这表明SFEM/FEM比FEM/FEM更精确,对粗糙网格模型的计算结果更好。

2.2 微车结构—声场耦合分析

以微车内声腔附带顶盖结构的简化模型为结构—声场耦合分析对象,如图6所示。微车内声腔为空气域,上表面为顶盖耦合面,其他表面为刚性边界无耦合。顶盖结构简化为壳结构,考虑到实际的顶盖含加强筋结构以增加顶盖刚度,结构边界角点和边缘固定约束,其材料参数为:弹性模量E=3.0×106MPa,泊松比 μ=0.3,密度 ρs=7800kg/m3,壳结构厚度为1mm。空气声学参数为:密度 ρf=1.25kg/m3,声速 c=343m/s。施加在顶盖中心点+Z方向的谐波激励力幅值为1N。

应用SFEM/FEM分析微车的结构—声场耦合问题时,驾驶员耳旁处的声压频率响应曲线是十分重要的,频率范围为20～320Hz。域点1和2分别表示驾驶员耳旁处响应点位置。应用2.1节相同的分析过程进行分析,其模型参数如表2所示。

表2 模型参数

图7、图8所示分别表示域点1和2的声压频率响应曲线。其中,实线表示参考值;点划线表示SFEM/FEM的计算结果;虚线为FEM/FEM的计算结果。从图中可以看出:对于相同网格模型而言,SFEM/FEM在分析微车结构—声场耦合问题时具有比FEM/FEM更高的精度,其结果更接近参考值。

3 结论

(1)SFEM/FEM能很好地应用于壳的结构—声场耦合分析中,其计算精度和效率比FEM/FEM要高。

(2)在分析壳的结构—声场耦合问题时,应用SFEM/FEM对结构域单元网格尺寸要求比FEM/FEM更低;SFEM/FEM计算较大网格尺寸模型时,能获得比一般FEM/FEM更高的计算精度。因此,SFEM/FEM分析壳的结构—声场耦合问题可以节约前处理分析时间,具有良好的工程应用前景。

[1]杨搏,朱平,余海东,等.基于模态分析法的车身NVH结构灵敏度分析[J].中国机械工程,2008,19(3):360-364.

[2]朱才朝,秦大同,李润方.车身结构振动与车内噪声声场耦合分析与控制[J].机械工程学报,2002,38(8):54-58.

[3]Kagawa Y,Yamabuchi T,Sugihara K,et al.A Finite Element Approach to a Coupled Structural—acoustic Radiation System with Application to Loudspeaker Characteristic Calculation[J].Journal of Sound and Vibration,1980,69(2):229-243.

[4]Davidsson P.Structure—acoustic Analysis:Finite Element Modelingand Reduction Methods[D].Lund:Lund University,2004.

[5]Everstine G C.Finite Element Formulations of Structural Acoustics Problems[J].Computer&Structure,1997,65(3):307-321.

[6]Kopuz S.Integrated FEM/BEM Approach to the Dynamic and Acoustic Analysis of Plate Structures[J].EngineeringAnalysis with BoundaryElements,1996,17:269-277.

[7]Everstine G C,Henderson F M.Coupled Finite Element/boundary Element Approach for Fluid Structure Interaction[J].The Journal of the Acoustical Society of America,1990,87(5):1938-1945.

[8]Lonny L T,Peter M P.A Space Time Finite Element Method for Structural Acoustics in Infinite Domains Part 1:Formulation Stability and Convergence[J].Computer Methods in Applied Mechanics and Engineering,1996,132(3/4):195-227.

[9]Liu G R,Nguyen T T,Dai K Y,et al.Theoretical Aspects of the Smoothed Finite Element Method(SFEM)[J].International Journal for Numerical Methods in Engineering,2007,71(8):902-930.

[10]Liu G R,Dai K Y,Nguyen T T,et al.A Smoothed Finite Element Method for Mechanics Problems[J].Computational Mechanics,2007,39(6):859-877.

[11]Cui X Y,Liu G R,Li G Y,et al.A Smoothed Finite Element Method(SFEM)for Linear and Geometrically Nonlinear Analysis of Plates and Shells[J].Compute Modeling in Engineering&Sciences,2008,28(2):109-125.

[12]Dai K Y,Liu G R.Free and Forced Vibration AnalysisUsing theSmoothed FiniteElement M ethod(SFEM)[J].Journal of Sound and Vibration,2007,301:803-820.

[13]Nguyen X H,Rabczuk T,Stephane B,et al.A Smoothed Finite Element Method for Plate Analysis[J].Compute Methods Applied Mechanics and Engineering,2008,197(13/16):1184-1203.

[14]Nguyen T N,Rabczuk T,Nguyen—Xuan H,et al.A Smoothed Finite Element Method for Shell Analysis[J].Computer Methods in Applied Mechanics and Engineering,2008,198(2):165-177.

[15]Bathe K J,Dvorkin E N.A Four—node Plate Bending Element Based on Mindlin/Reissner Plate Theory and a Mixed Interpolation[J].International Journal for Numerical Methods in Engineering,1985,21:367-383.

[16]Fredrik H.Structure—acoustic Analysis Using BEM/FEM[D].Lund:Lund University,2001.