石雕椭圆形廓多轴联动磨削的数学模型

陈为旭 张济宇

福州大学,福州,350002

0 引言

由于石材特性及需要不同造型的特殊性,石雕型面加工中需用多轴联动加工设备[1],这与金属切削机床有本质的不同。石材多以切边、切片、平面磨光及笔式雕刻等类型为主,大多采用PLC控制器和变频器,以驱动变频电机为主要控制结构,且雕刻机所配置的数控系统中联动轴数少,不易实现复杂型面的自动加工;同时控制系统提供给用户的一般只有直线和圆弧插补指令,在加工复杂曲线时,需对复杂曲线进行分段,采用小段直线插补或圆弧插补等指令进行循环逼近[2],会出现数控代码量增大、逼近精度差及加工速度受限等问题而无法实现复杂石材型面的批量生产[3]。在一些进口的多轴联动石材设备中,可结合CAD型面造型软件来设计石材型面及加工出复杂石雕产品,但目前仅在少数企业中得到应用,由于该设备价格昂贵,又没有提供四轴以上的多轴联动编程技术,在实际应用中效果不佳。

本文基于国产的石材加工设备,通过电气控制结构的改造分析,建立五轴联动控制系统[4],对复杂型面进行椭圆曲面的插补拟合,同时采用大规格切片磨轮,通过控制磨片的空间相对位置,形成椭圆磨削形廓,设计形廓中心的空间运动轨迹,导出多轴联动复杂运动的数学模型,使磨片包络出各种不同的椭圆型面,并拟合出复杂石雕型面,最终有效地实现了复杂型面的自动加工,提高了精度和效率。

1 多轴联动石雕磨床的系统结构分析

我国当前的石材加工仍属于劳动密集型产业,设备的控制系统通常不能多轴联动,一般只能实现切边、磨面及笔式雕刻等操作。本文基于国产QSJ改进型石材自动桥式切机,对其机械、电气和软件进行分析、改进,构成五轴联动控制系统,以实现复杂型面的自动加工。

1.1 机械结构分析

图1所示为QSJ改进型石材加工设备,具备五轴联动控制的结构功能。

石雕工件固定在工件回转台1上,沿着垂直立轴在水平面上做C轴回转。金刚石圆磨片2安装在水平磨削主轴3上,沿着垂直立轴在水平面上做B轴回转。水平磨头4沿着立轴做y轴的上下直线运动。立轴联同磨头沿着横梁导轨5做纵轴x的左右直线运动。横梁联同立轴和磨头沿着左右横向支架导轨6做横轴z的前后直线运动。

根据石雕形廓的曲率大小,选用相应直径的金刚石磨片,根据曲率吻合原则[5],回转B轴,使磨片与工件的曲率吻合,控制x、y、z及C轴,通过五轴联动,可最大效率地加工出石雕复杂形廓。

1.2 电气控制结构分析

图1所示石材设备的原型设计的控制系统是采用PLC控制器来控制变频器的,以驱动变频电机为主要结构,结合型面磨轮,常用于加工直线型、回转型曲面,虽具有五轴控制结构,但联动轴数少,无法实现精确的多轴联动控制。

现对该设备进行五轴联动控制结构改造,采用工控微机,通过PCI接口,连接伺服电动机的运动控制卡,经过伺服控制器,驱动伺服电动机及联轴器,这一五轴联动电气控制结构框图如图2所示。

复杂型面可在工控微机上用造型软件生成[6],也可采用数控代码进行编辑设计,然后执行加工指令,产生数控指令,通过运动控制卡,发出伺服电动机的控制指令,经过驱动器的闭环控制,驱动伺服电动机作伺服运动,经过联轴器驱动滚珠丝杆,实现 x、y、z轴的直线运动;此外,电动机经过联轴器驱动蜗杠蜗轮实现B、C轴的回转运动,从而构成五轴联动。

1.3 软件设计分析

首先,在工控微机上安装曲面造型CAD软件[7],通过NURBS曲面[8]来体现曲面形状[9]及实现复杂石雕型面的造型设计,进一步求出复杂型面的型值点,采用椭圆线段对型值点进行椭圆曲面拟合,产生椭圆拟合线段,并得出每一椭圆线段的离心率参数。

然后,依据椭圆线段的离心率参数,选用相应直径的金刚石磨片,并确定其在B轴上的回转角度,如此可使磨片的有效切削形廓也为椭圆形廓,设计并给出金刚石磨片回转中心的运动轨迹,使其有效切削形廓,包络出工件上的椭圆曲线,实现工件椭圆线段精密和高效的磨削加工。

显然,金刚石磨片回转中心的运动轨迹是一个非常复杂的运动曲线,为此,本文将其作为设计与推导的重点内容。

2 石雕椭圆廓面数控磨削的位置关系

2.1 石雕廓面椭圆拟合算法分析

为了加工图3所示的复杂动物雕像或龙柱柱体等工件,一般首先采用CAD造型软件,设计其形廓,采用多边形建模方式为主,辅以曲面造型技术,设计出图4所示的网格图。

从图4可以看出,石雕形廓中包含着许许多多的复杂曲线,一般由样条曲线构成,样条曲线上包含着确定曲线特征的型值点。如果采用常规的小段直线或圆弧拟合这些样条曲线,则拟合量大且精度差。现沿着x轴方向,以给定步长Δx对复杂形体进行逐步切片,则可形成如图5所示的切面集合,且每一切面的外廓曲线上包含着一系列的型值点。

采用椭圆曲线拟合每一切面的外廓曲线,有多种算法,如基于 HOUGH变换的椭圆拟合方法,基于不变矩方法和基于最小二乘法等[10]。在平面坐标中,根据椭圆中心点坐标(y0,z0)、椭圆长轴的旋转角度θ、半长轴p及半短轴q这5个参数可以确定一个椭圆,该椭圆的方程可以表示为

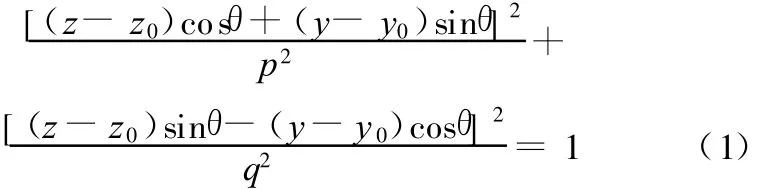
根据切面上样条曲线上相邻的5点,将其坐标(yi,zi)代入式(1),即可求出 y0、z0、θ、p、q这 5个参数值,从而确定该5个样本点拟合的椭圆曲线。拟合算法如下:

(1)从起始点p1开始,取出相邻的5个型值点,分别代入式(1),得到联立方程组,求解y0、z0、θ、p、q这5个参数值,如求出的参数值为实数,则拟合成功,转入(3);如求出的参数值含有虚数,则转入(2),进行纠正处理。

(2)在公差允许的范围内,分别调整5个型值点的坐标值,直到求出的 y0、z0、θ、p、q这5个参数值为实数值止;如不能成功,则需丢弃第5个型值点,另在前4个型值点中增加一个样本点,按(1)求解拟合椭圆曲线。

(3)采用代数距离法,将后续的型值点逐个代入拟合出的椭圆方程内,检测其误差,若代数距离小于指定的公差值,则确定该后续的型值点位于所拟合的椭圆线段内,予以丢弃,直到代数距离超出公差为止。

(4)若代数距离大于指定的公差值,则取其前相邻的一个型值点和其后相邻的3个型值点,组成5个型值点,按照(1)进行下一椭圆线段的拟合处理,直到终点结束。

讨论1:代数距离[11]不同于实际的几何距离,以代数距离确定精度存在一定的误差,但在石材粗加工中,精度要求不是很高,通过确定代数距离的量级水平,可以满足要求。

讨论2:对于局部细小形廓,型值点密集,会遇到拟合的椭圆曲率半径太小,难以实现加工。因此,先忽略局部细小形体结构,这些结构可通过后续精加工工序,采用小型刻刀切出,以便于提高粗切效率。

对于复杂石雕雕像的形体结构,通过多条椭圆曲线的拟合后,就构成了不同离心率的椭圆曲线的集合。

2.2 多轴联动数控磨削的位置关系分析

在分析出复杂形体的椭圆曲线集合后,即可选用相应的磨片直径,控制B轴转角,使磨片位于相对于工件的椭圆曲面,其相对位置示意如图6所示。

磨片操作时,先控制x、y、z轴联动,使磨片的椭圆形廓包络出工件上的椭圆形廓,以实现高效精确的型面加工。在磨片强度和加工余量许可的条件下,通过控制进给速度,或控制B、C两回转轴参与联动,来实现复杂的五轴联动轨迹控制。

3 石雕椭圆廓面的多轴联动磨削的数学模型设计

如上所述,回转B轴,控制磨片转角,形成椭圆形的磨片形廓,实现不同的有效磨削点曲率,用于包络工件复杂的椭圆型面,可最大限度地满足曲率吻合原则。但在磨削的包络过程中,有效磨削点沿着磨片椭圆面上连续变动,因此磨片的空间位置,也就是磨片中心点的空间坐标,也要随之进行相应的调整,才能确保变动的磨削点在工件上磨出椭圆形廓。为此分析磨削点的运动轨迹,进而得出描述磨片中心点控制轨迹的数学模型是首要的关键。

3.1 磨削点的运动轨迹分析

磨削点的运动轨迹,也就是最终在工件上包络出的轨迹,对于石雕椭圆廓面来说,其轨迹就是椭圆曲线,如图7所示。

设定通用的磨削点的初始位置为P0(x0,y0,z0),沿着椭圆曲线P0PiPe,运动到终点Pe(xe,ye,ze),则其动点Pi(xi,yi,zi)的坐标为

式中,t为磨削点Pi在曲线P0PiPe于 yz平面上的投影椭圆曲线上的离心角(t=0～ 90°);s为磨削点 Pi在曲线P0PiPe于xy平面上的投影椭圆曲线上的离心角(s=0 ～ 90°)。

为了磨削出椭圆曲线P0PiPe,需要控制磨片的相对位置。

3.2 磨削切片与石雕工件相对位置的数学模型

磨片与石雕工件的相对运动如图8所示,基于本文设计的五轴数控磨床在加工椭圆曲线P0PiPe时有如下关系:

(1)将石雕工件曲线P0PiPe的椭圆中心作为磨床的相对坐标原点O,设定磨削点坐标为Pi(xi,yi,zi),则 xi,yi,zi应满足式(2)～ 式(4)。

(2)磨削砂轮沿B轴回转,直到磨削面贴合待磨石雕的表面,为避免干涉,必要时可留出1°～2°的磨削后角。当砂轮转过 b角度后,在 xy平面上的投影也是椭圆,其中心为Oi(x,y,z),因此,从砂轮中心Oi至磨削点Pi在z轴方向上的距离Wp,及在y轴方向上的距离Wq和在x轴方向上的距离Ww应满足如下关系:

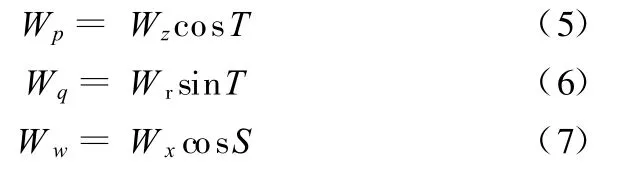
式中,Wz为砂轮中心与起始磨削点在z向上的距离;Wr为砂轮半径;Wx为砂轮中心与起始磨削点在x向上的距离;T为磨削点Pi在砂轮于yz平面上投影椭圆Oi上的离心角(T=0～ 90°);S为磨削点Pi在砂轮于xy平面上的投影椭圆Oi上的离心角(S=0～ 90°)。

(3)石雕工件沿C轴回转,仅用于回转形工件表面的磨削运动,因此在讨论椭圆曲线P0PiPe的磨削运动时,不参与联动。

当横轴z沿横向运动,使砂轮中心坐标从z=z0+Wz运动到z=0位置(其中,z0是椭圆形曲线P0PiPe的起始磨削点在z向的坐标),这时立轴y与z联动,可使砂轮的包络面吻合椭圆曲线P0PiPe,同时砂轮中心的纵坐标将从y=0运动到y=ye+Wr(其中,ye是椭圆形曲线P0PiPe的终点在y向的坐标)。则y与z的联动关系可从图6导出,当砂轮运行到磨削点Pi时,砂轮中心坐标Oi(x,y,z)应为

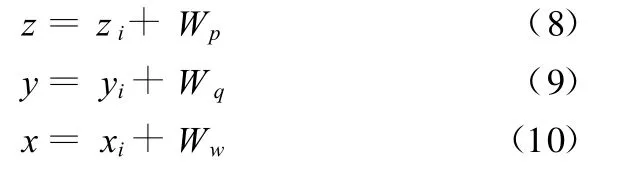
(4)首先在yz平面上考察砂轮投影椭圆与工件椭圆曲线的相对位置关系,由于工件形廓是由磨片椭圆形廓包络形成,所以椭圆Oi与椭圆曲线P0PiPe相切,则有

将式(2)、式(3)、式(5)、式(6)代入式(11),得

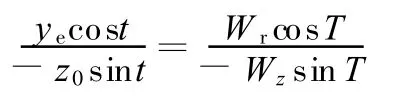
于是有

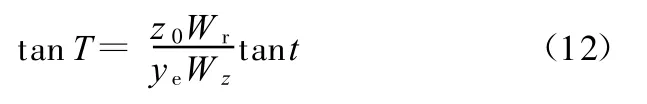
式(5)经变换得

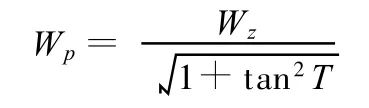
将式(12)代入上式,有

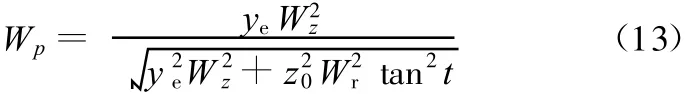
将式(13)及式(2)一并代入式(8)后,有

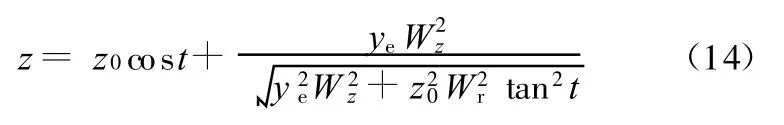
同理,变换式(6)得出

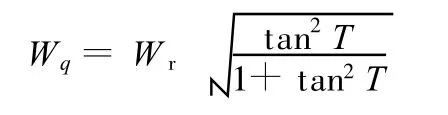
也将式(12)代入上式,有

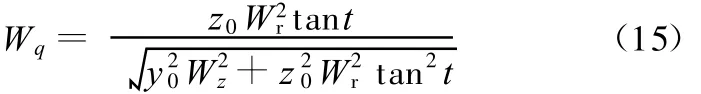
将式(15)及式(3)一并代入式(9)后,有

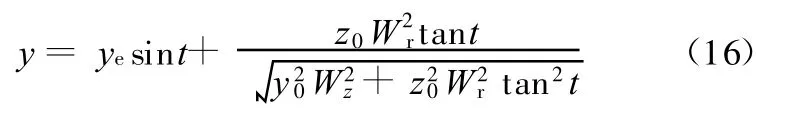
(5)在 xy平面上考察砂轮投影椭圆曲线与工件椭圆曲线的相对位置关系,由于此时砂轮的形廓椭圆与工件的形廓椭圆不一定相切,且砂轮磨片的形廓与厚度不同,均会产生不同程度的磨削干涉,这时需要通过调整B轴来改变砂轮摆角以避免干涉。

同样,从图6中的xy平面中可以得出:

比较式(17)与式(3),有

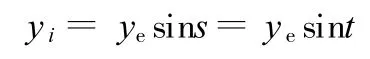
由于s与t为同一磨削点在所形成的椭圆轨迹上的离心角,且s与t的取值均限制在0～ 90°范围内,可知s与t相等。于是,式(4)变为

对图6中xy平面上的砂轮形廓有

比较式(19)与式(6),有

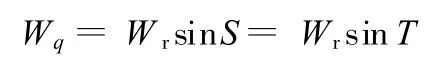
由于S与T均限制在0～90°范围内,可知其对应的砂轮上的磨削点的离心角也应限制在0～90°范围内,所以 S=T,代入式(6)后,得出:

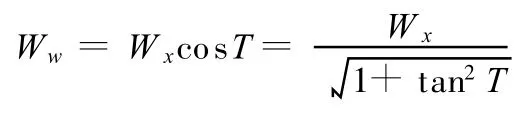
将式(12)代入上式后,有

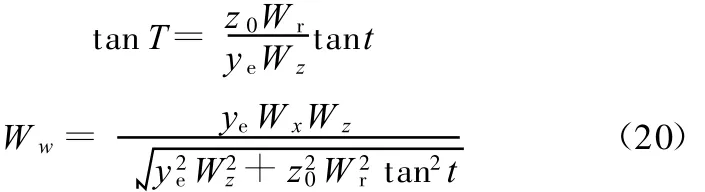
将式(20)及式(18)一并代入式(10)后,有

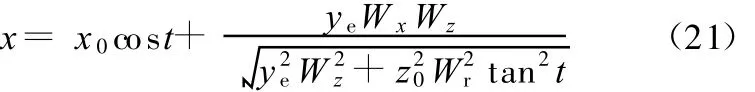
至此,式(14)、式(16)、式(21)构成了磨削椭圆形曲线在P0PiPe时x、y、z的联动曲线关系,也即磨削椭圆曲线的三直线轴联动的数学模型,在切削条件允许状态及精磨要求磨削量较小时,配合砂轮B轴的回转及工件C轴的回转运动,构成了一个五轴联动的控制模式,实现了加工相应复杂型面的目的。

需要指出的是,该五轴控制系统的多轴联动控制模型是与椭圆曲线的离心角相关的复杂的曲线关系,离心角取值不同,可实现不同线段的控制。在进行插补控制时需要采用必要的逼近措施,即选用合适的插补算法[12]以实现联动控制。

4 测试

基于本文提出的五轴联动控制模式,在QSJ改进型石材自动桥式切机上进行了如图3所示的实际石雕工件复杂型面的磨削测试,过程如下:

(1)毛料及原始参数。选用花岗石毛料,牌号G687,莫式硬度为6.9,原始尺寸的长×宽×高为1600mm×400mm×1200mm;切削刀具为金刚石切片,粗切刀具尺寸为φ 600mm×4.6mm,精切刀具尺寸为 φ 200mm×2.6mm;粗切速度为 5 m/min(辅以手动调速,以防石材破裂),精切速度为1m/min。

(2)曲面造型,设计石雕形廓。采用CAD造型软件,先设计出图3所示马的形廓,目标尺寸长×宽×高为1523mm×312mm×1088mm,然后再生成图4所示的网格图。

(3)以纵向增量 Δ x=15～20mm为步长,在总长为1523mm的长度方向上共切出90个切面,参考图5,采用本文提出的算法分别对每一个切面外廓曲线进行椭圆拟合,计算出每一椭圆拟合线段连接点的坐标值。以第31个切面为例,切出的切面如图5所示,拟合出的椭圆线段连接点的坐标是:Pi(yi,zi)=[(950.462,0.000);(943.594,—23.486);(878.824,—105.616);(813.850,—105.616);(775.989,—120.098);(731.426,—126.582);(698.348,—128.318);(675.331,—134.001);(619.339,—143.476);(550.709,—132.801);(538.622,—126.881);(523.724,—124.348);(467.829,—118.532);(414.876,—103.187);(369.509,—89.277);(321.340,—86.949);(297.693,—90.778);(271.635,—89.666);(210.703,—76.837);(127.153,—83.312);(106.370,—84.151);(83.578,—79.427)]。

i=1,2,…,22,即用 22个型值点,共12段椭圆弧,拟合出高为950.462mm的第31个切面上左半边样条曲线,其右半边与之对称,采用对称功能即可实现加工。

(4)根据每一椭圆拟合线段的起止坐标,分别计算出各椭圆线段的离心角t。

(5)选用相应的磨削切片,调整 x、y、z、B 、C五轴的初始位置。B、C两轴根据实际曲线形状和控制参数参与联动进给。

采用式(14)、式(16)、式(21)计算出磨削切片中心点相对于工件的运动轨迹坐标,并配合参数曲线插补控制算法[12],使磨片的椭圆运动轨迹的磨削点包络出工件上的椭圆轨迹。

具体切削过程包括:粗切→去毛料→精切→局部精雕→抛光等工序。

粗切后的工件如图9所示。精切抛光后的成品如图3所示。测试结果对比如下:

(1)当采用传统的人工雕刻技术来完成图3所示1m高的工件雕像时,不包括图纸设计绘制时间在内,人工雕刻至少需两人两周时间,即人均1个月时间才能完成。

(2)采用本文设计的五轴联动自动桥式磨切设备加工时,不包括CAD形体编程设计的时间在内,仅需1人两天即可完成。

相比而言,采用本文研究的加工技术后,效率大幅提高,更重要的是确保了重复精度和降低了粗磨误差,减轻了劳动强度,提高了加工自动化技术水平,改善了操作人员的劳动条件与环境。

5 结束语

对类同于国产QSJ改进型石材自动桥式磨切设备,均可通过结构改造,建立五轴联动的数控系统。应用CAD造型软件,设计复杂石雕型面,得出型面的网格结构,分析出每一切面的型值点。根据复杂型面的型值点,结合曲面造型拟合出的样条曲线上的样本点,采用本文提出的椭圆拟合算法,进行复杂石雕工件的椭圆曲面拟合,得出拟合椭圆线段集合。根据本文推导出的五轴联动数学模型及控制模式,实现了磨片上椭圆形磨削轨迹包络出石雕型面上的椭圆曲线,实际测试证明该椭圆拟合技术能实现复杂型面高效精确地磨削加工。

[1]Luo Jiman,Xing Yan,Wang Dan,et al.New Type Parallel RobotManipulatorofStone Machining[C]//Proceedings of the IEEE International Conference on Automation and Logistics.Qingdao:IEEE,2008:2417-2419.

[2]Yong T,Narayanaswami R.A Parametric Interpolator with Confined Chord Errors,Acceleration and Deceleration for NC Machining[J].Computer—aided Design,2003,35:1249-1259.

[3]王宇晗,肖凌剑,曾水生,等.小线段高速加工速度衔接数学模型[J].上海交通大学学报,2004,38(6):901-904.

[4]Zhong Yunqing.Design on Mechanical System for Optimal Cutting Movement Trajectory of High—efficacy Stone—sawing Mchinine[C]//2007 IEEE International Conference on Control and Automation.Guangzhou:IEEE,2007:621-624.

[5]倪炎榕,马登哲,张洪,等.圆环面刀具五坐标数控加工复杂曲面优化刀位算法[J].机械工程学报,2001,37(2):87-91.

[6]韩福柱,程刚,陈希明,等.电火花线切割加工自由曲面的CAD/CAM软件[J].清华大学学报,2005,45(11):1472-1475.

[7]黄国钦,谢明红,徐西鹏.圆锯片数控加工异性石材线条的自动编程系统开发[J].金刚石与磨料磨具工程,2005,148(4):33-37.

[8]Chiou J C J,Lee Y S.Five—axis High Speed Machining of Sculptured Surfaces by Surface—based NURBS Path Interpolation[J].Computer—aided Designed and Applications,2007,4(5):639-648.

[9]Lei W T,Sung M P,Lin L Y,et al.Fast Real—time NURBS Path Interpolation for CNC Machine Tools[J].International Journal of Machine Tools&Manufacture,2007,47:1530-1541.

[10]闫蓓,王斌,李媛.基于最小二乘法的椭圆拟合改进算法[J].北京航空航天大学学报,2008,34(3):295-298.

[11]雷志术,张雁波.椭圆定形曲线拟合问题若干新型算法[J].上海交通大学学报,2002,36(8):1210-1213.

[12]游有鹏,王氓,朱剑英.参数曲线的自适应插补算法[J].南京航空航天大学学报,2000,32(6):667-671.