临坡条形基础极限承载力上限计算*

赵炼恒 罗 强 杨 峰 李 亮 但汉成

(中南大学土木建筑学院1) 长沙 410075) (贵州省交通运输厅基建处2) 贵阳 550003)

地基基础承载力分析是岩土工程中的经典问题[1-2].浅基础临近边坡,直接将浅基础置于边坡上,或既有建筑物浅基础一侧进行基坑开挖施工时,与水平地基不同,斜坡的存在必然对地基承载力有削减,其破坏模式也将有所不同[3-6].同时已有研究表明边坡存在将导致地基承载力减损,但折减的程度及规律尚需要研究和探讨.

本文根据线性破坏准则和相关联流动法则,利用极限分析中的机动法,构建了一个边坡基础极限承载力的二维机动许可破坏模式.根据能耗相等原理获得极限承载力的约束表达式,并把其转化成了一个求含有非线性约束的最小值问题计算模型.通过编写程序,对计算模型采用序列二次规划法(SQP法)[7]进行了优化求解.研究结果与已有资料进行了对比,并对影响斜坡地基承载力的部分参数进行了敏感性分析.

1 刚性块平动破坏机制

1.1 破坏机制

条形基础宽B,边坡倾斜角度 δ,边坡上承受均布外荷q,假设基础与地基不出现相对滑动,并假设临坡条形浅基础在极限承载力P u作用下,地基土出现单侧平动破坏,破坏机制由(n+1)个三角形刚性块组成,未知参数 θ1,θ2,αi,βi 决定三角形刚体形状,进而决定破坏机制和速度场.如图1,图2所示.

根据图1,由三角形简单的几何关系可计算各三角形边长LAC,B1,D i,Li及面积Si(i=1,…,n).

根据图2,由相容速度闭合的三角形几何关系可计算各速度间断线D i和L i上的速度Vi和Vi-1,i(i=1,…,n).

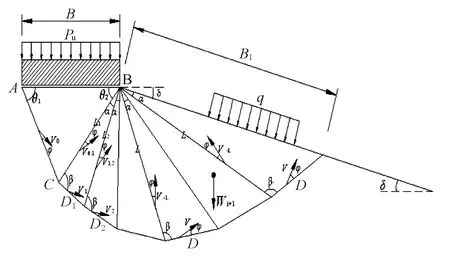
图1 临坡条基平动破坏机制及受力分析

1.2 能耗计算

能耗计算包括外力做功和内部耗能两方面.

图2 相容速度三角形

由图1～2可知,在极限承载力的作用下,外力的功率为:极限承载力Pu的功率WPu,条基下方三角形土重力的功率WABC,条基临坡一侧n个三角形刚块土体重力的功率W soil,边坡表面均布荷载q所做功率Wq.

条基为刚性基础,基础下土体为理想刚体,无塑性变形,单侧破坏模式的内部耗能发生在速度间断线上,包括Di,Li(i=1,…,n)上的内部耗能∑Gi和∑Qi.另外,刚体ABC与一侧土体的速度间断线AC上亦有能量耗损GAC.

利用虚功率原理,根据破坏模式中外力所做功率与内部耗能相等,将各能量计算式代入式(2)建立起极限承载力P u的计算表达式(3)有

在式(2)中,B,γ,q,φ,c都是已知量,极限承载力P u 仅与未知参数 θ1,θ2,αi,βi(i=1,…,n)有关 .即所有的三角形单元几何参数,对于本文中含有k(k=n+1)个三角形刚体的单侧破坏机构而言共有2k个变量.很显然,这些自变量应满足平动机制三角形刚体运动协调的速度场约束条件和物理意义要求的几何约束条件.

工程中,Terzaghi地基承载力分项表达式被普遍使用.

式中:Nc,Nq和Nγ分别代表临近基坑土体黏聚力c,超载q和土体自重γ的影响系数.

2 SQP优化方法与实现

由以上分析可知,对于不同的自变量甚至是自变量组合,利用式(3)能得到不同的极限承载力上限解.但极限分析上限解总是大于真实极限荷载的,所以在上限解中越小的值则越接近真正的极限荷载值,则对以上上限分析的求解实际上转化成了一个获求含非线性约束的最小值问题.序列二次规划算法(简称SQP法)适用于非线性较严重的问题.已有研究表明[8],对这类包含自变量θ1,θ2,αi,βi(i=1,…,n)约束条件和目标函数极值Pu的非线性函数,SQP法能够获得颇好的效果.

利用MATLAB软件平台,采用SQP法对该问题上限解进行了优化,15个刚性块极限承载力平动破坏模式SQP优化结果如图3所示.其中,边坡角 δ分别等于10,20,30°;岩土内摩擦 φ=30°.其他参数满足:c/(γB)=0.5;q/(γB)=0.25.

图3 破坏机构优化结果

由图3可看出:在其他参数一定的情况下,边坡倾斜角度的增加将使地基破坏区域发生显著变化,因而边坡角度变化对条形基础临坡地基极限承载力的影响会很大.

3 数值计算对比与影响参数分析

3.1 计算精度控制

研究表明[8],极限上限分析中,刚性块体划分个数对结果的精确性和优化效率的影响均较大.当B=2m,φ=25°,δ=150,c=20 kPa,q=10 kPa,γ=20 kN/m3,划分为不同刚性块体数量时,对极限承载力值P u的最优结果的影响如图4所示.

由图4知:随着刚性块的增多,P u将逐步减小并趋向于精确的解,且这种减小趋势的变化率是迅速减小的.对于相同的计算参数,当刚性块数量超过50个,刚性块增多所得的P u量值变化很小.

图4 P u随刚性块个数变化情况

3.2 对比计算

本文计算结果与文献[1-2]给出的极限承载力分项系数Nγ值的最小计算值结果进行对比如表1.其中:Siva采用滑移线法;M eyerho f和M izuno采用极限平衡法;Chen,Saran采用了极限分析上限法.

表1 N r计算与已有结果对比

由表1中的结果对比看出:采用极限分析上限法本文所得 Nγ值较Chen,Saran的结果小,是较好的上限解;与Siva的滑移线法以及Meyerhof和Mizuno的极限平衡法所得的 Nγ值也比较接近.进而可以证明本文方法和编写程序的正确性.

3.3 影响参数分析

承载力分项系数 Nc,Nq已有公认的解析表达式,而Nγ尚未获得真实解.限于篇幅,以下主要分析内摩擦角φ和边坡倾角δ对Nγ,Nc,Nq的影响.

3.3.1 内摩擦角对承载力分项系数影响 固定边坡倾角δ而岩土体内摩擦角φ变化,假设条基宽B=2 m且速度相容机构划分为50个刚性块体时,分别Nγ,Nc,Nq系数值进行优化求解如图5所示.δ和φ同时变化对各系数的影响如图6所示.

由图5看出:坡角δ不变的情况下,岩土体内摩擦角φ数值增加对极限承载力分项系数Nγ,Nc,Nq的量值影响具有较强的非线性增加趋势.

结合图3,由图5和图6可知:岩土体内摩擦角φ提高使各分项系数迅速增大,因而地基极限承载力显著提高,而边坡的存在对临坡地基承载力存在较大的不利影响,且破坏区域亦将发生显著变化.

3.3.2 边坡倾角对承载力分项系数影响 固定岩土体内摩擦角φ而边坡倾角δ变化,假设条基宽B=2m且速度相容机构划分为50个刚性块体时,分别Nγ,Nc,Nq系数值进行优化求解如图7所示.δ和φ同时变化对各系数的影响如图8所示.

图5 Nγ,Nc,Nq随φ变化情况

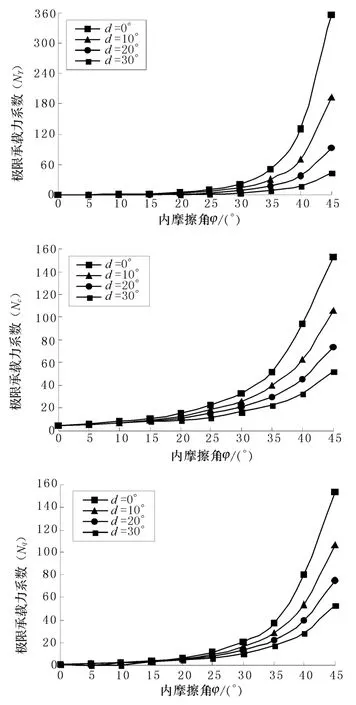
图6 Nγ,Nc,Nq随φ变化情况

由图7可见,在岩土体内摩擦角 φ一定的情况下,边坡坡角增加对极限承载力分项系数的量值影响具有较强的非线性减小趋势.

图 7 Nγ,Nc,Nq随δ变化情况

图 8 Nγ,Nc,Nq随δ变化情况

结合图3,由图7和图8知:边坡倾角的增加将使地基破坏区域发生显著变化,使各分项系数呈非线性趋势迅速减小,地基极限承载力显著降低.边坡的存在对临坡地基稳定性存在较大的不利影响,而岩土体内摩擦角 φ提高将对提高地基承载力有利.因而在实际工程应用中,可通过改良地基土物理力学特性或减缓边坡坡角来提高基础稳定性.

4 结 论

1)计算中随着刚性块的增多,极限荷载将逐步减小并趋向于精确的解,且减小趋势的变化率是迅速减小的.相同计算参数条件下,构造刚性块较少的简单相容速度场也能够求得较为精确的数值,因而计算的速度和效率也将得到大幅提高.

2)边坡倾斜程度和地基岩土体内摩擦角 φ对临坡条形基础地基承载力影响较大.边坡坡角δ的增加将使地基破坏区域发生显著变化,使极限承载力各分项系数Nγ,Nc,Nq迅速减小,地基极限承载力将减小;而内摩擦角 φ增加对 Nγ,Nc,Nq的影响恰恰相反.因而在实际工程应用中,可通过改良地基土物理力学特性或减缓边坡坡角来提高基础稳定性.

3)将计算结果与已有文献资料比较分析表明,所得结果较前人研究成果有一定改进.

[1]Saran S,Sud V K,H anda SC.Bearing capacity o f footings adjacent to slopes[J].Journal of Geotechnical Engineering,1989,115(4):553-573.

[2]酆庆增.临近边坡的基础的极限承载力[J].力学季刊,1999,20(1):24-27.

[3]王红雨,杨 敏.临近基坑条形基础地基承载力简化上限解[J].同济大学学报:自然科学版,2006,34(3):319-324.

[4]Yang X L,Wang Z B,Zou JF,etal.Bearing capacity o f foundation on slope determ ined by energy dissipationmethod andmodel experiments[J].Journalof Centra l South University of Technology,2007,14(1):125-128.

[5]赵 杰,邵龙潭.土体结构极限承载力的有限元分析[J].岩石力学与工程学报,2007,26(增刊1):3183-3189.

[6]李耘宇,胡晓敏,张嵘峰.地震液化对桥梁桩基础极限承载力的影响[J].武汉理工大学学报:交通科学与工程版,2006,30(6):1044-1047.

[7] 赵炼恒,李 亮,杨 峰,等.基于SQP和上限法的非饱和土条形基础极限承载力计算[J].岩石力学与工程学报,2009,28(增刊1):3021-3028.