全液压十一辊矫直机矫直力的计算

杨晓君 王效岗 王树环

全液压十一辊矫直机矫直力的计算

杨晓君 王效岗 王树环
(太原科技大学，山西030024)

从研究矫直原理入手，根据弹塑性弯曲理论，利用曲率积分理论，得出了矫直力的计算方法。

十一辊矫直机；矫直力；计算

矫直作为一种精整技术，其重要性日益突出，已成为工业发展不可或缺的分支。尤其近年来，世界各国对产品质量和精度的普遍重视，使得矫直技术迅猛发展。矫直机已经成为轧制车间必不可少的重要设备。

但是目前在国内矫直设备的设计制造上，由于矫直理论和技术水平的限制，对变形中的板材形态研究不足，导致存在着设计矫直力大于实际矫直力、矫直机整体自控水平低等问题，不能充分发挥矫直设备的实际矫直能力。本文就是基于十一辊全液压矫直机试验平台的建设，利用曲率积分理论[1，2]，考虑矫直过程中矫直辊与板材之间的接触点所处的位置及相互之间的距离对板材弯曲的影响，建立符合矫直变形规律的变形曲线，从而精确计算矫直力及矫直辊压下量，以确保产品的质量和精度。

1 传统矫直力计算方法

矫直机工作辊上受力简图如图1所示。

弹性弯曲力矩MW=bh2/6×σs，弹塑性弯曲力矩MS=bh2/6×σs。

式中，b为宽度；h为高度；σs为屈服极限。

假设各辊子处在轧件断面的弯矩分配方案为：

图 1 作用在矫直辊上的压力Figure 1 Pressure acting on straightener roll

M2=M3=M4=MS(塑性)

Mn-3=Mn-2=Mn-1=MW(弹性)

M5=M6=M7=Mn-4=(MS-MW)/2(弹塑性)

作用在辊子上的压力可根据各断面力矩平衡条件求得：

P1=2/t×M2=2/t×MS

P2=2/t×[2M2+M3]=6/t×MS

P3=2/t×[M2+2M3+M4]=8/t×MS

P4=2/t×[M3+2M4+M5]=1/t×(7MS+MW)

P5=2/t×[M4+2M5+M6]=1/t×(5MS+3MW)

P6=2/t×[M5+2M6+M7]=4/t×(MS+MW)

P7=2/t×[M6+2M7+M8]=1/t×(3MS+5MW)

P8=2/t×[M7+2M8+M9]=1/t×(MS+7MW)

P9=2/t×[M8+2M9+M10]=8/t×MW

P10=2/t×[M9+2M10]=6/t×MW

P11=2/t×M10=2/t×MW

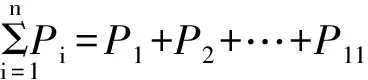
式中，t为辊距。

2 基于曲率积分理论的矫直力计算

2.1 曲率积分理论

所谓曲率积分理论，即用对曲率的变化量进行积分代替对曲率和弯矩进行积分的方法，使得材料的应力应变关系的非线性和辊与板接触的非线性分离[3，4]。基于以上理论，本文将给出矫直过程中应力、应变和矫直力的计算公式。

2.2 钢板和矫直辊接触解析

辊式矫直机的矫直过程比较复杂，为了便于分析和计算，通常假设矫直辊与板材的接触点位于矫直辊的顶点。事实上，板材与矫直辊接触点的位置随着矫直辊的压弯量、板材的原始曲率、板材的厚度以及板材的屈服强度等因素的变化而不同。钢板和矫直辊接触并不是垂直方向的，所以求解钢板与矫直辊的接触点是必要的。矫直辊与板材的接触点位置[6]如图2所示。

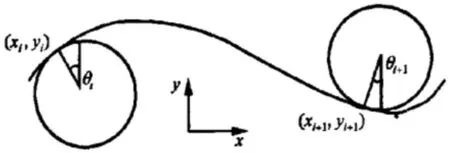
图 2 矫直过程中矫直辊与钢板的几何关系Figure 2 Geometrical relationship between straightener roll and steel plate in straightening process

钢板与矫直辊的接触点(xi，zi)。

计算的收敛条件dzi/dxi=tanθi，即接触点处钢板的斜率和轨迹的接触点处的斜率相等。

可以用如下方程表示[7]：

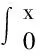
其中，θi为矫直辊垂线与矫直辊接触点(xi，zi)间的倾角，δi为第i辊的压下量。

2.3 应力应变关系

根据弹塑性力学可知，材料在弹性范围内遵守胡克定律，在塑性范围内遵守Prandtle-Reuss增量理论，满足Mises屈服准则。

(1)在弹性范围内

dσx=[E/(1-υ2)]dεx

dσy=[υE/(1-υ2)]dεx

(2)在塑性范围内

dσx={[4H′(1-a+a2)+E(2a-1)2]dεx}/A

dσy={[4H′(1-a+a2)-E(2-a)(2a-1)]dεx}/A

A=(5-4υ)(1+a2)+(10υ-8)a+4H′(1-a+a2)(1-υ2)/E

a=σy/σx

2.4 弯矩和矫直力的计算

单位宽度的弯矩为：

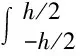
第i辊接触位置全宽度的弯矩为：

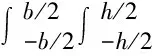
矫直力公式为：

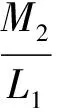
式中，b为宽度，h为厚度，L为辊距。

3 实验研究

采用上述解析方法，基于舞阳新宽厚板厂的全液压可逆十一辊矫直机，实验参数如下：矫直辊数为11，辊径为∅285 mm，辊距为300 mm，辊身长度为4 300 mm，电机型号为AC690V，电机功率为650 kW。上矫直辊5根，下矫直辊6根(包括边辊)。在工作时，上辊系的矫直力由上压力框架传递到压下装置上，而下辊系的矫直力则是通过下辊系传递到机架上。本次实验中矫直力的数据采集是通过液压压下装置测得的。而液压压下装置是采用四个带位移传感器的液压缸实现压下、抬起动作的。

(1)矫直力波形分析

图3给出了矫直力的实测示波图，矫直力的波形具有明显的阶梯性。整个波形由三部分组成，第一部分是矫直过程的建立阶段，矫直力按阶梯状递增；第二部分是矫直过程的稳定阶段，矫直力趋于平稳，表示该辊参与的矫直过程已经形成；第三部分矫直力按阶梯状递减，是矫直过程的解除阶段，最后回零。

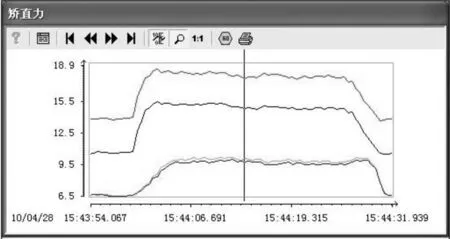
图 3 矫直力实测示波图Figure 3 Oscillogram of actual measurement for straightening force

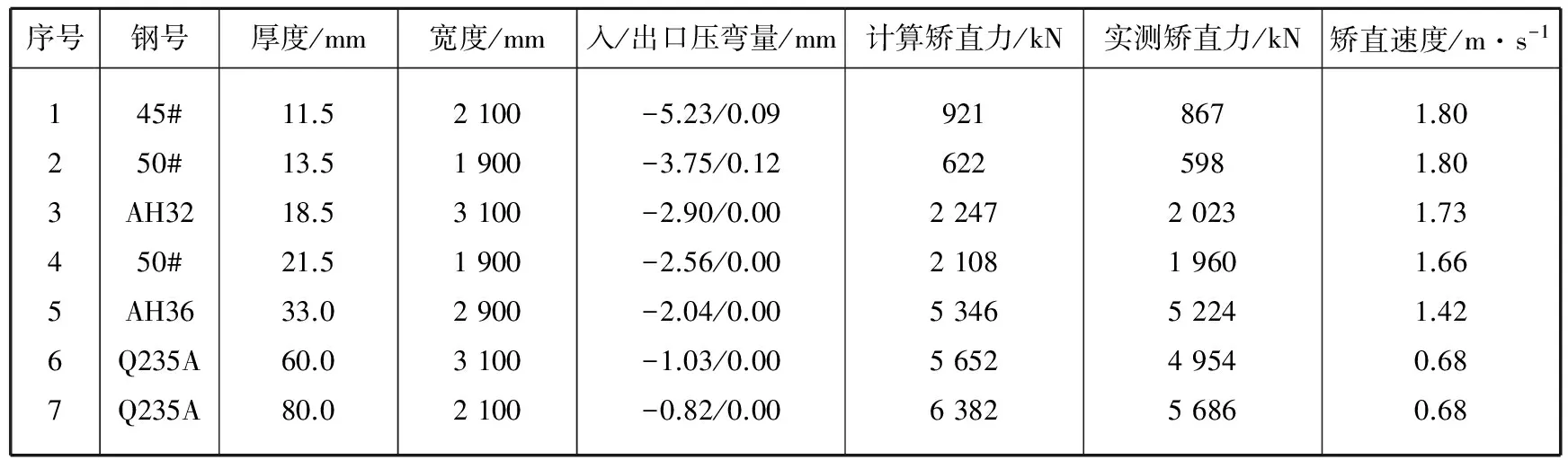
表 1 板材矫直的基本数据

(2)矫直力计算与实验结果比较

采用上述解析方法计算出矫直力的值及实验数据，结果见表1。

4 结论

由表1可以看出，按上述解析方法计算的辊式矫直机的矫直力经试验证明是比较合理的，为矫直机的使用和矫直机参数的确定提供了可靠依据。

[1] 比護剛志，松本纮美，小川茂.ローラ矯正中の被矯正材の曲率に及ぼす応力ひずみ関係の影響[J].塑性と加工，2002，43(496).

[2] 門田浩次， 前田谅一. ローラーしべラーにぉける矯正過程での曲率の解析法[J].塑性と加工，1993，34(388).

[3] 門田浩次，前田谅一.矯正中のロール反力·驅動トルクの解析法[J].塑性と加工，1995，36(409).

[4] 門田浩次，前田谅一.数値解析手法のローラーしべラー設計ヘの応用[J].塑性と加工，1995，36(419).

[5] 崔甫.矫直原理与矫直机械[M]，北京：冶金工业出版社，2002.

[6] 薛军安，胡贤磊，刘相华，王国栋. 辊式矫直过程弹塑性弯曲数学模型[M].钢铁研究学报，2008，11.

[7] Toru Aoyama，Marek Kawka，Shiro Yoshida. Errect of the Compliance of Rolls in the Leveling Process of a Steel Mill.2004 American Institute of Physics.Toru Aoyama，Marek Kawka，Shiro Yoshida. Errect of the Compliance of Rolls in the Leveling Process of a Steel Mill.2004 American Institute of Physics.

Straightening Force Calculation of the Fully Hydraulic 11-roll Straightener

YangXiaojun，WangXiaogang，WangShuhuan

By researching straightening principle, and based on elasticity and plasticity bend theory as well as curvature integral theory, calculating method of straightening force has been obtained.

11-roll straightener；straightening force；calculation

TG333.2+3

A

2010—06—02

杨晓君(1984—)，女，硕士研究生，研究方向：现代轧制设备设计理论与关键技术。

王效岗(1976—)，男，副教授，博士研究生。

王树环(1981—)，女，硕士研究生，研究方向：轧钢工艺及理论。

编辑 杜青泉