论基础货币可控性与货币供应量可控性的关系

黄安仲

(商丘师范学院经济管理系,河南商丘476000)

一、引言

对基础货币与货币量可控性之间关系的研究,通常依据模型M=mB(其中M是货币供应量,B是基础货币,m是货币乘数),并认为:在货币乘数稳定的情况下,如果基础货币是中央银行能够控制的变量,那么货币供应量就具有可控性。反之,如果基础货币不具有可控性的话,即使货币乘数是稳定的,货币供应量也一定不具有可控性。这个结论在研究中得到较为普遍的接受。随着内生货币供给思想的兴起,许多研究货币供应量可控性问题的文献开始把焦点集中到基础货币上,其基本结论是:由于基础货币具有内生性,不是央行能够控制的,因此货币供应量就不具有可控性。在我国经济转型时期,有学者通过证明我国的基础货币不具有可控性,而得出我国的货币供应量也不具有可控性的结论[1](P23)。

在经济转型时期,我国的货币乘数不稳定,而且由于基础货币具有内生性,央行也不能完全控制基础货币[2](P56-59),那么按照目前的研究,货币供应量必然是不可控的。但是目前的研究没有把货币乘数和基础货币对货币供应量可控性的影响联系起来考虑。一旦我们把它们联系起来考虑的话,不可控的基础货币是否必然导致货币供应量不可控呢?

二、文献回顾

对基础货币与货币供应量可控性之间的关系,货币主义者提出货币供应量是基础货币与货币乘数的乘积,即M=mB。并且,货币主义者假设基础货币是中央银行完全可以控制的变量,因此只要货币乘数稳定,中央银行就一定能够控制货币供应量。可见,在货币主义者的研究中根本没有考虑基础货币的可控性问题。随着内生货币供给思想的兴起,人们认识到,即使是基础货币也不是中央银行能够完全控制的,于是产生了基础货币的可控性与货币供应量可控性问题。在假设货币乘数稳定的前提下,Peter在研究货币供应量控制问题时,充分考虑了基础货币变化对货币供应量可控性的影响。他经过研究并得出结论:即使基础货币是变化的,中央银行仍然能够控制货币,因为基础货币各个部分的影响可能相互抵消。Pollin、孙伯银将基础货币视为内生变量,即中央银行不能够控制基础货币,因此也就无法控制货币供应量。Friedman在研究未来的货币政策时提出,由于基础货币逐年减少使得中央银行对货币供应量的控制能力越来越差。Woodford的研究也支持Friedman的这个观点,认为未来电子货币的出现,使得基础货币的需求波动巨大,甚至导致基础货币被电子货币替代,因此中央银行无法通过基础货币来控制货币供应量。McCallum也提出,基础货币一旦受到电子货币的冲击,央行不可能再通过基础货币来实现对货币供应量的控制。Goodhart则提出相反的观点,认为由于基础货币作为支付手段具有独一无二的方便特点,因此它不可能被完全替代,中央银行仍然可以通过基础货币的供给来控制货币供应量。

也有文献将基础货币与货币乘数对货币供应量可控性的影响联系起来考虑。例如托马斯提出,“由美联储操纵的基础货币的变化将会支配货币乘数的变化,从而允许美联储对货币供给进行控制。”[3](P263)山东金融学会的课题组在研究中介目标时,认为:“基础货币与货币乘数是相互作用和相互影响的。”“基础货币增加得多一些,则货币乘数上升就会慢一些;而货币乘数上升得快一些,基础货币增加就会少一些。”[4]

不难看出,关于基础货币的可控性与货币供应量可控性之间关系的研究没有把货币乘数波动可能造成的影响联系起来考虑。货币供应量的可控性是由基础货币和货币乘数这两个变量同时决定的,因此这种孤立的研究方法是否恰当是值得商榷的。尽管有学者也提出了货币乘数和基础货币的变化是相互影响的,但是他们只是提出了一个观点,没有进行深入分析并提供有说服力的证据。鉴于此,本文试图将货币乘数和基础货币对货币供应量可控性的影响联系起来,研究我国经济转型时期基础货币与货币供应量可控性之间的关系。

三、理论模型及基本命题

我们仍依据货币乘数模型来研究基础货币的变化与货币供应量可控性之间的关系。我们的研究考虑了货币乘数随机变化的影响。为此,我们假设货币乘数是不稳定的。进一步,我们把货币乘数分为长期稳定的变化趋势m0和一个短期随机冲击μm,则货币乘数m=m0+μm。同时我们假设,基础货币也不是由中央银行完全控制的,且基础货币的变化可以分为长期稳定的变化趋势B0和一个随机扰动ζB,则基础货币B=B0+ζB。我们假设,无论是货币乘数还是基础货币,它们长期稳定的变化趋势是可以预知的,而随机变化则是不可预知的。在同时考虑货币乘数不稳定和中央银行不能够完全控制基础货币的情况下,货币供给就是:

方程(1)右边的第一项就是在货币乘数稳定,以及中央银行可以完全控制基础货币供给的情况下,中央银行调节基础货币所引起的货币供应量的变化,这项是已知的。后面三项则是在考虑了货币乘数不稳定以及基础货币存在随机的内生冲击情况下它们对货币供应量的冲击。从方程(1)我们可以看出,货币乘数不稳定确实使货币供应量的可控性受到了冲击,但是由此就断定货币乘数不稳定必然导致货币供应量不具有可控性则是不正确的。中央银行能否通过基础货币调控货币供应量,关键是看(m0ζB+μmB0+μmζB)具有怎样的性质。将方程(1)两边同除以m0B0,则得到:

不难看出,我们可以用δ来表示中央银行对货币供应量的控制程度。如果δ接近1,则表明中央银行对货币供应量具有较好的控制力,反之,如果δ偏离1,则表明中央银行对货币供应量的控制力较差,偏离越大,表明中央银行对货币供应量的控制力越差。因此,方程(2)也就是中央银行对货币供应量控制能力的函数。对方程(2)化简并整理得到:令则得到δ=1+α+β+α β。从上面的理论模型中,我们可以得出:

命题:在中央银行不能够完全控制基础货币,以及货币乘数不稳定的情况下,中央银行控制货币供应量的能力取决于两个条件:一是中央银行不能够控制的基础货币随机冲击和中央银行控制的基础货币变化的比值,与货币乘数随机冲击与其长期值的比值的大小接近;二是这两个比值的作用方向相反,这两个条件之间的关系是并集的关系。

当基础货币内生冲击变化和中央银行控制的基础货币变化的比值较小时,则α β趋于零。同时,若α β＜0,那么α+β就可能等于零,于是δ=1依然可能成立。

总之,中央银行对货币供应量的控制能力取决于货币乘数波动、基础货币波动的大小及方向。简单地依据基础货币不具有可控性而得出货币供应量不具有可控性的结论是不恰当的。虽然中央银行不能够完全控制基础货币,但是货币乘数的随机波动可能会抵消基础货币不可控所带来的影响。因此,要判断我国经济转型时期中央银行是否能够控制货币供应量,必须研究我国货币乘数波动、基础货币波动的大小及其相互关系。

四、中国经济转型时期货币乘数波动性研究

(一)货币乘数的随机波动

如果一个时间序列变量是稳定的,则它必须满足:(1)期望值与时间无关;(2)方差值是有限的,且不随时间而变化。如果一个时间序列是不稳定的,则其均值和方差将随时间而改变。依据这种研究方法,我们计算并判断我国经济转型时期的货币乘数是否具有稳定性。由于中央银行的负债必然等于其资产,因此,基础货币供应量必然等于中央银行的资产量,所以我们用中央银行的负债代替基础货币B。货币供应量分别用狭义货币供应量M1和广义货币量M2表示,狭义货币乘数m1=M1/B;广义货币乘数m2=M2/B。为了直观起见,我们将广义和狭义货币乘数的季度均值和方差显示在图中(为节省篇幅,图形省略),时间区间为2000年第1季度到2009年第四季度,数据来源于中国人民银行网站。从图中我们可知,狭义货币乘数各个季度的均值大约为1.35,其方差几乎为零,而广义货币乘数的方差季度之间波动较大。据此,我们得出结论:广义货币乘数是不稳定的,而狭义货币乘数则是相对稳定的。

(二)货币乘数的随机波动幅度

本文选择ARIMA计量模型研究货币乘数的预测性。这个模型的基本理论是假设狭义货币乘数m1和广义货币乘数m2从长期来看能够回归到均衡状态,而误差项存在序列相关性,因此m1和m2就表现为在某一长期均衡值附近上下波动,且其误差不断调整的过程。m1和m2可以根据均值、方差和离散系数这三个指标做出判断。经计算,得出这三项指标值显示在表1中。从表1中可以看出,狭义货币乘数m1比广义货币乘数m2的波动性更小。以上分析表明,对m1和m2分别建立单纯的ARIMA模型在理论上是成立的。根据上文货币乘数的定义m=m0+μm,μm就是货币乘数的预测误差。误差计算公式如下:

表1 m1和m2的代表性指标统计

为了清楚地看出预测的准确性,我们用预测误差除以实际值作为预测误差率。通过计算,我们可以发现,在样本期间,我国货币乘数预测偏差很不稳定,其中有的季度预测性很好,可达到0.286%,而有的年份甚至偏差接近8%,其平均偏差接近4.43%,即β=μm/m0=4.43%。

五、基础货币的波动性研究

(一)基础货币冲击与货币乘数随机变化的关系

为了便于分析,我们特定义:流通中的现金C=M0;活期存款D=M1-M0;储蓄存款是S;准货币Z=M2-M1;定期存款T=Z-S;基础货币B=C+R(R为存款准备金)[5](P133)。因此,现金比率k=C/D;法定准备金率r=R/(D+T+S);超额准备金率re=Re/(D+T+S);定期存款率t=T/D;储蓄存款率s=S/D,故而狭义货币乘数和广义货币乘数分别为:

方程(7)清楚地告诉我们,狭义货币乘数与法定准备金率、超额准备金率、定期存款率以及储蓄存款率成反向关系,但是与现金比率之间的关系并不明确。为了弄清现金比率与狭义货币乘数之间的关系,我们对(7)求k的导数,得:

由于 t∈(0,1),s∈(0,1),则 1+t+s＜3。因此从方程(9)我们可以得出:如果 r+re＜1/3,则dm1/dk＜0,即狭义货币乘数和现金比率的变化就是反向关系。实际上,如果按照正常的储蓄存款率和定期存款率计算的话,要使得狭义货币乘数与现金比率保持正向关系的话,法定准备金率和超额准备金率之和需要达到50%以上,在银行商业化不断深化的今天,这样高的准备金率是难以想象的,所以我们可以认定狭义货币乘数和现金比率之间是负向关系。同理,我们可以得出:

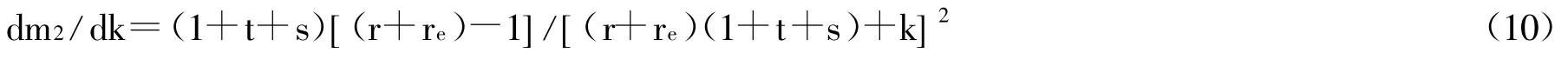
由于r+re＜1,所以广义货币乘数与现金比率之间存在明确的负向关系。

如果家庭的现金比率、定期存款率、储蓄存款率均达到合意水平,而银行在既定的法定准备金率下,超额准备金率也到达理想水平,此时,如果中央银行通过公开市场操作,便产生了一次性的基础货币供给增加。中央银行公开市场操作导致的结果可能包括:一是商业银行完全吸收了基础货币供给的变化,即C=0,此时家庭依然处在原来的状态上,不会做出任何反应,如果基础货币的增加量完全被商业银行以超额准备金的形式持有的话,则超额准备金率必然上升,即货币乘数必然下降。二是家庭完全吸收了基础货币供给的变化,即R=0,此时家庭的现金比率必然上升,按照上面的分析,这也必然导致货币乘数的下降。三是基础货币被商业银行和家庭两个部门持有,则结果还是货币乘数下降。类似地,我们可以得出货币乘数与上述各个影响因素之间都是负向关系。

综上分析,基础货币的变化与货币乘数之间存在反向关系。既然基础货币冲击和货币乘数变化是反向的,那么中央银行通过公开市场操作增加基础货币将导致货币乘数在短期内下降。

(二)B0与ζB的关系

基础货币的供给取决于中央银行的资产规模。我国中央银行目前吞吐基础货币的主要渠道包括再贷款、再贴现、外汇买卖以及财政在中央银行的净借款余额的变化。中央银行一次性的基础货币供给的变化,必然改变经济运行的环境,进而改变中央银行的资产规模,由此会产生基础货币的内生供给冲击。如果说中央银行对再贷款、再贴现等尚具有控制能力的话,那么外汇则是中央银行不能控制的,因此外汇变化将产生中央银行不能够控制的基础货币供给冲击。按照弗里德曼的货币理论,中央银行一次性的基础货币调整,对利率将会产生三个效应:初期的冲击效应、中期的收入效应和价格水平效应以及长期的价格预期效应。

第一,初期的冲击效应。弗里德曼认为,央行增加货币的短期效应是由流动效应和第一轮可贷资金效应组成的。流动效应在利率和名义货币量之间,或者相当于在它们之间产生一种关系。如果中央银行增加基础货币,“就我们目前狭义的理论框架而言,除了公众持有超额现金之外最初不会发生什么。……毕竟,这种增加是不可预期的,并且现金被当作一种存量的吸收器而持有。”[5](P46)由于超额现金的积累,现金持有者会发现他们的资产结构已经失调,因此试图调整资产结构。在这个过程中,他们会哄抬商品以及其他资产价格,并迫使利率下降。这便是“纯粹的流动效应”。

第二,中期收入效应和价格水平效应。随着时间的推移,初期的冲击效应会被中期的收入和价格水平效应所取代。即使不能被预期到,中央银行增加基础货币而导致的货币供应量增加和最初的利率下降会刺激支出,进而影响价格和产出,而这又会影响货币需求。这些变化倾向于提高利率,抵消来自流动效应和第一轮可贷资金效应对利率产生的下降压力。另外,“或迟或早这种名义收入的加速将不得不采取提高价格的方式,因为假设的最初状态是一种均衡状态,且并没有采取什么措施去改变实际收入的长期趋势。”[6](P127)“不过,无论名义收入的加速是否采取产出或者价格加速的形式,利率的数量效应都是相同的”,即“趋于提高利率”[5](P48)。因此,按照弗里德曼的理论,中央银行增加基础货币在中期必将导致利率水平的上升。

第三,长期的价格预期效应。即使最初的货币增加没有被预期到,但最终也会被公众知道,随着价格和利率的上升,公众的预期将是迫使利率进一步上升的压力,从而使得“名义利率一定会高于最初水平”[5](P590)。在资本流动的情况下,中央银行增加基础货币,在短期内由于利率是下降的,将可能阻止国际资本的流入。但短期之内,由于汇率贬值必然导致出口增加,从而导致经常项目顺差,增加外汇收入。如果经常项目的外汇收入增加大于资本项目外汇收入的减少,则短期之内外汇收入将是增加的。但在中期和长期,利率的提高必然导致国际资本的流入,从而引起资本项目的顺差。

可见,基础货币冲击和中央银行能够控制的基础货币的变化方向既可能是一致的,也可能是不一致的。在中国经济转型时期,中央银行可以控制的基础货币与基础货币的随机冲击之间的具体关系,只能借助实证研究来发现。

(三)B0与ζB、ζB与μm的关系以及ζB/B0的实证检验

由于基础货币量是由中央银行资产规模决定的,因此我们用中央银行的资产总额表示基础货币B。那么从t期到t+1期的基础货币变化率就是λt=(Bt+1-Bt)/Bt。经计算,我们得出E[λ]=0.045。因此,由方程λt=(Bt+1-Bt)/Bt,我们可以得到基础货币的预测公式就是Bt+1=1.045Bt+ζBt。我们将Bt+1=1.045Bt称为基础货币中能够被中央银行准确预知的部分,用B0表示,而误差项ζB t表示基础货币中不能够被中央银行预知的部分。我们将不可预知的基础货币变化视为基础货币的随机冲击。

我们将各个季度中能够被中央银行准确预知的基础货币和不能够预知的基础货币的统计结果列示在表2中。从中我们可以清楚地看到,除了个别季度外,不可预知的基础货币只占可预知的基础货币的4%左右,其平均预测误差为 3.98%,也就是说,ζB/B0=α≈3.98%。

我们进一步检验中央银行可观测的基础货币的变化与中央银行不可观测的基础货币之间的关系。我们用本季度的B0值与其上个季度值之间的差代表中央银行可以观测的基础货币的季度间变化。不可观测的基础货币ζB通过实际值与预测值之间的差计算得到,并将中央银行可以观测的基础货币的季度变化和不可观测的基础货币ζB之间的关系绘成图(为节省篇幅,该图省略)。从该图中我们可以清楚地看出,中央银行可以控制的基础货币和中央银行不能控制的基础货币随机冲击之间存在明显的正向关系。因此我们可以得出结论:如果中央银行增加基础货币,那么经济自身也将通过特定的渠道增加基础货币供给;反之,如果中央银行减少基础货币供给,那么经济自身也将减少基础货币供给。

我们将基础货币的随机波动ζB和广义货币乘数的短期波动μm联系起来,绘成图以考察它们之间的关系(为节省篇幅,该图省略)。从该图中可以清楚地看到,在我国经济转型时期,基础货币的随机波动和广义货币乘数的短期波动之间存在反向关系。

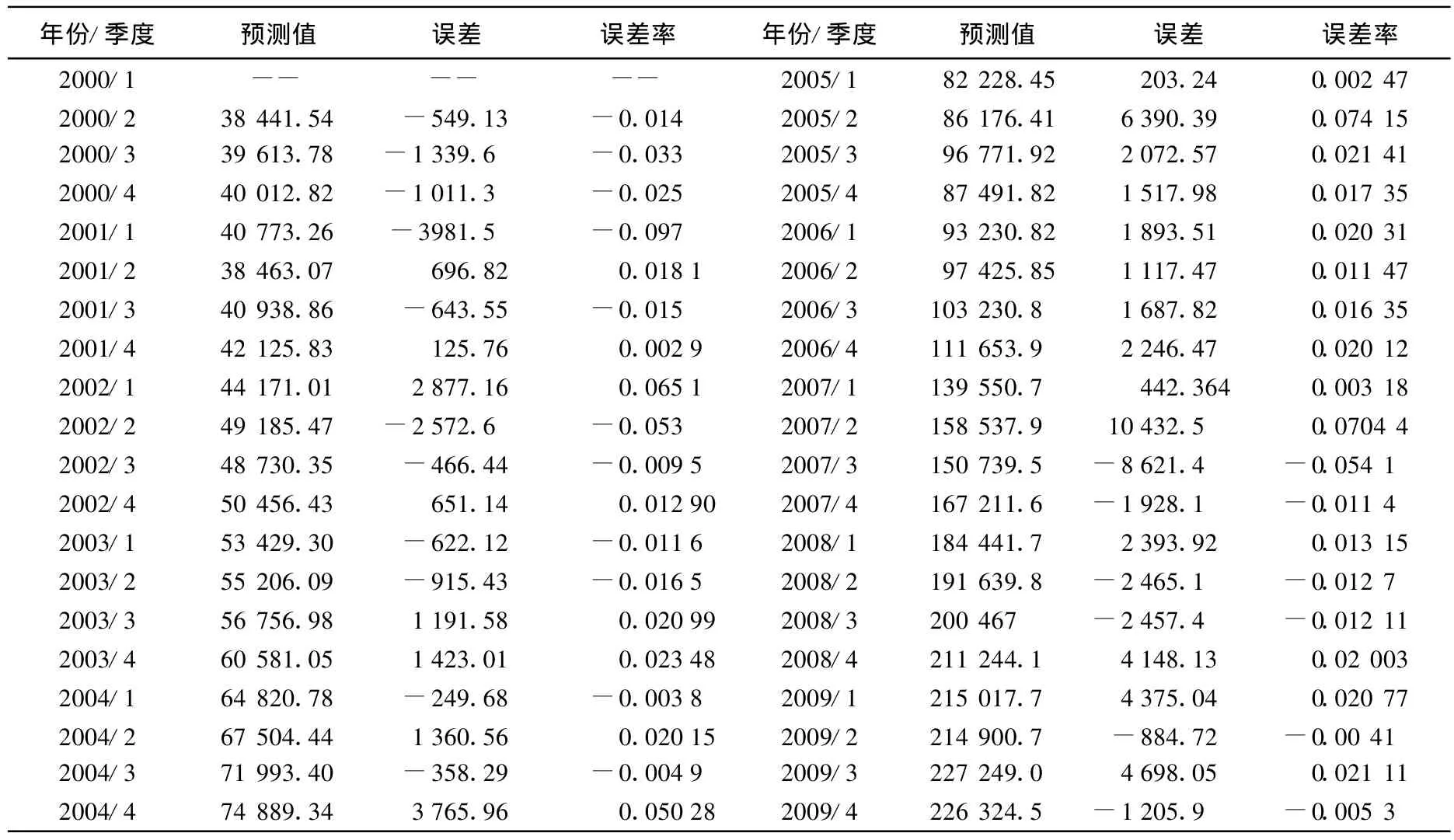
表2 基础货币可预测和不可预测部分的统计值

六、结论

理论分析表明,在中央银行不能够完全控制基础货币的条件下,货币供应量是否具有可控性就取决于货币乘数和基础货币波动的幅度,以及它们之间的相互关系。在特定的情况下,基础货币的冲击可能会抵消由于货币乘数对货币供应量带来的影响,从而提高中央银行对货币供应量的控制能力。这个特定的情况取决于中央银行不能控制的基础货币随机冲击在中央银行能够控制的基础货币中所占的比率,以及货币乘数随机冲击与其长期稳定值的比率,只要这两个比值的作用方向相反,且数值大体相等,那么货币供应量依然是可控的。

实证分析表明,在我国经济转型时期,狭义货币乘数相对稳定,而广义货币乘数既不稳定,且其短期随机波动占长期稳定值的比率约为4.43%。研究还表明,在我国经济转型时期,尚有3.98%的基础货币是中央银行不能够控制的,从而形成基础货币的随机冲击。中央银行能够控制的基础货币与基础货币的随机冲击之间是正向关系,而与货币乘数之间是反向关系。因此,基础货币的随机冲击和货币乘数的随机冲击对货币供应量的影响部分地相互抵消了,从而提高了中央银行对货币供应量的控制能力。

[1]胡海鸥,马晔华.货币理论与货币政策[M].上海:上海人民出版社,2004.

[2]许健.中国经济转轨中的货币控制[M].北京:中国金融出版社,1997.

[3]劳埃德·B·托马斯.货币、银行、与金融市场[M].北京:机械工业出版社,1999.

[4]山东金融学会“我国货币政策中介目标、工具及传导研究”课题组.从货币供给的内生性谈我国货币政策中介目标的选择[J].济南金融,2002,(6):3-6.

[5]弗里德曼,施瓦茨.美国和英国的货币趋势[M].北京:中国金融出版社,1991.

[6]方兴起.货币学派[M].武汉:武汉大学出版社,1999.