定基指数的趋势测定与应用

胡国强,马鹏程

(河南财经学院 统计学系,河南 郑州 450002)

在实际工作中计算某经济社会现象的平均发展速度一般用几何平均法，计算平均发展速度的方程式法平时很少用.无论用哪一种方法计算的平均速度,都是反映该经济社会现象在某一段历史时期的环比速度的一般水平[1].在统计学教科书中，都不讨论定基发展速度的平均数计算问题.

如果借助于平均发展速度进行预测，理论上讲，应该用几何平均法计算，因为几何平均法计算平均发展速度的基本原理是基于事物最末期水平.但是，几何平均法的平均发展速度极易受最初或最末期水平的影响.那么，用这样的平均发展速度进行预测的结果也就有理由受到怀疑.

问题是，能不能根据所研究对象的发展速度的历史资料直接测定出定基发展速度的趋势值，用来进行预测，这样既避免了几何平均法的平均发展速度受极端数值的影响，又为预测带来了灵活方便；不但测定出定基速度的趋势值，还可得出环比速度的平均数.本文就此进行了讨论.

1 定基速度趋势值的测定方法

由于事物的定基发展速度等于环比展速度的连乘积，所以事物各期的定基发展速度一般呈现出明显的几何级数增长型.由此得到启发，我们为定基发展速度配合指数曲线以模拟其趋势，指数曲线的一般形式为：

(1)

把(1)式两边取对数，得：

(2)

(2)式称为(1)式的对数直线式.用普通最小二乘法容易求出lnα0和ln(1+r).若用手工计算，则：

(3)

(4)

(5)

2 应用举例

中国1998至2008年GDP及各年可比价发展速度[2,3]如表1所示.

表1 我国历年GDP的发展速度及其预测值Tab.1 The speed of development of China’s GDP over the years and its predicted value

2.1 计算平均速度

以时间序号t为自变量、以定基速度Rt为因变量,用最小二乘法拟合的对数直线方程(本文用Eviews软件计算)为：

(-4.26) (54.58)

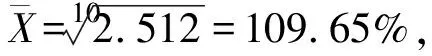
(6)

用(6)式计算的各年以1998年为固定基期的定基速度趋势值见表1末栏.

2.2 进行预测

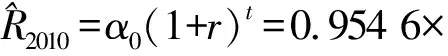
上述预测过程是以1998年的实际水平为基数进行预测的.而某个具体年份的实际水平很可能受偶然性不规则因素影响，这也是导致预测值不准确的一个原因.为了改善预测结果，应该在预测值中充分体现近期数值提供的信息.因此，应该以离预测期最近的若干年GDP实际水平的平均值为基数进行预测.仍以预测中国2010年GDP为例，应用2006至2008年GDP实际值的平均数254 041.13亿元为预测基数，该基数应视为2007年的趋势值，即以2007年为基期进行预测.此时，(6)式中2007年的t=0， 2010年的t=3.所以，2010年以2007年为基期的发展速度预测值为127.23%.则以2007年价格计算的2010年我国GDP预测值为:

323 216.53(亿元).

3 结束语

虽然在理论上有两种计算平均发展速度的方法(水平法和累计法)，但在实际工作中，人们总是常用水平法研究某一事物的平均速度，因为这种方法计算简单，易于理解.而计算平均发展速度的累计法很少有人使用，主要是因为该方法的计算过程较麻烦.从应用条件上讲，水平法适用于某一事物在一定时期内持续上升或下降的状况.如果在一定时期内呈现出大起大落的状况，研究某平均速度则不宜用水平法，适用于累计法.那么，反过来说，累计法是否仅适用于波动性较大的现象呢？我们认为不是.对于持续上升或下降的事物用累计法研究其平均速度同样适合.因此，要把累计法的应用重视起来.无论是水平法和累计法，都是用来研究事物在某一历史时期内的平均速度，即具有“事后算账”的特点.

而要借助于平均速度进行预测未来，我们认为水平法和累计法都不合适.因为水平法平均速度要受极端数值的影响；累计法则考察的不是最末期水平，而是一段时期的累计值.借助于平均速度进行预测应用了本文讨论的“定基指数的趋势测定与应用”方法,该方法既可以用来考察事物未来某特定时期的水平，又充分体现了所有能观察到的历史数据所提供的信息，从而有效地避免了个别极端数值对预测结果的不良影响.

参考文献：

[1] 李冻菊.统计学[M].北京:中国农业出版社，2003. 222.

[2] 国家统计局.中国统计年鉴2008[M].北京:中国统计出版社,2008. 40.

[3] 国家统计局.2008年国民经济和社会发展统计公报[EB/OL].http://www.stats.gov.cn/tjgb/ndtjgb/qgndtjgb/t20090226_402540710.htm.