运用Drucker-Prager准则的深埋圆形硐室弹塑性分析

陈国祥，郭兵兵

(河南工程学院 安全工程系，河南 郑州 451191)

地下硐室是岩石工程建造最多的地下构造物，如公路和铁路的隧道、地下厂房、矿山竖井等.它们有的具有圆形断面的特点，而其他形状的断面也可作近似圆断面来处理.对硐室围岩进行弹塑性区应力、应变分析，将直接指导着地下硐室的施工与设计工作.关于圆形硐室围岩的弹塑性分析一直广泛引用修正的Fenner 方程，它基于的屈服条件为库仑-莫尔准则[1,2].库仑-莫尔屈服准则并没有考虑中间主应力对屈服特性的影响，而研究表明，中间主应力对岩石屈服还是有一定的影响作用的[3-5].但由于传统因素，工程界一直沿袭至今.Drucker-Prager准则计入了中间主应力的影响，又考虑静水压力的作用，克服了基于库仑-莫尔准则的不足.因此，本文将以Drucker-Prager准则为屈服条件，对深埋圆形硐室围岩作弹塑性分析.

1 塑性区的应力状态

1.1 基本假设

围岩为各向同性、均匀的连续介质，无限长巷道处于原岩应力为p0的均匀应力场中，侧压系数λ=1，巷道断面为圆形，属轴对称问题，可作平面应变处理.符合深埋条件，埋深大于或等于20倍巷道半径,其模型见图1.

图1 圆形硐室围岩弹塑性分析模型Fig.1 Elastic and plastic analysis model of circular roadway for surrounding rocks

1.2 塑性区应力

将Drucker-Prager准则作为岩石进入塑性状态的判据，该起塑条件[2，6]为：

(1)

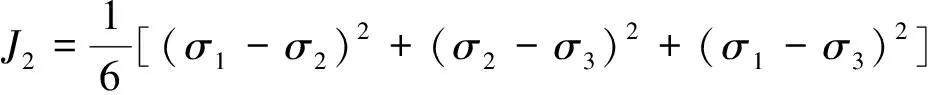
当λ=1时，可认为切向应力σθ为最大主应力，径向应力σr为最小主应力，而轴向应力σz为中间主应力，则I1、J2改写成：

I1=σii=σθ+σr+σz

(2)

(3)

轴对称问题的平衡方程为：

(4)

这儿塑性区的应力符号(σθp、σrp)在脚标上加以区分.

设硐室围岩塑性区体积应变εm为0[1,2]，对平面应变εz=0和塑性区体积应变εm=0的情况，轴向应力σzp与σθp、σrp的关系[7]为：

(5)

将式(5)、(3)、(2)代入式(1)得：

(6)

代入式(4)得：

(7)

解此微分方程并利用边界条件：r=rα、σrp=pα可得，

(8)

(9)

1.3 塑性区半径

通常将弹塑性分界点称作为塑性区半径.根据条件：r=Rp，σθp=σθe；σrp=σre.利用式(8)、式(9)和当λ=1时，弹性应力应满足的条件：σre+σθe=2p0，建立如下公式：

(10)

(11)

由上式看出，塑性区半径与巷道半径、原岩应力、围岩内摩擦角φ、粘结力c以及支护阻力有关.上式还表明，围岩具有自承能力，对于一给定的pa，硐室围岩会通过调整塑性圈半径来维持自身的平衡.支护阻力越大，塑性区半径越小.对于不同埋深的硐室，在围岩性质变化不大的情况下，深部巷道要想获得与浅部巷道相同或相近的稳定性，就必须施加更大的支护阻力.

2 弹性区的应力状态

围岩弹性区的应力可直接引用平面应变轴对称的结果：

(12)

(13)

式中，σR0为塑性区边界处的径向应力.

由式(8)得塑性区边界处的径向应力为：

(14)

根据式(12)、(13)、(14)，即可确定弹性区内应力.

对于c=5 MPa，φ=30°，Rp/rα=1.5，pα=0.4 MPa，由式(10)、(14)算得p0=28.2 MPa，σR0=10.5 MPa，用MATLAB可绘出硐室开挖后应力(无标度)重分布曲线如图2所示.

图2 硐室开挖后应力(无标度)重分布曲线Fig.2 Dimensionless stresses redistribution curves

3 与修正的Fenner 方程比较

松动圈理论[8，9]认为，松动圈半径，即塑性区半径是硐室进行支护设计的主要依据之一.因此，有必要对修正的Fenner 方程和本文推导得的塑性区半径作一比较.修正的Fenner 方程确定的塑性区半径为：

(15)

式(11)与式(15)比较，可知其影响因素均为巷道半径、原岩应力、围岩内摩擦角φ和粘结力c以及支护阻力.两种准则下塑性区半径的变化规律比较如图3和图4所示.

图3 塑性圈半径随内摩擦角φ(Pa=0.4 MPa；P0=15 MPa； C=5 MPa)和原岩应力P0(P0=15 MPa；C=5 MPa；φ=30°)的变化规律Fig.3 Variation of the plastic loosening zone radius R with internal friction angle φ and in-situ rock stress P0

图4 塑性圈半径随粘结力C(Pa=0.4 MPa；P0=15 MPa； φ=30°)和支护阻力Pa(P0=15 MPa；C=5 MPa； φ=30°)的变化规律Fig.4 Variation of the plastic loosening zone radius R with the bonding strength C and the support capacity

由图3和图4可以看出，两者的变化规律具有一致性.而且，在同等条件下，基于Drucker-Prager准则推导出的塑性圈半径要大于修正的Fenner 方程得到的塑性圈半径.这表明，中间主应力对巷道塑性圈半径大小有一定的影响，其影响程度主要与公式(11)和(15)中的四大因素有关.进一步分析发现，内摩擦角在20°～45°内，粘结力较大时，两者的塑性圈半径相差并不大，但粘结力较小时两者相差较大，且相差趋势越来越明显.这说明，如对软岩进行支护设计时，采用基于Drucker-Prager准则推导出的塑性圈半径作为支护设计依据时是偏安全的.

4 结 论

(1)基于Drucker-Prager准则推导出的塑性圈半径随影响因素的变化规律与修正的Fenner 方程变化规律基本一致.而且，由于考虑了中间主应力的影响，在同等影响因素下，前者的塑性圈半径较后者大.围岩内摩擦角在20°～45°以及粘结力较大时，两者的塑性圈半径相差并不大，但粘结力较小时两者相差较大，且相差趋势越来越明显.

(2)由于考虑了中间主应力对岩石屈服的影响作用，克服了修正的Fenner 方程的不足.因此，该推导结果可用于现场巷道支护设计依据.

(3)本文推导基于的准则实际上也是一种理想弹塑性模型，并未考虑到巷道围岩的破坏或应变软化特征.如果考虑到巷道围岩的破坏或应变软化特征，应该可以得到更近实际的圆形巷道周围弹塑性解，这还需进一步研究探讨.

参考文献：

[1] 沈明荣．岩体力学[M]．上海：同济大学出版社，1999．

[2] 蔡美峰．岩石力学与工程[M]．北京：科学出版社，2002．

[3] 高延法．岩石真三轴压力试验与岩体损伤力学[M]．北京：地震出版社，1999．

[4] 许东俊,耿乃光．岩石强度随中间主应力变化规律[J]．固体力学学报,1985,(1):72-80．

[5] 茂木清夫．一般三轴压缩下岩石的流动和破坏[J]．岩石力学,1980,(1):1-14．

[6] 贾乃文．塑性力学[M]．重庆：重庆大学出版社，1992．

[7] KACHANOV L M ．塑性理论基础[M]．北京：人民教育出版社，1982.

[8] 陆士良，汤 雷．锚杆锚固力与锚固技术[M]．北京：煤炭工业出版社，1998．

[9] 侯朝炯．煤巷锚杆支护[M]．徐州：中国矿业大学出版社，1999．