Internet AS层拓扑节点度分布特性的演化规律

邓晓衡, 许华岚, 张连明*

(1. 中南大学信息科学与工程学院, 中国 长沙 410083;2. 湖南师范大学物理与信息科学学院, 中国 长沙 410081)

近年来, 国内外有关Internet拓扑模型和特性的大量研究表明, 不同层次的Internet拓扑具有相同、相近或不同的特性[1]. 例如, Internet AS (Autonomous System)层, 路由器层和应用层的WWW拓扑的节点度均具有幂律分布特性和小世界效应[2]; AS层拓扑和WWW拓扑均显示匹配特性[3], 而很少有关于路由器层拓扑是否具有匹配特性的相关报道; AS层拓扑呈现富人俱乐部特性[4], WWW拓扑具有自相似特性[5], 而路由器层拓扑是否存在富人俱乐部特性或自相似特性, 以及AS层拓扑是否存在自相似特性和WWW是否具有富人俱乐部特性等有待进一步研究[6]. 为深入揭示潜在的AS层拓扑特性, 理解实际AS层拓扑的演化规律与趋势. 本文基于节点度阈值重整化算法研究Internet AS层拓扑的节点度分布特性及其演化规律.

1 Internet AS层拓扑节点度分布特性及其演化规律分析方法

1.1 节点度分布特性

在Internet AS层拓扑图中, 1个AS代表拓扑网络的一个节点, 2个ASes之间的互联关系代表拓扑网络的一条链路. 研究表明, Internet AS层拓扑的节点度k与节点度概率密度函数p(k)满足幂律关系[7], 即

p(k)∝k-γ，

(1)

其中,γ称为幂指数, 式(1)称为节点度幂律分布函数. 一般情况下, 满足幂律分布特性的实际网络幂指数的取值范围为: 2<γ<3.

节点度幂律分布是Internet AS层拓扑的一个重要特征, 它表现为网络中存在大量的低度节点(拥有少量连接的节点)和少量的高度节点(拥有大量连接的节点), 幂指数是这一类节点度分布规律的一个量化指标. 在实际应用中, 为了更好地体现网络拓扑的节点度幂律分布特性, 一般使用补累积度分布函数P(k)来替代概率密度分布函数p(k).P(k)与节点度k和幂指数γ存在如下关系:

P(k)∝k-γ+1.

(2)

显然, 公式(2)可以由公式(1)两边对k积分得到.

1.2 演化规律分析方法

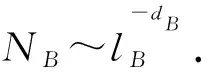
上述研究结果同时也表明, 这些复杂网络在重整化前后的度分布p(k′)具有不变特性, 即

p(k)→p(k′)∝(k′)-γ.

(3)

最近, 文献[9]对复杂网络重整化前后的自相似特性和无标度节点度分布的不变特性进行深入研究, 指出式(3)缺乏严格的数学证明和大量的数据验证, 进而推导出如下公式:

(4)

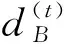
从公式(4)可知, 当Ct>1和t约等于网络的平均距离时,C0…Ct-1为网络平均距离的指数函数, 这也暗示网络规模为平均距离的一个指数函数, 此时网络不具有自相似特性. 不过到目前为止, 这一结果还没有得到实际数据的验证.

对于一个复杂网络可能存在多种粗粒度化方法, 在不同粗粒度化过程下获得的复杂网络拓扑特性和演化规律不尽相同[10]. 最近, 文献[11]提出了节点度阈值方法. 与盒覆盖方法相比, 节点度阈值方法不但消除了不同粗粒度带来的影响, 而且更能真实刻画实际复杂网络演化的逆过程.

本文在节点度阈值方法的基础上, 给出一种重整化新算法来分析研究Internet AS层拓扑节点度分布的不变特性和演化规律.

2 节点度阈值重整化算法

节点度阈值方法是指: 给定一个节点度阈值kT, 剔除网络G中节点度小于和等于kT的所有节点, 得到一个全新网络G′. 使用节点度阈值方法针对Internet AS和PGP(Pretty Good Privacy)等复杂网络进行分析[11], 发现网络G和网络G′的节点度分布和节点度-度相关是自相似的, 但聚集系数是非自相似的. 为了探讨Internet AS层拓扑节点度分布特性的演化规律, 本文利用节点度阈值方法来对Internet AS层拓扑进行重整化研究, 给出了一种新的节点度阈值重整化算法. 该算法的基本思想是: 给定一个原始Internet AS层拓扑G和节点度阈值kT(=0,1, …,kmax-1), 一次性剔除拓扑G中节点度小于和等于kT的所有节点以及与这些节点相连接的链路, 剩下的节点与链路所构成的拓扑G′(>kT)称为kT次重整化Internet AS层拓扑, 这里kmax为原始Internet AS层拓扑的最大节点度. 显然, 当kT=0时, 有G′(>kT)=G, 这说明0次重整化Internet AS层拓扑为原始Internet AS层拓扑; 当kT>kmax时, 则有G′(>kT)=Φ, 即kmax次重整化Internet AS层拓扑为空集. 节点度阈值重整化算法的具体实现如下:

(i) 给原始Internet AS层拓扑的每个节点分配一个唯一标号id, 且id=1, …,n, 其中n为网络规模, 同时给出节点度阈值kT.

(ii) 利用一个二维数A[xi,yi]组存储原始Internet AS层拓扑的链路xi→yi, 其中xi和yi分别代表第i条链路的2个节点, 这里1≤i≤m,m为网络的总链路数.

(iii) 对数组进行排序. 先按照第1列xi值对每一行数据进行升序排列; 如果xi值相等, 则按照第2列yj值对每一行数据进行升序排列.

(iv) 排除自环链路(即第1列和第2列相等的那行数据), 也就是删除xi=yi的那些行; 排除平行链路, 即删除满足xi=yi和yi=xi中的其中一条链路. 生成一个新的数组B[xi,yi].

(v) 计算原始Internet AS层拓扑的最大节点度kmax.

(vi) 设置数组行r=1, 另外再设置2个新的空数组, 即C=[]和D=[]. 循环下列步骤, 直到行r等于数组B[]的长度为止.

a) 计算数组B[]的第1列中与B[r,1]相等的元素个数, 记为num1; 计算数组B[]的第2列中与B[r,2]相等的元素个数, 记为num2.

b) 若num1≤kT和num2≤kT, 则把数组元素B[r,:]追加到数组C[]中, 形成重整化Internet AS层拓扑G(>kT).

c)r增加1.

3 实验结果与分析

3.1 数据来源和实验过程

本文采用的Internet AS层拓扑数据来源于文献[12]中的AS1, AS2, AS3和AS4 4组数据.

实验过程如下: 首先对4组数据AS1, AS2, AS3和AS4做简单图预处理, 即去掉自环链路和平行链路, 得到AS1, AS2, AS3和AS4的节点数n分别为12 694, 7 690, 8 689和8 904, 链路数m分别为26 559, 15 413, 17 709和17 653, 最大节点度kmax分别为2 566, 1 713, 1 911和1 921. 然后, 运用第2节给出的节点度阈值重整化算法对AS1, AS2, AS3和AS4数据所对应的Internet AS层拓扑进行重整化, 得到节点度阈值分别为kT=0, 1, 2, …,kmax-1的重整化Internet AS层拓扑.

3.2 Internet AS层拓扑节点度分布特性及其演化规律

为了寻找Internet AS层拓扑的节点度分布特性及其在演化过程中的变化规律或趋势, 我们考查了i(i=0, 1, 2, …,kmax-1)次重整化Internet AS层拓扑节点度分布情况. 图1(a)～(h)显示了数据AS1, AS2, AS3和AS4所对应的Internet AS层拓扑且节点度阈值kT分别取0, 1, 2, 5, 10, 25, 50, 100和200时的重整化Internet AS层拓扑的补累积度分布概率P(k)与节点度k之间的关系(双对数坐标图)(见公式(2)). 从图1(a), 图1(c), 图1(e)和图1(g)可以看出, 当节点度阈值较小(比如kT<10)时, 重整化Internet AS层拓扑节点度具有幂律分布特性(即节点度与补累积度分布概率为近似直线关系). 从图1(b), 图1(d), 图1(f)和图1(h)可以看出, 当节点度阈值较大(比如kT>10)时, 重整化Internet AS层拓扑节点度分布大致可分为2个阶段, 即较小节点度节点满足幂指数较小的幂律分布, 而较大节点度节点满足幂指数较大的幂律分布.

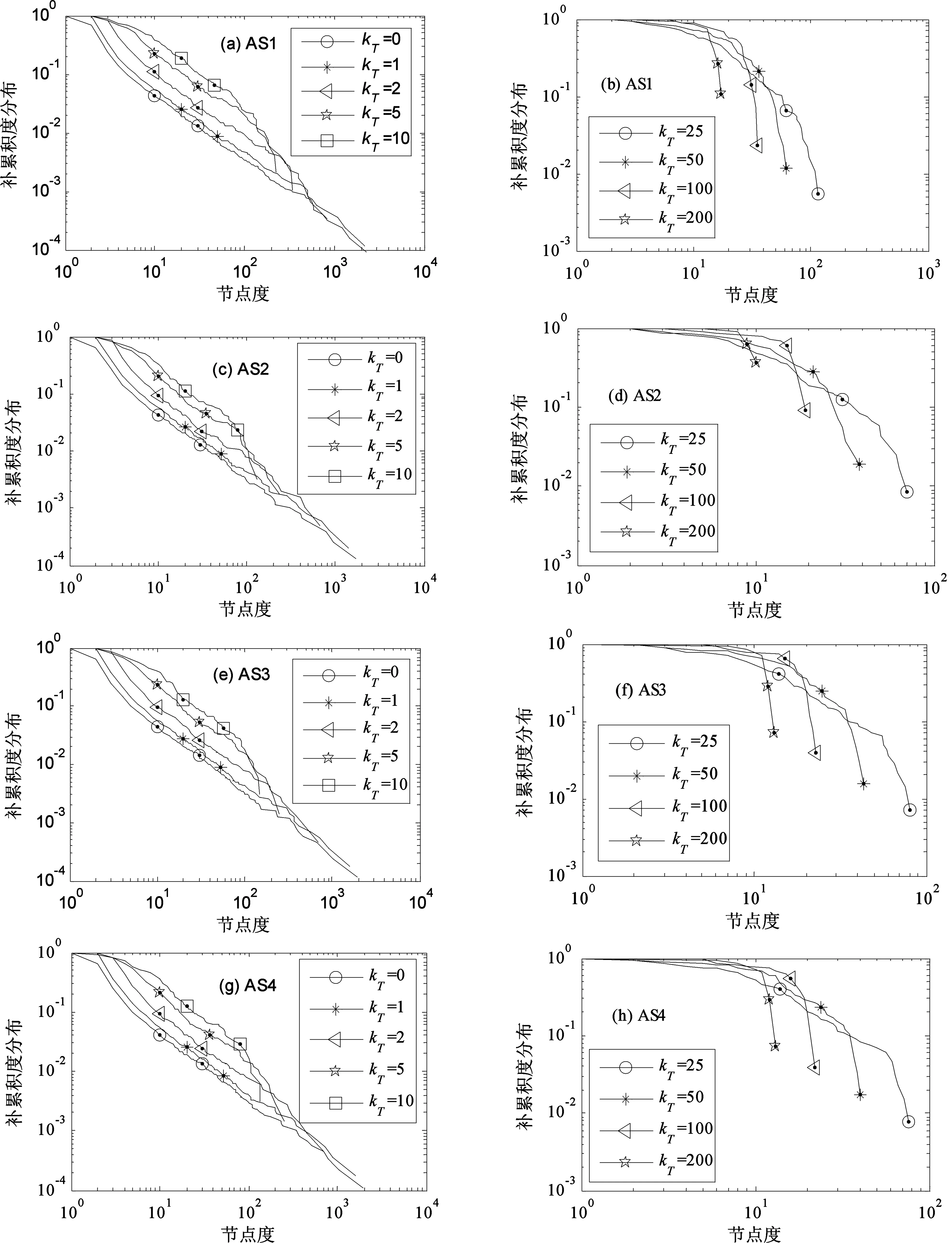
图1 重整化Internet AS层拓扑的补累积度分布

根据节点度分布函数(公式(1))与补累积度分布函数(公式(2))之间的关系, Internet AS层拓扑的幂指数γ的值等于1减去补累积度分布函数曲线的拟合直线的斜率(-γ+1)的值. 通过计算, 我们得到了AS1, AS2, AS3和AS4数据在重整化过程中对应的所有重整化Internet AS层拓扑的幂指数. 表1给出了节点度阈值kT分别取0, 1, 2, 5, 10, 25, 50, 100和200时对应的幂指数γ的值.

表1 重整化Internet AS层拓扑的幂指数值

从表1可知, 当kT=0, 1, 2, 5, 10, 25, 50, 100和200时, AS1, AS2, AS3和AS4数据对应的原始拓扑(kT=0)幂指数值的平均值分别为2.070 9, 2.071 6, 2.061 5, 2.048 8, 2.046 1, 2.047 8, 2.054 1, 2.095 8和2.169 0. 显然, 0次和1次重整化Internet AS层拓扑节点度分布的幂指数基本相等.

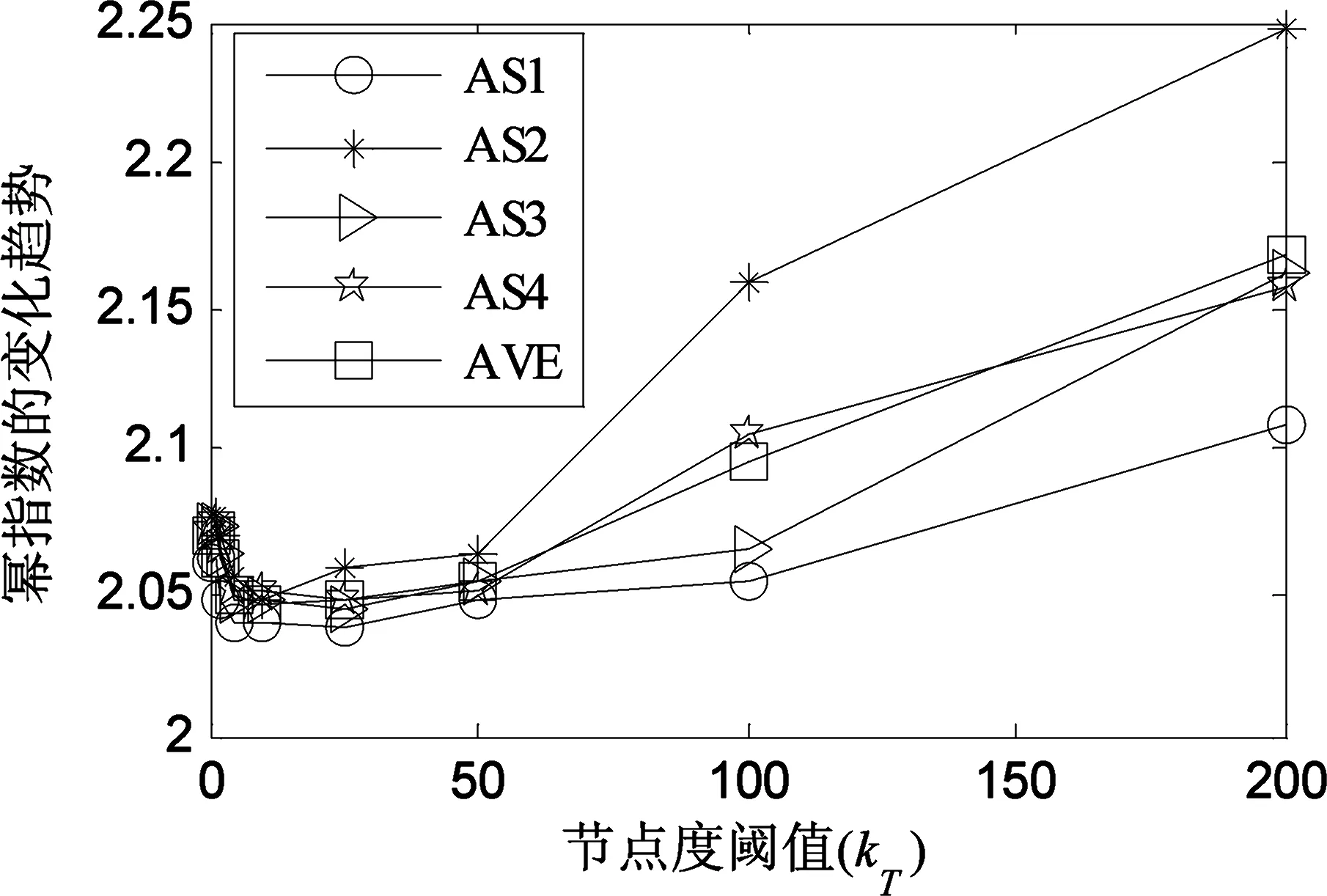
图2 重整化Internet AS层拓扑的节点度幂指数随节点度阈值的变化趋势

图2显示了重整化Internet AS层拓扑的幂指数γ随节点度阈值kT的变化趋势, 其中AVE为AS1, AS2, AS3和AS4数据所对应节点度分布的幂指数的平均值. 从图2可以看出, 当节点度阈值取值范围位于[1,10]区间内, Internet AS层拓扑在重整化前后的幂指数随节点度阈值的增加呈现锐减趋势; 当节点度阈值取值范围位于[10,50]区间内, Internet AS层拓扑在重整化前后的幂指数随节点度阈值的增加而缓慢增加; 当节点度阈值取值范围位于[50,200]区间内, Internet AS层拓扑在重整化前后的幂指数随节点度阈值的增加而快速增加.

综上所述, 我们可以得出如下结论: (1)当今Internet AS层拓扑的节点度分布具有幂律特性, 其幂指数约为2.070 9, 这说明在Internet AS层拓扑中存在大量的低度节点和少许高度节点; (2)在最近一次节点度阈值重整化过程中(即kT=1), Internet AS层拓扑节点度的幂律分布特性基本保持不变, 由拓扑演化是重整化的逆过程可知, Internet AS层拓扑在最近的演化过程中具有节点度幂律分布的不变特性; 随着节点度阈值的增大, 节点度幂律分布的幂指数随节点度阈值的增加而锐减, 这反映Internet AS层拓扑在这个阶段的演化过程中节点度幂律分布的幂指数急剧增加; 当节点度阈值为10到50时, 幂指数随着节点度阈值的增加而缓慢增加, 这说明Internet AS层拓扑在该阶段的演化过程中节点度幂律分布特性具有自相似特性; 当节点度阈值为50到200时, 幂指数随着节点度阈值的增加而快速增加, 这反映了Internet AS层拓扑在该阶段的演化过程中节点度幂律分布特性减弱, 从图1(b), 图1(d), 图1(f)和图1(h)又可以看出, 此时节点度具有两段分布特性, 从总体上看, 该阶段的幂律分布特性增强了; 当节点度阈值接近Internet AS层拓扑节点度的最大值时, 由于拓扑节点总数目较少, Internet AS层拓扑为简单网络而不具有复杂网络特性, 即Internet AS层拓扑节点度分布无幂律特性; 由此可以断定在Internet AS层拓扑的演化发展过程中, 节点度分布的幂律特性的演化规律如下: 首先从无到有, 然后从大幂指数到小幂指数, 最后又从小幂指数到大幂指数; (3)基于节点度阈值重整化算法研究Internet AS层拓扑的节点度分布特性的演化规律是非常有效的.

4 结束语

为了寻找和了解潜在的Internet拓扑的不变特性和动态演化规律, 本文首先归纳分析了基于盒覆盖算法的重整化算法及其不足, 给出了基于节点度阈值的重整化算法, 对Internet AS层拓扑进行重整化, 并在此基础上分析研究重整化Internet AS层拓扑的节点度分布特性及其演化规律. 基于经验数据的研究结果表明, Internet AS层拓扑的节点度分布具有幂律特性且该特性在演化过程中具有不变特性或呈现自相似特性, 发现了Internet AS层拓扑的节点度幂律分布的幂指数大小的动态演化趋势. 上述研究工作和结果不仅有利于理解实际Internet AS层拓扑的不变特性和动态演化规律, 而且可用来对已存在的网络模型进行验证与修正, 并进一步提出更好的新型网络模型.

参考文献：

[1] COLIZZA V, FLAMINI A, SERANO M,etal. Detecting rich-club ordering in complex networks[J]. Nature Physics, 2006, 2:110-115.

[2] ALBERT R, JEONG H, BARABSI A L. Diameter of the world-wide web[J]. Nature, 1999, 401:130-131.

[3] NEWMAN M E J. Assortative mixing in networks[J]. Physical Review Letters, 2002, 89(20):208 701-208 704.

[4] ZHOU S, MONDRAGON R J. The rich-club phenomenon in the internet[J]. IEEE Communications Letters, 2004, 8(3):180-182.

[5] SONG C, HAVLIN S, HERNAN,etal. Self-similarity of complex networks[J]. Nature, 2005, 433:392-395.

[6] KIM J S, GOH K -I, SALVI G,etal. Fractality in complex networks: critical and supercritical skeletons[J]. Physical Review E, 2007, 75: 016 110-016 123.

[7] FALOUTSOS M, FALOUTSOS P, FALOUTSOS C. On Power-law relationship of the internet topology[J]. ACM SIGCOMM Computer Communication Review, 1999, 29(4): 251- 262.

[8] 汪小帆, 李 翔, 陈关荣. 复杂网络理论及其应用[M]. 北京: 清华大学出版社, 2006.

[9] XIAO W J, PENG L M, PARHAMI B. On general laws of complex networks[J]. Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering, 2009, 4:118-124.

[10] ITZKOVITZ S, LEVITT R, KASHTAN N,etal. Coarse-graining and self-dissimilarity of complex networks[J]. Physical Review E, 2005, 71: 016 127-016 136.

[11] SERRANO M A, KRIOUKOV D, BOGUNA M. Self-Similarity of complex networks and hidden metric spaces[J]. Physical Review Letters, 2008, 100:078 701-078 704.

[12] TSAPARAS P. Datasets[M/OL]. http://www.cs.helsinki.fi/u/tsaparas/MACN2006/data-code.html, 2008-8-9.