遗传算法在设施定位问题中的应用研究

马娜，王新生

(湖北大学 资源环境学院，湖北 武汉 430062)

设施定位问题(facility location problem),也称作多韦伯问题(multi-Weber problem)或p-中位问题(p-median problem)[1], 实质上它既包括用户的分配，又包括设施在空间上的定位，所以通常又把设施定位问题称为设施定位一分配问题(facility location-allocation problems).

本文中将设施定位-分配问题分为用户分配、设施定位两个子问题，提出分别采用遗传算法来处理.

1 设施定位问题的数学表达

根据Miller[2]的研究，设施定位问题有两种数学表达形式.

1.1基于平面空间的设施定位问题的目标函数和变量基于连续平面空间的设施定位问题是指在连续平面空间上确定设施的空间位置.给定n个用户对象的集合，设施定位问题的优化目标是确定p个没有限定容量的设施的空间位置，使设施与用户间相互作用费用和设施在选定位置上的固定费用之和最小.其数学表达式如下：

(1)

且满足

(2)

(1)，(2)式中，如果用户i被分配到设施j时，zij=1；否则zij=0.wi是对用户i的需求权重，Ci描述用户i的位置，Fi描述设施j的位置，d(Ci,Fj)表示用户i和设施j间的距离，S(Fi)指设施j选定在某一位置上的费用，n表示用户的数量，p表示设施的个数，(2)式表示每个用户只能接受一个设施的服务.(1)式中待定的变量有两个：分配变量z和隐含在Fj中设施位置的坐标.

1.2基于离散空间的设施定位问题的目标函数和变量基于离散空间的设施定位问题是指在有限个候选设施中选取若干个设施，并为这些设施确定相应用户的问题.假如从m个候选设施中选取p个设施，则问题可表示为：

(3)

(3)式除了要满足(2)式的约束条件外，还应服从下面约束：

zij≤zjj,i,j=1,2,…,n

(4)

(5)

(4)，(5)式中，若候选者j被选择为设施时，zjj=1；否则zjj=0.(4)式表示除非该设施是选定设施，否则不允许将一个用户分配给候选设施.(5)式表示从m个候选设施中选取p个设施.(3)式中要确定的变量是分配变量z.设施的位置坐标隐含在m个候选设施中，不是待定的变量.

设施定位问题中分配子问题是一个一般的指派问题，它是一个已知的NP难问题[1].Miller[2]认为，即使对点状用户、点状设施而言，多设施定位问题都属于求解有多个全局最优解的目标函数问题.如果考虑到设施和用户的空间形状(configuration)，如设施和用户的形状分别为线状或面状，则目标函数更加复杂，因此必须寻求更有效的枚举(enumeration)算法或邻域搜索技术以求得问题的最好解(或近似最优解).

2 遗传算法在设施定位问题中的应用研究

遗传算法GA(genetic algorithm)是模拟自然界生物进化机制的一种算法,即遵循适者生存、优胜劣汰的法则,即寻优过程中有用的保留,无用的去除[3].它将问题域中的可能解看作是群体的一个个体或染色体，并将每一个体编码成符号串形式，模拟生物进化过程，对群体反复进行遗传学的操作(遗传，交叉和变异)，根据预定的目标适应度函数对每个个体进行评价.依据“适者生存”进化规则，不断得到更优的群体.同时以全局并行搜索方式来搜索优化群体中的最优个体，求得满足要求的最优解[4].

由于遗传算法的通用性、隐含并行性和稳健性(robustness),该算法日益引起各方面的广泛关注，在实践中有许多成功的例子[5-7].

设施定位-分配问题可分为用户分配、设施定位两部分.一般来说，离散空间点位的算术平均中心(mean center)在空间上离中位中心(median center)很近(离散点的数量较少或空间分布很离散时，偏离较多)，中位中心即是指要确定的设施空间位置[8-9]，因此首先将算术平均中心设定为设施位置来确定用户分配子问题，这时问题的目标函数为：

在进行遗传算法的实际应用时，常碰到几个关键问题：由问题空间到遗传空间的编码问题；遗传算子的技术设计问题；遗传算法中各项参数确定和遗传算法过早收敛问题等.

(1)编码和适应度函数

采用类似于Dibble和 Densham的遗传算法编码方法[10]，由p个整数组成的染色体码串表示设施中用户分配状况，如码串为111122223332的染色体，表示有12个用户、3个设施的定位问题的一个可能解，序号为1，2，3，4的用户分配到编号为1的设施，序号为5，6，7，8，12的用户分配到2号设施，序号为9，10，11的用户分配到3号设施.这种编码方式可以保证染色体长度最短，有效地减少当变量过多，码串过长时，二进制编码出现的“海明悬崖”(hamming cliffs)问题[11].

针对本具体问题，用平均中心来代替设施空间位置来进行遗传算法的计算，如上述编码中是先确定序号为1，2，3，4的用户的算术平均中心，计算该平均中心与这4个用户的距离和，其余的依次类推，适应度函数即是这些距离的总和.由随机法产生的初始群体是由p个整数组成的，所以变异操作是将当前的某个整数以相等的概率随机地转换为其它(p-1)个整数中的任意一个整数.另外，在计算个体适应度之前，还须对二进制码串进行译码(decode)，本研究中不是直接将其转换成十进制数，而是转换成各平均中心与其相应用户间距离之和.

(2)遗传算子的设计

在此应用中，选择机制采用联赛选择方法(tournament selection model)，即从群体中任意选取一定数目的个体(称为联赛规模)，本例联赛规模选取为2，其中适应度最高的个体保存到下一代.这一过程反复执行，直到保存到下一代的个体数达到预先设定的数目为止.

杂交方法采用一致杂交算子(uniform crossover)，即通过设定屏蔽字(mask)来决定新个体的基因继承两个旧个体中哪个个体的对应基因.

变异技术采用基本变异算子，即变异仅以一定的概率(通常很小)对串的某些位作值的变异[6].

(3)实验结果

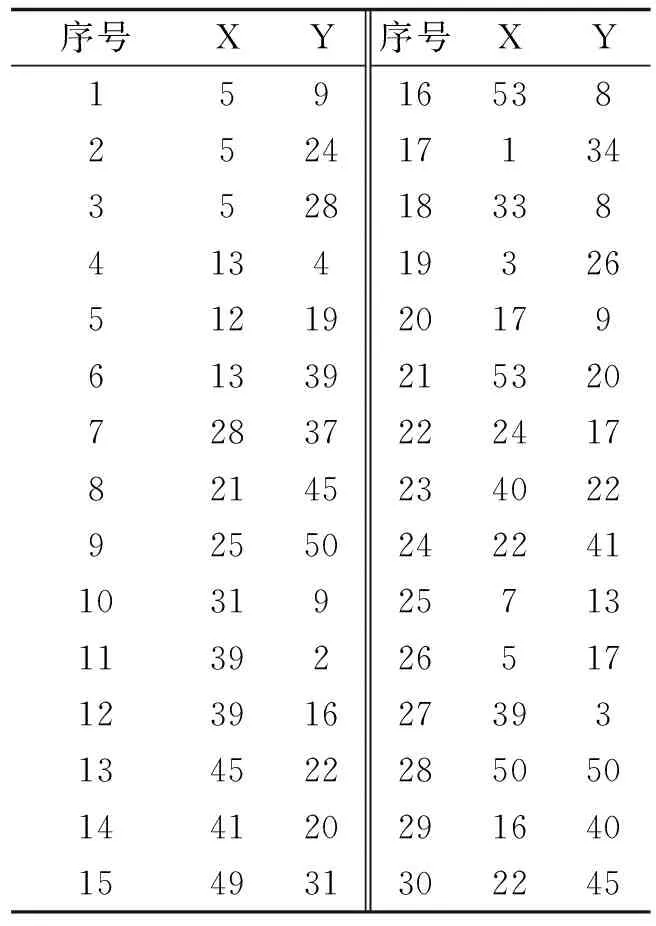
表1 Cooper 和Rosing的实例的用户坐标

我们按照上述设计编制了相应的程序，并进行计算测试.实验中，我们对遗传算法中各项参数进行了反复测试，最后选定群体规模为100，杂交概率为0.65，变异概率为0.005，初始可行解群体由随机法产生，设定若干代内(如100代)适应度函数无变化时运行终止.由于本实验的问题规模很小，最好结果都在200代内达到.实验中仅考虑设施在连续平面空间上定位的情况，不考虑设施在平面上不同地点的固定投资.

用Cooper和Rosing的例子来测试本方法的有效性.这些例子为测试我们提出的方法的有效性提供了一个好的标准，因为Rosing已经计算出它们的全局最优解[1](表3).这些实例包括30个用户，其位置坐标见表1.用户需求看作是相同的，并假设设施没有能力约束[1].当采用各用户子集的算术平均中心为中位中心或设施空间位置时，计算得出的用户分配结果见表2.

表3中的误差百分比计算如为：(实际计算值-最优值)/最优值×100%.当p=3时，我们计算的目标函数值为306.399 7，这比Rosing方法计算的全局最优解307.372还要低，认为我们的结果是正确的，我们得到的3个设施的坐标分别为(6.889 7,16.598 5)、(21.359 3,44.304 2)、(39.086 1,15.993 5).或许Rosing方法的计算结果有精度误差.从表2、表3可以看出，如果将算术平均中心作为设施位置(即中位中心)，计算的目标函数值就已十分接近问题的最优解，这也说明算术平均中心在空间上与中位中心很近.当用户分配子问题确定以后，多设施定位问题变为单设施定位问题，再经过遗传算法求解，计算结果较Cooper的ALA方法效果好，与已知的全局最优解误差不大.这说明了本研究中所采取的解决问题方法的有效性.

另外，需要说明的是，我们也对本方法进行了较大规模的设施定位问题(用户达到数百个，设施十余个)的试验，从遗传算法的设计上完全可以处理这种规模的问题，但是即使我们对基本遗传算法(simple genetic algorithms)作一些改进，如采用自适应杂交、变异[12]、遗传-灾变算法[13]和重新起动[14]等策略，在有限的时间内还是不能收敛到全局最优解，我们正在进一步寻求其它的改进方法.

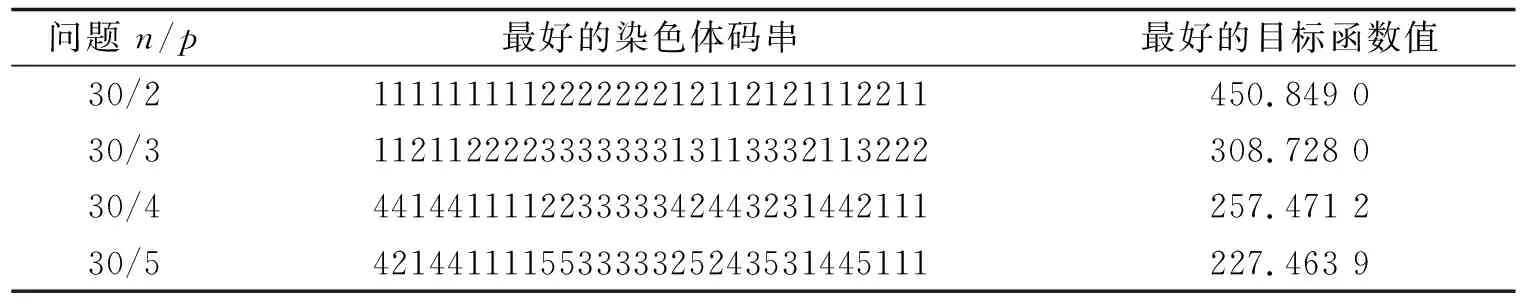
表2 基于遗传算法的用户分配结果

表3 与Cooper 和 Rosing实例的结果比较

3 结语

由于遗传算法的主要特点是群体搜索策略和群体中个体之间的信息交换，操作是根据优胜劣汰的原则，算法在收敛性、全局优化方面都较传统搜索方法优越.正如前面所述，设施定位问题是一个NP难问题，对解决此类遗传问题算法是有效的.

参考文献：

[1] Gen M,Cheng R. Genetic algorithms and engineering design[M].New York:John Wiley and Sons,Inc,1997.

[2] Miller H J. GIS and geometric representation in facility location problems[J]. International Journal of Geographical Information Systems,1996,10(7):791-816.

[3] 李华昌,谢淑兰,易忠胜.遗传算法的原理与应用[J].矿业,2005,14(1):87-90.

[4] 乔均俭,付丽君,徐雅玲.应用遗传算法原理确定函数的最优解[J].微计算机信息,2007,23(6):240-241.

[5] 王春水,肖学柱,陈汉明.遗传算法的应用举例[J].计算机仿真.2005,22(6):155-157.

[6] Rubenstein-Montano B,Zandi I. Application of a genetic algorithm to policy planning:the case of solid waste[J].Environment and Planning B:Planning and Design,1999,26(6):893-907.

[7] richard J B,John T T,Michael R B, et al. Multiobjective urban planning usinggenetic algorithm[J]. Journal of Urban and Development,1999,125(2):86-99.

[8] 郭仁忠.空间分析[M].武汉:武汉测绘科技大学出版社,1997:191-201.

[9] Robert G C.Digital cartography[M].Prentice Hall:New Jersey,1991:165-176.

[10] Dibble C,Densham P J.Generating interesting alternatives in GIS and SDSS using genetic algorithms[M].In Proceeding of GIS/LIS’93(Bethesda:American Society of Photogrammetry and Remote Sensing and American Congress on Surveying and Mapping),1993:180-189.

[11] Zbigniew M.Genetic algorithms + data structures=evolution programs[M].Berlin Heidelberg:springer-Verlag,1996.

[12] 徐勇.一种基于自适应遗传算法的聚类分析方法[J].系统工程与电子技术.1997,19(9):39-43.

[13] 孟祥萍,张化光,何巍.一种基于二进制编码的改进遗传算法[J].吉林工业大学:自然科学学报,1999,29(3):79-83.

[14] 孟祥萍,张化光.一种快速综合性的遗传算法[J].东北师大学报:自然科学版,1998,4:13-17.