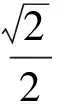用代换法求无理函数的值域

● (常福一区90幢302室 江苏常熟 215500)

用代换法求无理函数的值域

●周华生(常福一区90幢302室 江苏常熟 215500)

用代换法求无理函数的值域，方法简便、灵活，是一种很有用的解题方法.本文就4种常见的无理函数求值域问题从整体上分析一些解法和技巧，可供参考.为计算方便，本文使用以下3个公式(也可用判别式求):

1 求y=+(a>0,c<0)的值域

当a,c同号时，用增减性解很方便.

y的最小值可视具体情况通过所在的点来计算.

2 求y=-(a>0,c>0)的值域

当a,c异号时，可用增减性很方便地求解.

(1)

或

(2)

图1

图2

②当c

即

②当c>a时,k0>1，如图4.可按切线确定截距最小值,于是

即

图3

图4

3 求y=-x(a>0,x≥0)的值域

或

流动资金暂按年运行费的10%计。流动资金从项目正常运行期的第1年初投入，随项目运行，计算期末一次回收［3］。

(4)

(1)当a>1,b>0时，如图5，k0<1.由双曲线方程(3)，且切线确定截距最大值,得

即

图5

图6

即

即

图7

图8

(4)当01，得双曲线方程(4)，如图8，可按切线确定截距最小值为

从而

即

4 求y=kx+t+的值域

为避免复杂的讨论，下面用实例来说明解题的方法.

解原方程可化为

其定义域由-2x2+13x-18≥0确定，即

即

即

解得

图9

图10

图11

时，截距-s取最小值，此时

即

最后指出，本文前3个部分介绍的是一般的解题方法.对于具体问题，可按照所提方法直接求解，这比代公式方便许多.