一个图形的演变与推广

● (杭州外国语学校 浙江杭州 310024)

一个图形的演变与推广

●吴锋刃(杭州外国语学校 浙江杭州 310024)

几何图形变幻莫测，一个个精美的结论更是赏心悦目，几何思维独特且具有丰富内涵，分析综合法、定性推导和定量计算使我们感受证法的曲折离奇；一题多解，各种证法层出不穷、千姿百态；类比联想、加深推广，让人体会到硕果累累，美不胜收.本文将从欣赏数学的视角，从一个学生熟悉的图形开始入手，探讨一些几何题之间的纵横联系，由表及里加深认识、推广，以期能锻炼大家的几何思维、感受几何的独特魅力.

1 图形的基点梳理

如图1，PA，PB切圆于点A，B，OP交AB于点M，PEF为割线，延长EM交圆于点G，很容易获得以下熟悉的结论：

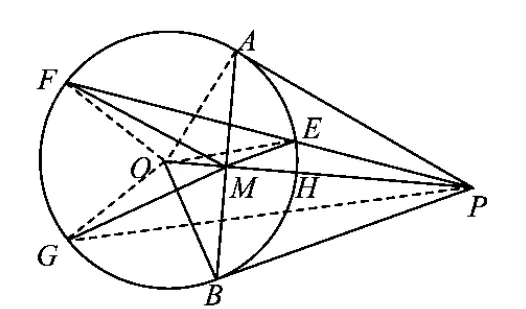
图1

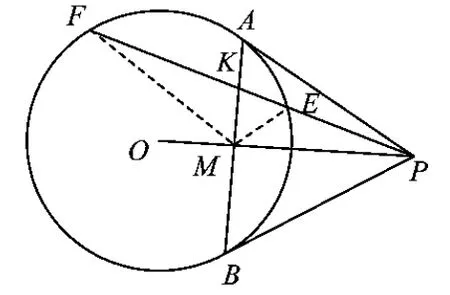
图2

结论1O，G，P，E四点共圆，O，M，E，F四点共圆.

由OM·MP=AM2=ME·MG和PE·PF=PA2=PM·PO可得.

结论2PM平分∠EPG，MA平分∠EMF.

由点O,G,P,E共圆,得

∠EPM=∠OGM=∠OEM=∠GPM.

由点O,M,E,F共圆,得

∠EMP=∠OFE=∠OEF=∠OMF.

结论3MP与圆的交点H是△PEG的内心.

结论4圆上任意一点E满足EM∶EP=AM∶AP(Apollonius circle).

由结论3可得EH平分∠MEP,从而

故动点E在M,P确定的Apollonius circle上面.

2 图形的纵向思考

(2002年全国初中数学联赛试题)

分析由结论2可知，MK平分∠FME.又OP⊥AB，可得MP为∠FME的外角平分线，从而

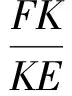
于是

亦称点P，K调和分割线段EF.

当且仅当a=b时等号成立.

思考2如图3，过圆外一点P向圆作2条切线，切点为A，B，过点P作割线PEF，PCD，FC和ED交AB于点M,过PM作割线PST,求证：

(1997年中国数学竞赛试题)

图3

图4

例1如图4,H为锐角三角形PBC的垂心，由点P向以BC为直径的圆作切线，切点为E，F,求证:点E，H，F共线.

(1996年中国数学竞赛试题)

显然,这是思考2问题中的一个特殊情形.

图5

图6

思考3如图5，P是△ABC内一点，D,E分别是△APB和△APC的内心，且AP,BD,CE相交于一点，证明:∠APB-∠ACB=∠APC-∠ABC.

(第37届IMO试题改编)

∠PAB+∠PCB=∠PAC+∠PBC,

即

∠PBC-∠PCB=∠PAB-∠PAC.

而由结论1和结论2,可知∠PCB=∠OPB,即

∠PBC-∠PCB=∠POB=2∠PAK.

由结论4可知AK平分∠BAC,从而

∠PAB-∠PAC=2∠PAK，

故结论成立.

思考4如图7，E，F，G，H是圆O上的4个点，FE，HG交于点P，FH，EG交于点Q，过点P作圆O的2条切线，切点为R，S，则点Q，S，M，R共线.

而由塞瓦定理和梅氏定理可得

因此P,K调和分割线段EF(注意这一结论的证明与圆O无关.对于一般四边形，只要FE,HG交于点P，FH,EG交于点Q即可)，点K在SR上.同理可证点K′也在SR上，从而点Q,S,M,R共线.

进一步很容易发现，点O为△PMQ的垂心(证明略).

图7

图8

3 图形的推广尝试

尝试1图7中除点P，K调和分割线段EF外，还有点Q，M调和分割线段SR(思考2已证明)，Q，M调和分割线段KK′，且E,F,G,H这4点共圆这一条件也并非必须.即：如图8,有以下结论：G,M调和分割线段BA(这一结论图7中已经给出)，F,E调和分割线段MN，或表述为

而

尝试2如图9，E，F，G，H是圆O上的4个点，FE，HG交于点P，过点P作圆O的割线分别交圆O于点L，M，分别交对角线EH，FG于点S，T，交EG，FH于点Q，C，则

图9

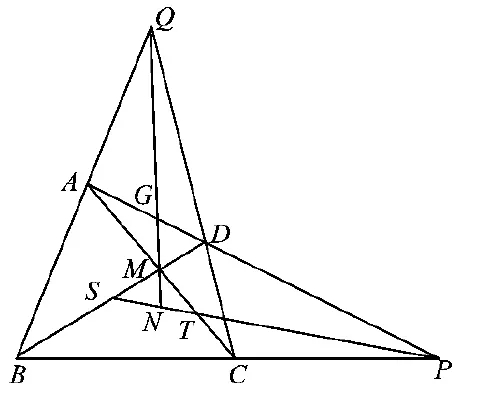
图10

因此

以上3个结论的等式若采用解析法证明,则更为简便，可将与圆的交点、与四边形对角线的交点、与四边形的两边的交点归结为同一问题.证明如下:

x2+y2-1+λ(y-k1x+k1a)(y-k2x+k2a)=0.

它既可表示对角线所在的曲线方程,又可表示边所在的曲线方程.设割线PLM的方程为y=k(x-a)，联立后得

即

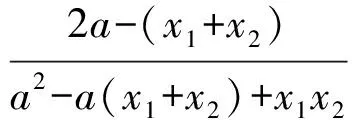
亦即

-a2(x1+x2)+2ax1x2=-2a+x1+x2,

代入x1+x2和x1x2验证即得所证命题成立.