向量空间中若干问题的入微分析和研究

刘学鹏

(临沂师范学院,山东临沂 276005)

向量空间中若干问题的入微分析和研究

刘学鹏

(临沂师范学院,山东临沂 276005)

对向量空间中若干有代表性的问题进行了深入细致的分析和研究.

过渡矩阵;坐标;基础解系;线性相关;线性无关

大凡高等代数或线性代数读者,对向量空间理论的抽象性很可能仍记忆忧新,尤其对正在学习这部分内容的在校大学生,也肯定已经体会到向量空间的理论难以理解.基于此,我们的确有必要对向量空间中有代表性的问题进行深入细致的分析及研究.本文所论及的问题对正在学习或复习这部分内容的读者可能会有所裨益,这也正是笔者所期待的.

另外,本文为线性代数理论系列研究的继续,因为文[4],[5]及[6]已就线性代数理论中的逆向问题、反例问题和命题的正误推论做了较为详尽的分析和探讨.

问题1 求过渡矩阵的技巧性问题.

点评 (i)求过渡矩阵的方法,通常可以采用定义法,即将“后”基的各向量用“前”基表示出之后,再以坐标为列构作的矩阵即是所求的过渡矩阵,尽管此法“少慢差费”,但这却是好的基础;

(ii)在上述推导过程中,我们已经得到了P=B-1A,这时,只要求出B-1,然后再与A相乘,同样可以得到所求的过渡矩阵.

读者不难发现,求过渡矩阵的方法还是以构作新矩阵,然后进行初等行变换的方法简捷,因为这样确能够收到事半功倍之效.

问题2 齐次线性方程组与基础解系的关系.

我们知道,齐次线性方程组永远是有解的.且当其系数矩阵的秩小于未知量的个数时,必有基础解系.现在来讨论已知基础解系时,如何求齐次方程组.

注 已知齐次线性方程组的基础解系,反求原齐次线性方程组的方法,读者可参见文献[1] (P290-292).不过,我们这里用下面的方法.

例2 设某齐次线性方程组的基础解系为

试求这个齐次线性方程组.

解 设所求齐次线性方程组的系数矩阵为A.由题设知,秩A=5-2=3.则所求方程组只有三个独立方程,两个自由未知量,且所求方程组的一般解为

问题3 向量的坐标与线性方程组的增广矩阵的关系.

设向量β在基α1,α2,…,αm下的坐标为(x1,x2,…,xm),则

点评 求向量的坐标,我们上面的推导是利用了线性方程组的理论,将文献[1](P442-444)的方法1和方法2进行了有机的结合,从而使得依据充分,方法简捷而明快.

问题4 向量的线性相关性与齐次线性方程组的解之间的关系.

判断向量组α1,…,αm的线性相关性一般借助关系式

由此可得到向量的线性相关性与齐次方程的解的水乳交融的关系.即

向量组α1,…,αm线性相关(无关)⇔齐次线性方程组AX=0有非(只有)零解⇔秩A＜=m.

点评 这是一个较为普通的问题,但应引起读者重视的是,问题普通但却非常重要,因向量的线性相关性是向量空间理论乃至整个高等代数或线性代数理论的重要基础.

关于这类问题的例子,各家高等代数或线性代数教科书及相关资料均有所列举,故而我们不再举例.

问题5 向量的线性组合(表示)与线性方程组解的关系.

今设向量α1,…,αm,β均为列向量,若β是α1,…,αm的线性组合,即有一组数x1,…,xm,使得

这是由线性组合到线性方程组的微妙微肖的转化.故而可见:

β是α1,…,αm的线性组合⇔线性方程组AX=β有解⇔秩

问题6 向量α,β的线性相关性与二阶行列式的关系.

我们知道,在欧氏空间V中有著名的柯西—布涅可夫斯不等式,即对∀α,β∈V,有

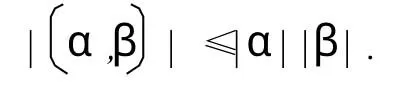
今联系二阶行列式给出等号的证明.

点评 这是何等的巧妙!因为只要利用向量α,β作出上面的二阶行列式,问题就迎刃而解了,所以,技巧就是构作二阶行列式,而构作的二阶行列式主要是根据要证明的等式的特点.

问题7 柯西—布涅可夫斯不等式的巧妙应用.

点评 这个证明也是相当美妙!美妙在利用所给的两个正实数m,n作出了两个向量α与β,随即利用了内积的通常定义.

问题8 欧氏空间中向量夹角定义的自然性.

在中学数学中有余弦定理:设α,β为三角形的任意两边(向量表示),则另一边为β-α,若α,β的夹角为θ,则有

这正是欧氏空间中向量夹角的定义.

点评 (i)对于抽象问题的定义能够借助已有的知识自然给出,这对于读者(尤其是初学者)的记忆和理解应该说是很有帮助的;

[1] 毛纲源.线性代数解题方法技巧归纳(第二版)[M].武汉：华中理工大学出版社,2003.

[2] 周士藩,等.高等代数解题分析[M].南京：江苏科技出版社,1985.

[3] 王卿文.高等代数学综论[M].香港：香港天马图书有限公司,2000.

[4] 刘学鹏.线性代数理论中几个问题的逆向研究[J].大学数学,2005,21(5)：112-115.

[5] 刘学鹏.线性代数理论中经典命题的反例研究[J].大学数学,2007,23(6)：174-177.

[6] 刘学鹏,徐传胜.线性代数理论中两个典型命题的正误推论研究[J].高等数学研究,2008,11(6)：16-18.

An In-depth Analysis and Research of Some Issues in Vector Space

L IU X ue-peng
(Linyi Normal University,Linyi,Shandong,276005,China)

To make an in-depth and detailed analysis and study on several representative issues in vector space.

transistion matix;coordinate;basic set of solutions;linearly dependent;linearly independent

O151

C

1672-1454(2010)03-0173-04

2007-08-24;[修改日期]2008-03-28