N维“格子笼”图的Hamilton问题
2010-11-22唐干武
唐干武, 王 敏
(1.桂林师范高等专科学校数学与计算机科学系,广西桂林 541001; 2.烟台大学数学与信息科学系,山东烟台 264005)
N维“格子笼”图的Hamilton问题
唐干武1, 王 敏2
(1.桂林师范高等专科学校数学与计算机科学系,广西桂林 541001; 2.烟台大学数学与信息科学系,山东烟台 264005)
对n维“格子笼”图的Hamilton性进行了研究,得到了判定n维“格子笼”图是Hamilton图的一个非常简洁的充分必要条件.
n维“格子笼”图;Hamilton圈;计算机基色;色阶
1 基本概念
在计算机色彩设置中,红、绿、蓝是色彩设置中的三种基色,它们可分有0~255个一共256色阶,我们可以用一个三维向量(R,G,B),(R,G,B为整数且0≤R,G,B≤255)来描述一种颜色.人们提出一个有趣的问题:能否从(0,0,0)开始,把所有颜色一一显示出来,要求任意相邻两种颜色的色阶之差为1,并最终回到(0,0,0).即若记Ci=(Ri,Gi,Bi),(Ri,Gi,Bi取0~255间的整数),要确定一个序列
C0(0,0,0),C1(R1,G1,B1),C2(R2,G2,B2),…,C2553(R2553,G2553,B2553),C0(0,0,0),
使得对序列中的任意相邻两个元素Ci(Ri,Gi,Bi)与Cj(Rj,Gj,Bj),有
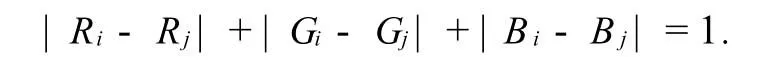
这样的问题可以归结为:对于一个这样的图G,其顶点集为向量(x,y,z)的集合,其中x,y,z分别是0到255之间的整数.当表示两顶点的向量(xi,yi,zi),(xj,yj,zj)的差的模为1时,这两顶点相邻接(即存在边),这样的图是否存在Hamilton圈的问题.文[1]将这样的图称为“格子笼”图,并在文中证明了这样的图存在Hamilton圈.文[2]讨论了当x,y,z取值的上界各不相同时所构成的“格子笼”图的Hamilton圈存在性问题.本文将三维“格子笼”图推广到n维“格子笼”图(n≥2),并得到n维“格子笼”图存在Hamilton圈的充分必要条件.
设ri(i=1,2,…,n,n≥2)是大于或等于1的整数,对无向图G,其顶点集为
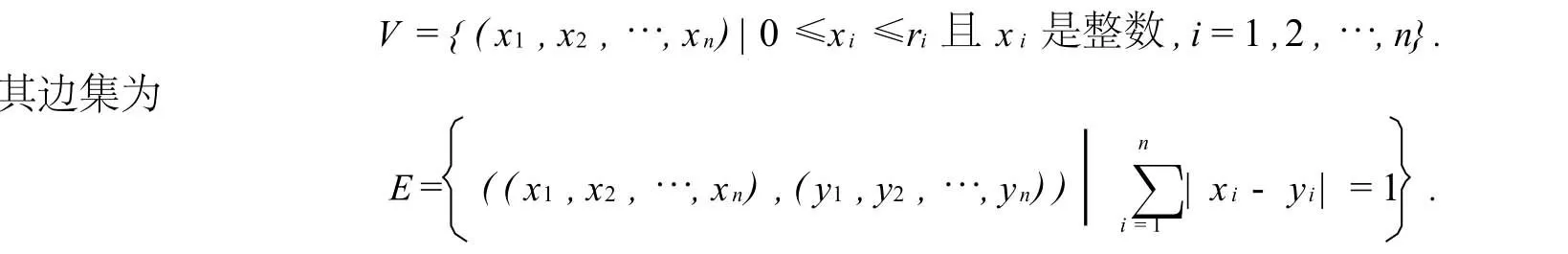
对于给定的ri(i=1,2,…,n,n≥2),图G=(V,E)称为n维“格子笼”图.这样的n维“格子笼”图是否存在Hamilton圈,是一个有趣的问题.下面我们来具体讨论.
2 主要结果及证明
定理2.1 n维“格子笼”图G存在Hamilton圈的充要条件是ri(i=1,2,…,n,n≥2)中至少有一个为奇数.
定理的必要性证明要用到下面两个引理.
引理2.1[3]一个简单无向图为偶图的充要条件是不含奇圈.
引理2.2[3]若G=(V,E)是一个Hamilton图,则对于顶点集V的每一个非空子集S,均有
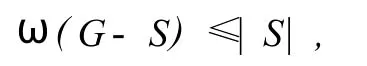
这里ω(G-S)表示子图(G-S)的连通分支数.
定理的证明 充分性的证明.若ri(i=1,2,…,n,n≥2)中至少有一个为奇数时,不妨设r3是奇数,此时只需在n维“格子笼”图G中找出一个Hamilton圈即可.现将G的顶点列成表1.

表1 图G的顶点

(0,0,0,r4,0,…,0)(1,0,0,r4,0,…,0),(2,0,0,r4,0,…,0),…,(r1,0,0,r4,0,…,0)…………(0,0,0,r4,r5,…,rn)(1,0,0,r4,r5,…,rn),(2,0,0,r4,r5,…,rn),…,(r1,0,0,r4,r5,…,rn) (0,1,0,r4,r5,…,rn)(1,1,0,r4,r5,…,rn),(2,1,0,r4,r5,…,rn),…,(r1,1,0,r4,r5,…,rn)…………(0,r2-1,0,r4,r5,…,rn)(1,r2-1,0,r4,r5,…,rn),(2,r2-1,0,r4,r5,…,rn),…,(r1,r2-1,0,r4,r5,…,rn) (0,r2,0,r4,r5,…,rn)(1,r2,0,r4,r5,…,rn),(2,r2,0,r4,r5,…,rn),…,(r1,r2,0,r4,r5,…,rn) (0,r2,1,r4,r5,…,rn)(1,r2,1,r4,r5,…,rn),(2,r2,1,r4,r5,…,rn),…,(r1,r2,1,r4,r5,…,rn) (0,r2-1,1,r4,r5,…,rn)(1,r2-1,1,r4,r5,…,rn),(2,r2-1,1,r4,r5,…,rn),…,(r1,r2-1,1,r4,r5,…,rn)…………(0,1,1,r4,r5,…,rn)(1,1,1,r4,r5,…,rn),(2,1,1,r4,r5,…,rn),…,(r1,1,1,r4,r5,…,rn) (0,0,1,r4,r5,…,rn)(1,0,1,r4,r5,…,rn),(2,0,1,r4,r5,…,rn),…,(r1,0,1,r4,r5,…,rn)…………(0,r2,r3,r4,r5,…,rn)(1,r2,r3,r4,r5,…,rn),(2,r2,r3,r4,r5,…,rn),…,(r1,r2,r3,r4,r5,…,rn) (0,r2-1,r3,r4,r5,…,rn)(1,r2-1,r3,r4,r5,…,rn),(2,r2-1,r3,r4,r5,…,rn),…,(r1,r2-1,r3,r4,r5,…,rn)…………(0,1,r3,r4,r5,…,rn)(1,1,r3,r4,r5,…,rn),(2,1,r3,r4,r5,…,rn),…,(r1,1,r3,r4,r5,…,rn) (0,0,r3,r4,r5,…,rn)(1,0,r3,r4,r5,…,rn),(2,0,r3,r4,r5,…,rn),…,(r1,0,r3,r4,r5,…,rn)
显然,表1中任意相邻的两个顶点在图G中也是相邻的.因为r3是奇数,所以表1排列的顶点共有偶数行,于是易找出G的Hamilton圈.例如,如图1示意的连接方式就构成G中的一个Hamilton圈.
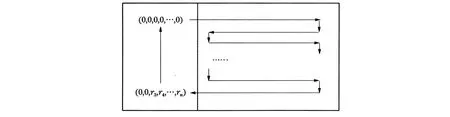
图1 Hamilton圈示意图
必要性的证明.若所有ri(i=1,2,…,n)为偶数,则n维“格子笼”图G的顶点数(r1+1)(r2+1)…(rn+1)为奇数.又由于n维“格子笼”图G不存在奇圈,所以由引理3.1知G是偶图.设此偶图的二分类为{S1,S2}.因|S1|+|S2|=(r1+1)(r2+1)…(rn+1)为奇数,于是不妨设|S1|>|S2|,由偶图的性质知G-S2=S1是G的独立集,所以ω(G-S2)=|S1|>|S2|.根据引理3.2,n维“格子笼”图G不是Hamilton图,即G不存在Hamilton圈.
推论1 三维“格子笼”图G=(V,E),其中
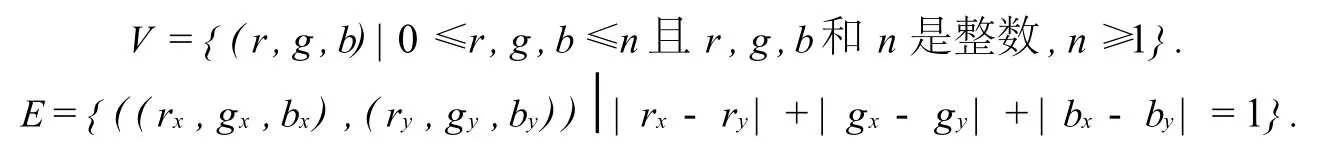
存在Hamilton圈的充要条件是n为奇数.
推论2 三维“格子笼”图G=(V,E),其中
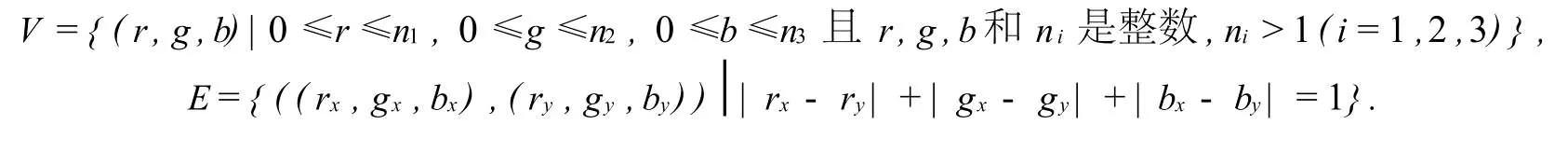
存在Hamilton圈的充要条件是ni(i=1,2,3)中至少有一个为奇数.
[1] 郭常忠,王敏.一种基于RGB三基色的计算机色彩的有序显示算法[J].计算机研究与发展,1997,34(4):312-315.
[2] 李政,王敏.“格子笼”图的Hamilton圈问题[J].大学数学,2007,23(1):147-150.
[3] Bondy J A,Murty U S R.Graph theory with applications[M].New York:MacMillan Press,1976.
[4] 唐干武,王敏.边数q≥C2p-1-1的(p,q)图的泛圈性研究[J].江西师范大学学报,2006,30(6):556-559.
Hamilton Problem onn-Dimensional Cube Graph
TA N G Gan-w u1, WA N G Min2
(1.Department of Mathematics and Computer Science,Guilin Normal College,Guilin 541001,China; 2.Department of Mathematics and Information Science,Yantai University,Yantai 264005,China)
We study the Hamilton properties ofn-dimensional cube graph and give the very simple necessary and sufficient conditions such thatn-dimensional cube graph is a Hamilton graph.
n-dimensional cube graph;Hamilton graph;computer color;levels
O157.6
A
1672-1454(2010)03-0116-04
2007-10-08
广西壮族自治区教育厅科研项目(200807MS032)
