区间数互补判断矩阵的一种新排序算法

史文雷, 徐 蕾

(衡水学院经济与管理学院,河北衡水 053000)

区间数互补判断矩阵的一种新排序算法

史文雷, 徐 蕾

(衡水学院经济与管理学院,河北衡水 053000)

针对区间数互补判断矩阵元素表示的特点,定义了区间数互补判断矩阵的等价矩阵族,得到了区间数互补矩阵一致性检验方法.通过构造一种新的求解区间数互补判断矩阵的权重区间的决策模型,得到一种排序算法.最后给出一个算例,描述此方法的应用.

区间数互补判断矩阵;一致性;排序;模糊互补判断矩阵

1 引 言

由于客观事物的复杂性、不确定性以及人们思维的模糊性和决策信息的不完全性等,决策信息有时是以区间数的形式表达的.利用元素两两比较的方法,人们在实践中往往会构造出两类区间数判断矩阵,一类是互反型区间数判断矩阵(考虑元素的重要性程度之比),一类是互补型区间数判断矩阵(考虑元素的重要性程度之差).目前对区间判断矩阵的研究大都集中在互反型的[1-4],而对互补型的研究则相对较少[5-7].这不能满足区间数层次分析法的理论与应用需求.为此,本文提出互补型区间数层次分析的一种排序方法.首先通过构造包含区间数互补矩阵全部信息的等价矩阵族,给出了检验区间数互补矩阵一致性的目标规划方法;然后以区间数互补矩阵的等价矩阵族构造模糊一致性互补判断矩阵为约束,通过优化方法,得到了区间数互补矩阵的权重区间.

2 区间数互补判断矩阵的一致性

为方便,记N={1,2,…,n}.

定义1[8]设矩阵A=(aij)n×n.若有0≤aij≤1,并且aij+aji=1,则称矩阵A是模糊互补判断矩阵.满足以上两者,并且对∀i,j,k∈N,有aij=aik-ajk+0.5,则称A是一致性模糊互补矩阵.

定义2[9]称A=(Aij)n×n为区间数互补判断矩阵,如果它满足

(i)Aii=[0.5,0.5](∀i∈N);

(ii)Aij=A,i≠j;

(iii)Aij=[a,a],0≤a≤a≤1.

引理1 3阶模糊互补判断矩阵A=(aij)n×n为一致性矩阵的充要条件是:a12=a13-a23+0.5.

证用数学归纳法易证,故略.

事实上,上述等式可用矩阵表示为

由于区间数互补矩阵中的元素表示方案的重要性程度之差,因此其中的元素可以唯一的表示成以上形式.对于区间数互反判断矩阵,由于它的元素表示方案的重要性程度之比,因此它被唯一的表示成Aij={x|x=(a)λ(a)1-λ,λ∈[0,1]}[10].

定义3 称矩阵DA={D=(dij)|λij∈[0,1],i,j=1,2,…,n}为区间数互补判断矩阵A=(Aij)n×n, Aij=[a,a]的等价矩阵族.其中dij=λija+(1-λij)a,1＜i≤j≤n,λij∈[0,1],dji=1-dij.

从引理2可知,用此方法表示区间数互补判断矩阵的等价矩阵族是合理的,并且保留了原判断矩阵的所有信息.

定义4 如果区间数互补判断矩阵A=(Aij)n×n,Aij=[,]的等价矩阵族DA中至少包含一个一致性模糊互补判断矩阵,则称矩阵A是一致的.

若矩阵D是模糊一致的,由定理1可知d1j=d1k-djk+0.5,1＜j＜k≤n成立.即

定理2 区间数互补判断矩阵A=(Aij)n×n为一致的充要条件是(2)有解.

证充分性.由于(2)有解,从而存在一组λ=(λ12,λ13,…,λn-1,n)T,使得目标函数成立.由模糊一致矩阵的充要条件知,至少存在一个模糊一致矩阵D=(dij)n×n,即A是一致的.

必要性.由于A=(Aij)n×n是一致的,从而至少存在一个矩阵D是模糊一致矩阵,此时可有λ=(λ12,λ13,…,λn-1,n)T与D对应,即(2)有解.

3 决策模型

由于(2)式有解,即存在一个模糊一致互补判断矩阵,可以利用文献[11]中的排序公式

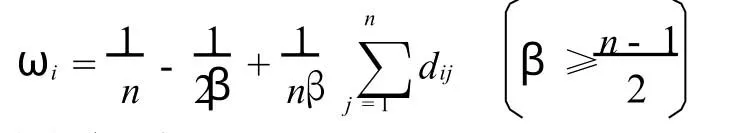
得到模糊互补判断矩阵的排序.代入得到

为求解区间数互补判断矩阵的权重,可构造如下的优化模型.

进而可以用Wi=[minωi,maxωi]表示区间数互补判断矩阵中第i个方案的权重区间,在实际应用中可取β=(n-1)/2.

定理3 若区间数互补判断矩阵A=(Aij)n×n是一致的,则得到权重的任何局部最优解也是全局最优解.

证由于目标函数和约束都是闭区间上的线性函数,从而都是凸集,由文献[12]知,对于凸规划此结论成立.

4 算 例[5]

设对一决策问题,有四个方案x1,x2,x3,x4可供选择,专家在某一准则下利用0.1-0.9标度对决策方案进行两两比较,得到如下的判断矩阵.

利用(3)式的线性规划模型,用MATLAB软件求得各方案的区间权重为

从而由区间数的中心大小,得到方案的排序为x2≻x1≻x4≻x3,此排序结果与[4]一致.

5 结束语

本文给出了一种区间数互补判断矩阵的排序方法.对于区间数互补判断矩阵不是一致的情况,还需要进一步研究.本文对模糊互补判断矩阵的一致性检验,区间数互补判断矩阵的一致性问题的研究有一定的参考价值,同时为进一步研究其排序方法提供了一个思路.

[1] 达庆利,徐泽水.不确定多属性决策的单目标最优化模型[J].系统工程学报,2002,17(1)：50-55.

[2] Stan Lipovetsky,Asher Tishleer.Interval estimation of priorities in the AHP[J].European Journal of Operational Research,1999(14)：153-164.

[3] 王绪柱,刘进生,魏毅强.不确定型AHP判断矩阵的一致性概念及权重[J].系统工程理论与实践,1994,14(7)：16-22.

[4] 吴小欢,覃菊莹,吕跃进.区间数判断矩阵的一致性及权重计算[J].模糊系统与数学,2007,21(5)：113-119.

[5] 徐泽水.区间数互补判断矩阵排序的一种实用方法[J].运筹与管理,2001,10(1)：16-19.

[6] 周宏安,刘三阳.区间数互补判断矩阵排序的一种新方法[J].西安电子科技大学学报(自然科学版),2006,33(2)：292-294.

[7] 黄松,黄卫来.区间数互补判断矩阵的拓扑排序方法[J].模糊系统与数学,2006,20(5)：84-89.

[8] 姚敏,张森.模糊一致矩阵及其在软科学中的应用[J].系统工程,1997,15(2)：54-57.

[9] 吕跃进,王玉燕,覃柏英.区间数的相容性与区间数互补判断矩阵的相容性研究[J].广西大学学报(自然科学版), 2004,29(3)：179-182.

[10] 韦兰用,韦振中.区间数判断矩阵中区间数的运算[J].数学的实践与认识,2003,33(9)：75-79.

[11] 吕跃进.基于模糊一致矩阵的层次分析法的排序[J].模糊数学与系统,2002,16(2)：79-85.

[12] R Horst,P M Pardalos,N V Thoai.全局最优化[M].黄红选译.北京：清华大学出版社,2003.

A New Ranking Method in the Interval Number Complementary Judgement Matrix

S H I Wen-lei, XU Lei
(College of Economics and Management,Hengshui University,Hengshui 053000,China)

By structuring equivalent matrix of interval number complementary judgement matrix,it gets a method for checking the consistency and a new decision making model of interval number complementary judgement matrix.Finally, a numerical example is given to describe the use.

intervalnumber complementary judgementmatrix;consistency;ranking;fuzzy complementary judgement matrix

C934

A

1672-1454(2010)03-0112-04

2007-10-23;[修改日期]2008-01-22

河北省科学技术研究与发展指导计划项目(05457291);衡水学院一般课题(2009029,2009035)