突破点差法解双曲线中点弦问题的难点

●(英山县第一中学 湖北英山 438700)

圆锥曲线的“中点弦”问题，习惯的处理方式是对椭圆和抛物线的问题优先用“点差法”(或说代点相减法)，对双曲线问题优先用“判别式法”(先设出直线方程与抛物线方程联立，消去一元后得到二次方程，然后运用根的判别式等知识求解).但在实际中，许多学生习惯于开始都采用“点差法”，因而在求解某些双曲线问题时，又不得不放弃原来的思路而改用“判别式法”.下面笔者提供2种突破方法,以供参考.

方法1用平面区域思想突破.

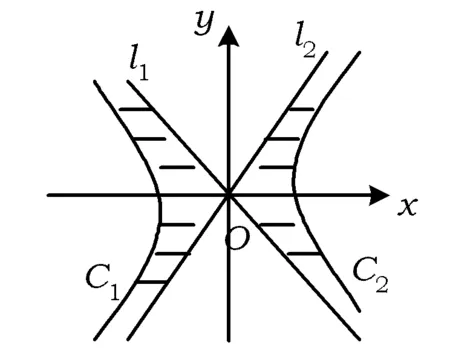
图1

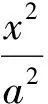
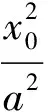
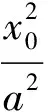
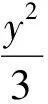
解设A(x1,y1)，B(x2,y2),线段AB的中点为P(x0,y0),则

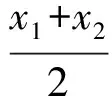
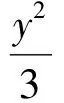
两式相减得

3(x1-x2)(x1+x2)=(y1-y2)(y1+y2)，

即

3(x1-x2)x0=(y1-y2)y0.

因为x1=x2不合题意，所以

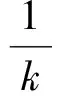
又因为题中的“中点弦”存在，所以

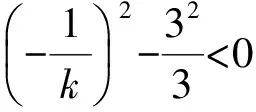
解得k的取值范围是

方法2用回头检验法突破.

即先用点差法求出可能的直线方程，然后与双曲线方程联立，消去其中一个元得到关于另一个元的二次方程，再用Δ检验这个方程是否有解.

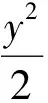
解假设在双曲线C上存在被点M(1，1)平分的弦，弦为AB，双曲线中心为O(0，0)，A(x1,y1),B(x2,y2),则

两式相减得

2(x1-x2)(x1+x2)=(y1-y2)(y1+y2)，

于是

所以直线AB的方程为

y-1=2(x-1)，

即

2x-y-1=0.

2x2-4x+3=0.

由Δ=-8<0,知此方程无实数解，因此假设错误.故双曲线C上不存在被点M(1，1)平分的弦.