基于VAR模型的浙江省老龄化系数预测

邱旭辉 吕盛鸽 (杭州电子科技大学经济与统计研究所,浙江 杭州 310018)

基于VAR模型的浙江省老龄化系数预测

邱旭辉 吕盛鸽 (杭州电子科技大学经济与统计研究所,浙江 杭州 310018)

命题;格兰杰因果检验;向量自回归模型;老龄化系数

老龄化系数指老年人口占总人口的比重。对于老年人口的年龄界限,当前国际上还没有统一标准,本文定义 65岁及以上人群为老年人口。国际上通常认为,一个地区 65岁及以上老年人数占总人口的比例超过 7%(简称为老龄化系数),就意味着该地区已经步入老年型社会。浙江省 1988年就步入了老年型社会(老龄化系数为 7.07%),2008年老龄化系数增长到11.3%,预计未来老龄化趋势将更加严峻。因此,准确预测浙江省老龄化系数的变动趋势,对实现浙江省人口与经济协调发展具有重要意义。

如何准确预测人口数量成为当前人类面临的重要难题之一,国内外学者从不同角度对人口预测模型进行了研究。Lutz等〔1〕建立年龄移算模型,通过设定不同总和生育率水平来预测总人口数;陈爱平〔2〕建立多元回归模型,采用一般回归法、后退法和逐步回归法分别对参数进行估计,从中选取拟合样本精度高的模型进行预测;林芳华〔3〕对马尔萨斯 (Malthus)人口模型作了适当改进,提出可应用于人口预测的 Logistic模型,并用浙江省 1980年～2004年人口数据对模型的预测能力进行了实证检验。年龄移算模型、回归模型等都是常用的人口预测模型,其中年龄移算模型是通过递推移算,一旦参数估计有偏误,将导致模型预测值与实际值的偏差随时间推移而不断增大;人口序列一般都存在自相关现象,且不同序列间很可能存在双向因果关系,以回归模型为代表的单方程模型不能有效表达变量间的双向因果关系。而向量自回归 (Vector Autoregression,VAR)弥补了上述两类模型的不足〔4〕。因此,本文建立人口数量的VAR模型,预测浙江省 2009年～2050年的总人口数、老年人数和老龄化系数。

1 提出命题

任何人口模型的预测能力都是有度的,模型拟合样本精度高也不能无条件地进行长期预测,即使是中长期预测能力较好的 VAR模型,也同样存在着预测的瓶颈。鉴于上述问题,本文在建立 VAR模型之前,先设法估算老年人数的未来变动路径和峰值期,提出判断老年人数中长期变动趋势特征的命题,然后以命题为约束条件建立 VAR模型。

1.1 参考联合国平均预期寿命发展趋势模型,对浙江省 2009年～2050年平均预期寿命进行假定：在 2008年浙江省平均预期寿命 76.81岁的基础上,2009年起每年较上一年增加 0.07岁,当超过 77.5岁时,每年增加 0.02岁。

1.2 根据浙江省 2009年～2050年平均预期寿命、2000年和2005年人口数据推算未来年份各年龄组的死亡概率,编制2000年、2010年、2020年和 2030年人口完全生命表;接着,利用四个生命表的数据估算 2000年 i岁的人平均存活到 t年(t=2030,2031,…,2039)x岁的总生存率 TLPi,x,t,估算公式为：

(i=2 064-t,2 065-t,…,ω -1-(t-2 000);x=i+(t-2 000)

其中 LPi,j,t表示根据 t年生命表估算的 t年 i岁的人平均活到 j岁的生存率,公式为 LPi,j,t=Lit|ljt,Ljt和 lit分别表示 t年生命表中 j岁的平均生存人年数和 i岁尚存人数。

1.3 以 2000年各年龄组实际人口数为预测基数,根据式 (1)的结果估算 2031年～2040年每年进入老年群体人数、老年人口死亡总数和老年人口净增加数,见表1。

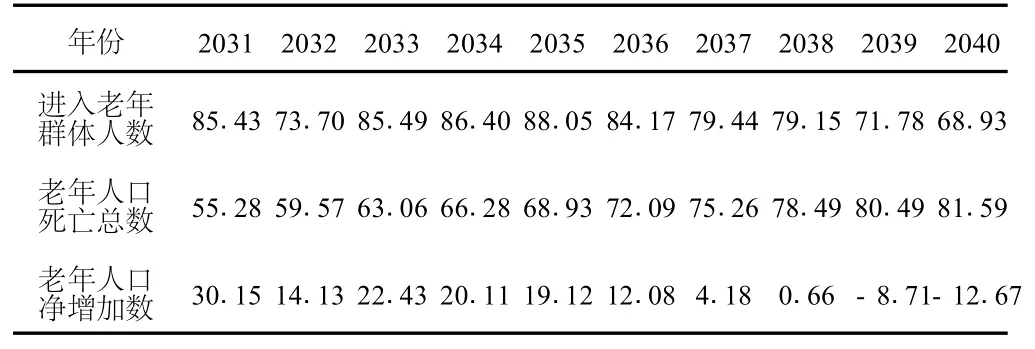
表1 老年人口净增加数变动结果(万人)

表1说明,2031年～2038年老年人口净增加数都为正值,2039年开始老年人口净增加数变为负值。因此,根据表1数据可提出命题如下：

命题：若浙江省 2009年～2050年平均预期寿命按联合国平均预期寿命发展趋势模型进行推算,则老年人口数将在 2038年前后达到峰值。

2 VAR模型

2.1 指标选取及数据说明 结合人口学原理,本文选取总人口、老年人口、男女性别比、总和生育率、死亡率、平均预期寿命和省际净迁入人数 7个指标 ,依次用 y1t、y2t、y3t、y4t、y5t、y6t和 y7t表示 ,用 yj,t-i表示 yjt的 i阶滞后期 (j=1,2,3,4,5,6,7;i=1,2,…)。样本数据为浙江省 1978年～2008年户籍人口数据 (平均预期寿命为常住口径),数据由浙江省公安厅和浙江省统计局提供。

2.2 格兰杰因果检验 为建立被解释变量包括 y1t和 y2t的

VAR模型,先用格兰杰因果检验找出对 y1t或 y2t有显著影响的序列。格兰杰因果检验对滞后期很敏感,所以我们对所有可能的滞后期都进行检验,取相伴概率最小的。在 0.1的显著性水平下 ,y1t、y2t和 y3t两两存在双向因果关系 ,y6t是 y1t和 y2t的格兰杰原因 ,y4t、y7t是 y1t的格兰杰原因 ,y5t不是 y1t和 y2t的格兰杰原因。根据上述分析,在建立 VAR模型时不必考虑我 y5t,只需考虑 y1t、y2t、y3t、y4t、y6t和 y7t。见表2。

表2 格兰杰因果检验结果

2.3 VAR模型

2.3.1 检验模型准则 根据 y1t和 y2t的平均绝对百分误(MAPE)、方程 I和方程 II的调整决定系数 选择模型形式,根据VAR系统整体的赤池信息量 (Akaike Information Criterion,A IC)和施瓦兹信息量 (Schwatz Criertion,SC)选择模型滞后期。其中选择 y和 y的MAPE都比较小、方程 I和方程 II的都

1t2t接近于 1的模型形式,选择 VAR系统整体的 A IC值和 SC值都较小时对应的滞后期。

2.3.2 建立模型 综合格兰杰因果检验结果和人口统计学原理,为预测浙江省总人口数和老年人口数,建立内生变量包括y1t和 y2t的 27个 VAR模型,利用检验模型准则 (见表3)。最终选择以下 3个模型为VAR备选模型：

模型一：内生变量为 y1t和 y2t,滞后 1阶;控制变量为 y3t、y4t、y6t和 y7t,滞后 2阶 ;

模型二：内生变量为 y1t和 y2t,滞后 2阶;控制变量为 y4t、y6t和 y7t,滞后 2阶;

模型三：内生变量为 y1t、y2t和 y3t,滞后 3阶;控制变量为y4t、y6t和 y7t,滞后 2阶 。

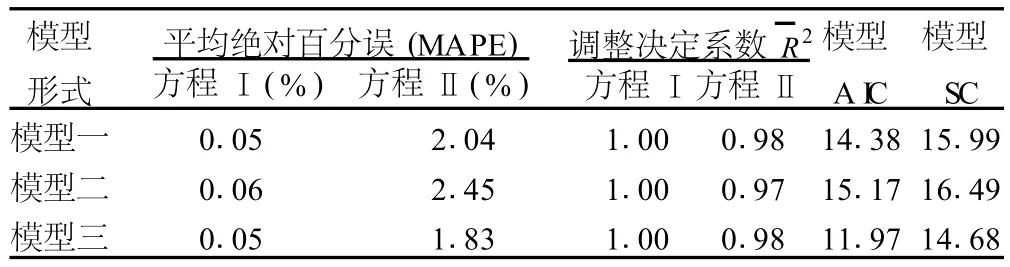
表3 备选 VAR模型检验结果

由表3可见,模型三的各项检验结果都优于另外两个模型,根据检验模型准则,静态预测浙江省 2009年总人口数和老年人口数时,模型三是最优的 VAR模型。由 Eviews软件可得到模型三的方程,即：

2.4 老龄化系数预测

2.4.1 控制方案 控制人口总量增长是当前浙江省人口发展的首要任务,但从中长期来看,为提前应对老年人口高峰,建议考虑逐步放开的生育政策。另外,东部劳动密集型产业向中西部转移的步伐在加快,预计浙江省净迁入人数将呈先增后减趋势。综合上述分析,在 2009年～2050年各年平均预期寿命与命题中假定相同条件下,提出两种方案如下：

方案一：2009年～2015年总和生育率为 1.35,2016年～2029年为 1.40,2030年～2050年为 1.50;2009年～2015年省际净迁入人数每年较上一年增加 0.4万人,2016年开始每年减少 0.5万人,2045年减少至 0后保持不变。

方案二：2009年总和生育率为 1.35,2010年～2019年为1.40,2020年～2029年为 1.60,2030年～2050年为 1.70;对省际净迁入人数的控制同方案一。

2.4.2 预测过程 在方案一下,基于式 (2),用静态法预测2009年总人口数和老年人口数,然后把 2009年预测值作为实际值,重新建立上述 3个 VAR模型,并根据检验模型准则选择最优模型(模型一)静态预测 2010年总人口数和老年人口数,……,重复上面步骤,直到模型趋于稳定,基于合适的模型 (模型二)进行动态预测;最后根据命题选择老年人数在 2038年附近达到峰值的预测结果作为最终结果。在方案二下进行预测时,预测过程类似于方案一。

2.4.3 预测结果分析 两种方案下,分别预测了浙江省户籍总人口数、老年人口数和老龄化系数,部分年份的预测结果见表4。

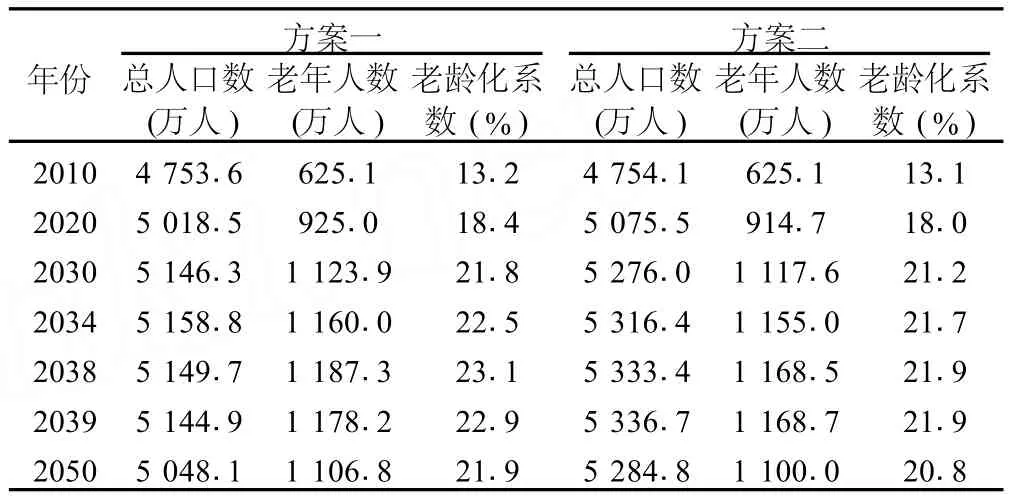
表4 总人口数、老年人数及老龄化系数预测结果

两种方案下预测的总人口数均呈先增后减的变动趋势,分别在 2034年、2039年达到峰值 5158.8万人、5336.7万人,到2050年总人口数分别下降至 5048.1万人、5284.8万人。总和生育率较高的方案,总人口数达到峰值时人口规模越大,峰值以后人口数量下降越慢。与总人口数的变动特征不同,同一年份不同方案下老年人口数预测值相差不多 (相对差距不超过1.6%),且都在 2038年前后达到峰值,峰值期老年人数维持在1168.7万人至 1187.3万人之间。老龄化系数的变动趋势与老年人数基本同步,同样在 2038年前后达到峰值,2020年以后老龄化系数都在 20%以上,最高达到 23.1%,由此可见,浙江省未来老龄化问题十分严峻。

综上所述,总和生育率高,老龄化较容易得到缓解,但老龄化的缓解根本上是由总人口数的提高引起的,预测期内老年人数的变动趋势并未得到根本改变,且总和生育率越高的方案,总人口数达到峰值后人口数量下降越慢,越不利于缓解人口总量对社会经济发展的压力。

1 LutzW,O′Neill BC,Scherbov S.Europe′s population at a turning point〔J〕.Science,2003;299(5675)：1991-2.

2 陈爱平,安和平.中国人口时间序列预测模型的探讨〔J〕.人口与经济 ,2004;6：13.

3 林芳华 (2006).基于消失江省人口模型的研究〔D〕.浙江大学硕士学位论文,2006：5.

4 高铁梅.计量经济分析方法与建模：Eviews应用及实例〔M〕.北京：清华大学出版社,2006：267-80.

C921

A

1005-9202(2010)24-3824-03

国家社会科学基金项目 (09BTJ005);2009年浙江省新苗人才计划-创新项目 (ZX100701040)

吕盛鸽 (1953-),男,教授,主要从事人口统计学研究。

邱旭辉(1985-),男,在读硕士,主要从事数据挖掘方法与应用的研究。

〔2010-08-18收稿 2010-10-16修回〕

(编辑 袁左鸣)