用特征数据表征注采井之间流动单元的一种方法
2010-11-16编译王春艳延长油田股份有限公司勘探部王波延长油田股份有限公司子长采油厂周雄兵川庆工程技术研究院钻井研究所
编译:王春艳 (延长油田股份有限公司勘探部)王波 (延长油田股份有限公司子长采油厂)周雄兵 (川庆工程技术研究院钻井研究所)
审校:纪常杰 (大庆油田工程有限公司)
用特征数据表征注采井之间流动单元的一种方法
编译:王春艳 (延长油田股份有限公司勘探部)王波 (延长油田股份有限公司子长采油厂)周雄兵 (川庆工程技术研究院钻井研究所)
审校:纪常杰 (大庆油田工程有限公司)
提出了一种用注水速率的细微变化来描述注水井和生产井之间流动单元的新方法。该方法可以计算注水井对周围生产井重力因素的影响。重力因素用来描述在生产井周围对生产总值有有效贡献的注水井的影响。小波理论在注水速率方面设计微扰,以便分析生产总值的变化。在注水优化系统中,跟踪注水井对各种生产井的贡献对平衡充填亏空有帮助。另一个是在油藏描述方面的应用,过程所提供的资料可以帮助绘制高渗透流动单元,如孔道和裂缝以及井间流动障碍。该方法已成功地针对模拟线性驱动和拥有各种假设的流动单元及流动非均质性的五点井网条件进行了校准和测试。在一个致密油层水驱实例中,重力因素用来划定引起优先流动的自然裂缝结构。
注采井 注水速率 流动单元特征数据 小波基
1 注入-生产关系
在注水油田中,产量受井底流动压力和注水压力变化的影响。本研究侧重于注水速率变化而引起的改变。为了量化注采井之间的联通程度,估计了代表有效流动单元的重力因素的影响,而这也表明了周围注入流体的影响。
1.1 注入-生产模型
为描述注水速率和产量之间的关系,进行了各种量化系统模型的研究。在本文中,考虑了一般线性有限脉冲响应 (FIR)模型:产量部分由注水速率的FIR滤波型线性组合所确定。也就是说,对于生产井 j的产量部分 Pj(t)来说:

式中,I′ij(t)是注水井 i的注水速率的有限脉冲响应:hij(t)是注水井i和生产井j之间的路径脉冲响应。
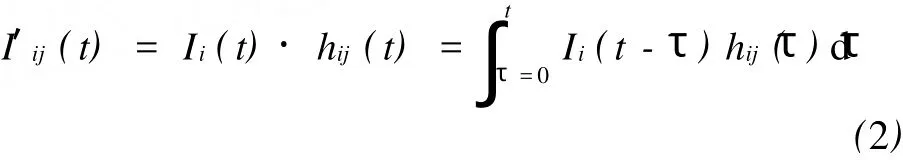
在方程 (1)中,δij是对于注水井i的生产井j的相对重力,如注水井i和生产井j之间估计的有效流动单元。
尽管这是一个线性模型,但是它可用于近似其他研究人员开发的非线性模型。例如,在流线仿真中,应用假想流线描述的注采井之间的关系也可以由此线性模型捕获。由 Yousef等开发的非线性电容模型也可由一种线性模型以离散形式表示,该模型的FIR形状有一些制约因素。
离散形式的模型是:

2 可鉴别信号的设计
假设现在,在适用于注水井的一定的制约因素和限制条件下,我们可以控制系统的输人 (即注水速率)。在实例中,如果把储集层看作一个系统,那么输入就是注水井的注水速率。基于上述模型,目标是设计一系列信号,且每一个信号都容易与其他信号进行区分。在系统工程中,这是一个经典问题。也就是说,去寻找有下列功能的一系列信号:在设置方面,每个信号很容易与这个设置中的其他信号区分。首先探讨信号间的“分辨率”。
最常见和最有利测量的分辨率措施之一是均方差。当且仅当两者之间均方差很大时,两个信号是很容易区分的。因此分辨率的衡量是数量 (为了简便起见,只考虑时间 T内的一系列信号):
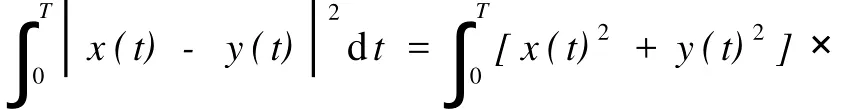
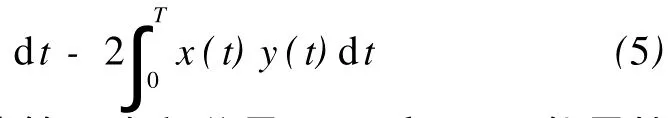
在方程右边第一个积分是 x(t)和 y(t)能量的总和,范围是0≤t≤T。因此,对固定信号能量,y(t)很容易与 x(t)区分,当且仅当:
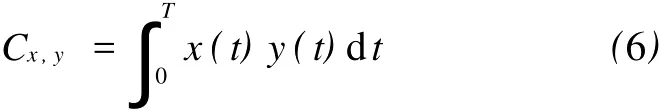
Cx,y是很小的。当 Cx,y值是0时,常常认为x(t)和 y(t)正交。在许多应用中,由于 x(t)和y(t)由不同的路径 (孔道)获得,所以在它们之间可能会有一些时间延迟。因此,该测量值成为
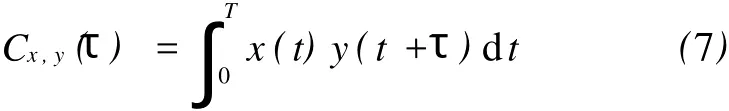
这显然是 x(t)和y(t)的相关函数的幅值。因此,目标变成找到一系列序列,它能显示具有一切可能时间延迟的低相关性。
2.1 Haar小波基
小波分析是一个功能强大的数学工具,它已应用于许多数字信号处理问题。正交小波分解的目的是将任一信号用系列正交信号的线性组合来表示,这就是所谓的小波基。根据正交性质,如果没有时间延迟 (τ=0),任何两个信号都零相关。在本文中,目的是正交小波基的正交性,并从原始的小波基集中找到一个子集,在基本的函数之间即使存在任意时间延迟这个子集中的相关性也是零或接近零。在一个实际油田里,为了执行简便,只考虑最简单的正交小波基,即 Haar小波基,这些基本函数是分段常数 (以便注水速率调整为一系列的恒定值)。在这里,只考虑离散情况。
在离散时间Haar小波分解中,将离散时间信号分解为两个基本函数 h0(n)和 h1(n)的线性组合。

将 h0(n)和h1(n)扩展,可以很容易地获得2L正交Haar小波基。为了研究这些 Haar小波基的分辨率,在本文中首先恢复了对分辨率的公制测量,也就是说,离散关联的两个周期序列 x(n)和y(n):

如果 x(n)和 y(n)有相同时间段,那么 N就是这个时间段。如果它们有不同的时间段,那么N是这两个时间段的最小公倍数。使用此数据时,对于L级 Haar小波基,在从基本集中选择某些特定序列时,可以得到一个子集。在这个子集里,函数之间的相关对于任何时移都是零。这些选定的序列定义如下 (序列是周期性的,N=2L):

这里给出零相关的数学形式:

正如方程表明,所选的 Haar小波基{w1(n),…,wL(n)}形成了一个包含高分辨序列的集,后面将使用选定的序列集构建期望的注入速率序列。请注意,对于一个时期 N=2L,可以得到L序列,在选择L序列的同时,意味着可以区分L注入速率的影响。
2.2 非共线性质
在注水油田中,注水速率和产量是最易获得的数据。许多通过分析注采速率来分析油田特征的程序是不正确的,因为在实际油田日常作业中,注水速率有很强的线性依赖性,这被称为共线问题。在线性估计程序中,共线影响是一个众所周知的问题。一些工具可以测量数据是怎样共线的,这些工具包括相关矩阵、条件数、差额膨胀因子 (VIF)等。根据所有这些数据,可以很容易地表明,所选的 Haar小波基{w1(n),…,wL(n)}可实现最大的非共线。因此,基于选定的 Haar小波基设计的注水速率较之日常作业中的注水速率具有非常好的非共线性。
3 方法
假定可以控制所有注水井的注水速率,那么所需要的就是不时切换注水速率到一系列不同的离散水平。根据一套选定的 Haar小波基,设计了一套注水速率。每个注水速率有一个平均值,这些值是从特定的Haar小波基和一个固定的注水速率项获得的。也就是说,对于注水井 i,注水速率 Ii(t)是:I0i是注水井i的平均注水速率,A是决定与 Haar小波基相对应的 (较小)幅度变化的项。

从零相关出发,如果用一个特定的小波基来修正每个生产速度,那么源于其他小波基的变化将完全消失,仅仅留下具有特定小波基的注水井的影响。为表明这一点,应用以下例子:考虑一个生产井j,其生产速率为 Pj(n)。这里计算 Pj(n)和特定 Haar小波基 wk之间的相关性,其中,相应的注水井为k:

现在,应用 Haar小波基的零相关特性,wk和Ii(n)的相关性可简化如下:

这意味着,与k相比其他注水井的影响将变为零,仅仅剩下 k注水井的影响。因此,方程 (14)变为:
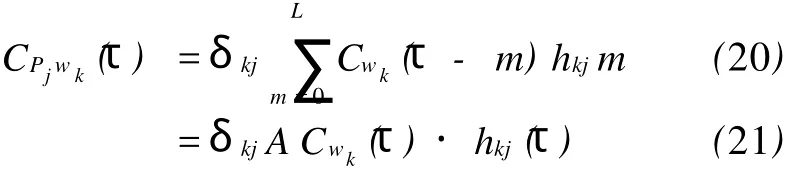
参数δkj是估计的目标,它代表了流体从注水井k到生产井j的质量。虽然唯一的非零项源于注水井 k,但是仍然需要处理 Cwk(τ)·hkj(τ),它是Cwk(τ)的FIR过滤器形式。为了消除其影响,求和了所有带延迟的 CPjWk(τ)绝对值:
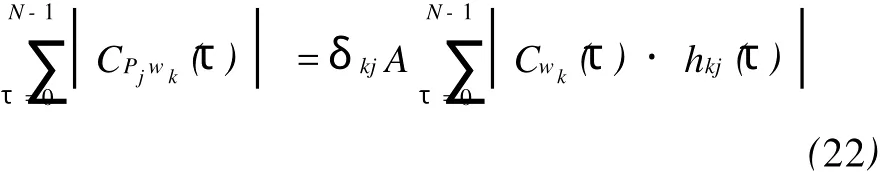
如果滤波器波长L≪N,可以推断:

使用方程 (24),仅仅用产量数据就能够估算δkj的相对值。因此,由δkj表示的有效流动单元可以得到估算。
这里需要讨论与此方法相关的实际问题:在此方法中,注水速率的控制在一个实际油田里是如何影响正常作业的?它的影响程度如何?在实践中,这是一个复杂的问题,因为当改变注水速率时,根据所有储集层的特点,生产速率可能会以一个复杂的方式改变。用平均注水速率 I0i,可以使影响降低到最小。在正常作业下,设置 I0i值为恒定的平均值,在平均值下,希望所有的生产井有变化最小,同时注水井有一些小的改变,从而获得重要信息。
4 结果
在加利福尼亚州,这项技术在简单的流线模型和拥有油田拟合参数的电容模型上进行了测试。然后应用该技术进一步对一个商业油藏模拟器进行了校准。
4.1 流线模型
将方法运用到两种不同的注采井模拟模型中,第一个是流线模型。假设根据一个简单的流线仿真模型,储集层里所有的注采井对与一批假想的流线相连接。任意设置参数,包括每个流线的数量和飞行时间 (TOF)的设置。对于测试,应用自已的设计分配注水速率,然后应用上述方法输出产量。通过对比模拟分配的有效流动单元的估计结果,对这里提出的方法进行了评估。模拟中使用了线性驱动和五点注水井网。
在线性驱动模式中,采用了6口注水井和3口生产井。模拟结果证明,该技术可以在一个简单的流线模拟设置中捕捉高精度的有效流动单元。
在五点注水井网模拟中,采用了5口注水井和4口生产井,其他模拟设置与线性驱动模式的一样。同线性驱动情况一样,该技术在五点注水井网中也可以估测到高精度的有效流动单元。
4.2 拥有油田拟合数据的电容模型
A.A.Yousef等人认为,注采井的关系可近似为“电容模型”。为了验证上述方法,假设注采井的产出关系遵循电容模型。在加州,在实际的注水区块中,给定注水速率和产量,首先通过油田数据拟合找出电容模型的参数,这些参数能捕捉该储集层的一些特点。在确定了所有参数之后,分配注水速率作为输入,并且根据电容模型可以得到所有周边生产井的产量。通过分析这些产量数据,可以估计所有周边注采井对之间的有效单元流量,并且把它们与电容模型参数进行比较 (在电容模型中相对比重λij与有效单元流量有相同的意思)。结果证明,该技术可以准确地估计电容模型中注采井对之间的有效流动单元。
4.3 商业数值模拟器的校准
将方法运用到一个数值模拟器上,采用6口注水井和3口生产井的线性驱动注水模式。在三种情况下,模拟了两个组分——水和油系统,并且仅仅是直井。油的黏度设置为4 mPa·s,数值模拟用天作为时间尺度,即Δn=1 d。
4.3.1 均质实例
这是一个单层均质各向同性油藏,渗透率为100 mD。储集层压力设置为1000 psi(1 psi=6.895 kPa),生产井中的井底压力都设置为800 psi。在观察的中期,改变注水速率的频率,因为希望看到给定不同的注水井不同的注水速率的差异。原始注水井从1到6设置为从最高的频率到最低的频率。在观察的中期,注水井1随注水井4改变它的注入频率,2和5、3和6亦是如此。每半个时期单独分析,图1代表两个半时期的平均值。估计的有效流动单元由箭头代表,它从注水井开始并且指向每个注采井对的生产井。箭头越长,2口井之间有效流动单元的值就越大。

图1 均质实例中估计的有效流动单元
由于储集层是均质的,预期估计的有效流动单元几乎是对称穿过平面,并且随井对之间距离的增加而减小。所有估计结果与选择的储集层条件很匹配。
4.3.2 各向异性实例
单层各向异性储层在 x方向渗透率为10 mD,y方向渗透率为0.01 mD,在储集层中这是一个单一的结构。注水速率和均质实例中的一样,结果如图2所示。
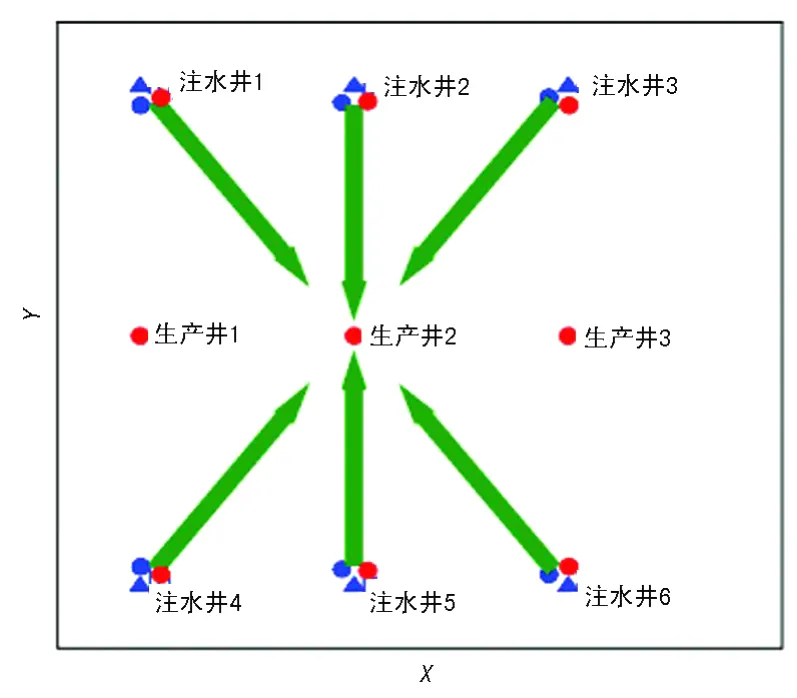
图2 各向异性实例中估计的有效流动单元
由于y方向渗透率非常低,预计大多数的流体将沿 x方向流动。生产井2有一个裂缝穿过它,因此它将获得几乎所有的注入水。结果表明,几乎所有的流动单元都指向生产井2,这个符合预期。
4.3.3 多结构实例
还考虑了渗透率为0.1 mD的单层各向同性储集层,那里有三个不同长度的裂缝。注水速率和前两个实例相同,结果如图3所示。

图3 多结构实例中估计的有效流动单元
在储集层中有三个不同长度的裂缝,并且大约都在45°方位。在该模型中,预期注水井1和注水井4将主要影响生产井1,因为穿过生产井1的裂缝是最长的;注水井2和注水井5对生产井2的影响是次要的;注水井3和注水井6对生产井3的影响是最小的。模拟结果与期望的相吻合。
5 结论
在储集层注采井之间,通过精心设计注水速率和观察周围生产井的产量,开发出一种描述流动单元的技术。
该技术在流线简化模型和与实际数据拟合的电容模型的应用中得到验证。结果表明,该方法可以成功地捕捉到周围注采井之间有效的流动单元。
该技术也得到了数值模拟的验证。通过三个不同的实例进行了评估,结果表明,估计的有效流动单元与每个实例中储集层的特点相匹配。
这技术针对现有分析方法的一些局限提供了一个切实可行的解决方法,提高了估计有效流动单元的精度。这一技术的主要优点是:①由于注水速率为零交叉相关,它能避免注水速率的共线问题;②永远不会得到消极参数。此外,由于其他分析方法是基于已知注水速率的基础之上,该方法将可以与其他方法相配合提高估计的质量。
10.3969/j.issn.1002-641X.2010.8.004
资料来源于美国《SPE 114222》
2009-04-14)
