初探Sylvester方程的解

金晶晶

(福建交通职业技术学院，福建 福州350007)

初探Sylvester方程的解

金晶晶

(福建交通职业技术学院，福建 福州350007)

给出了Sylvester方程AX+XB=C有唯一解的充要条件的一个直接证明，并且给出了该方程相容时的显式解。

矩阵方程；特征值；克罗内克尔直积；Jordan标准型

矩阵方程

0 引 言

1 方程的解的再讨论

由定义1知：A ⊗ B是(m p )× (n p)的矩阵，也可视为是以 aijB为子块的分块矩阵。

定理1 方程（1）有解的充要条件是A与B的特征值满足：

（ 1,...,i m= ， 1,...,j n= ）其中iλ表示A的第i个特征值，jµ表示B的第j个特征值。

方程（1）等价于方程组：

推论1 AX + XB= 0有非零解的充要条件是：存在某个i和 j，有：

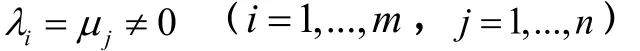
推论2 矩阵方程AX - XB = C 有唯一解的充要条件是：A和B没有公共特征值。

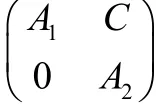
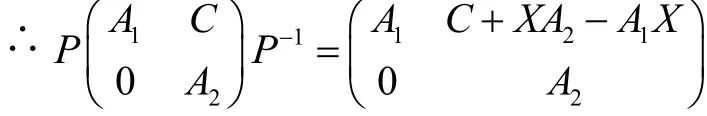
由推论2可知方程： A1X - XA2= C 有唯一解X，这个解X所确定的P就使得：

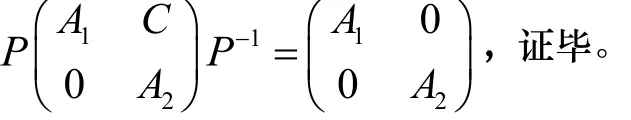
定义3 若函数矩阵 A( x )= (aij(x ))m×n的所有各元素 aij(x) （ i = 1,...,m， j = 1,...,n）都在[a , b]上可积，

则称 A( x)在[a , b]上可积，并且：

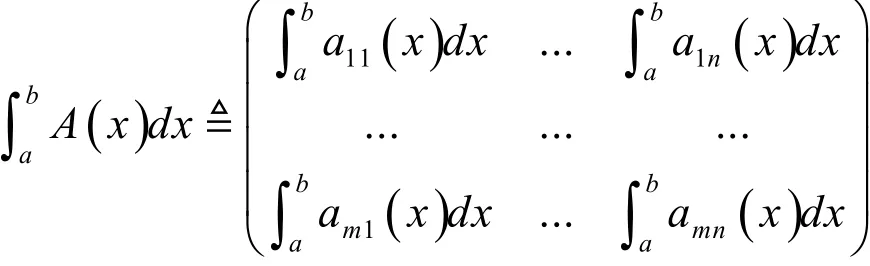
证：考虑方程：

由[8]中第11章知： ()AtBtY t e Ce= 。

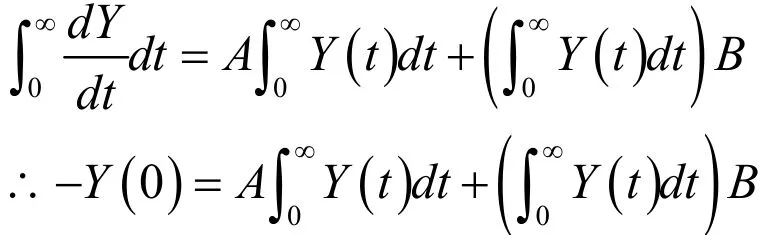
即

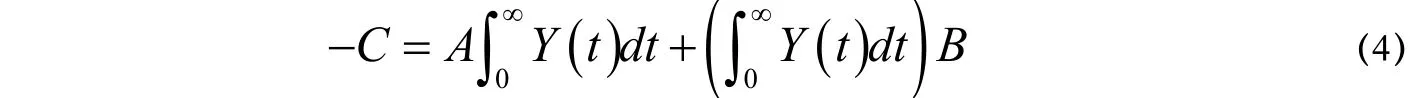
证毕。

2 方程的显式解

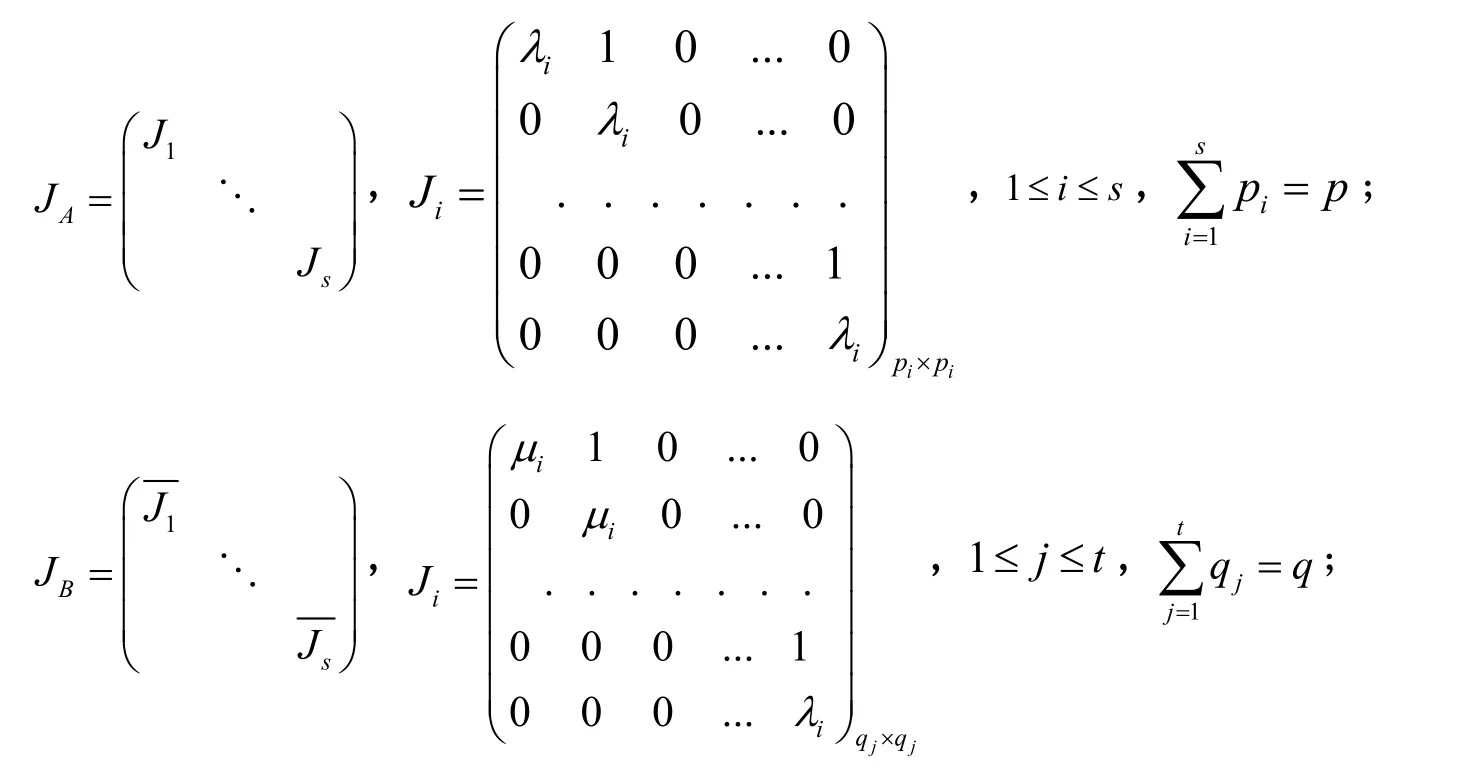
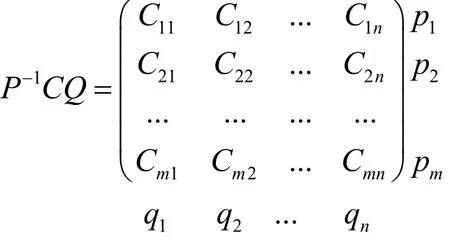
令

显然， Dij(t)中每个元素都是多项式，其次数不超过 mi+ nj- 2。因此有：

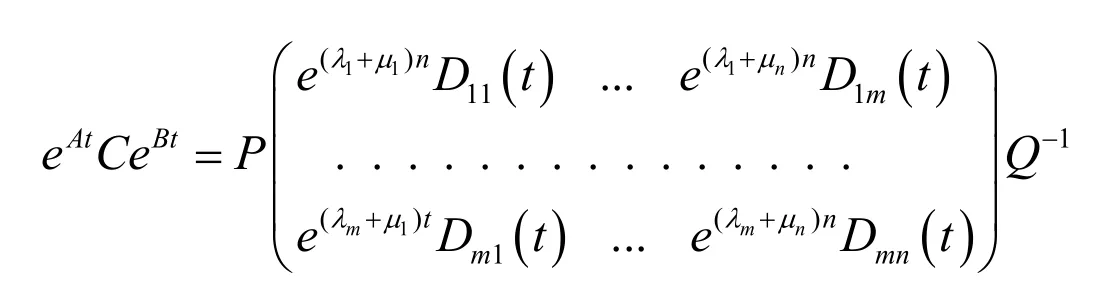
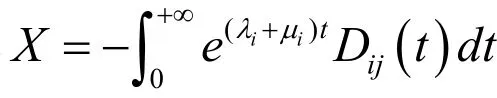
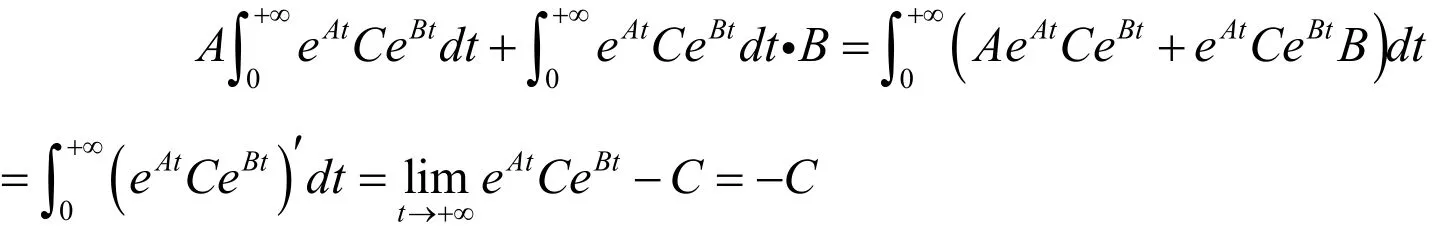
同理可得：

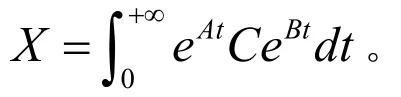
[1]须田信英.自动控制中的矩阵理论(曹长修译)[M].北京：科学出版社,1979.

[2]慕德俊,戴冠中.利用并行方法解AX+XB=C型线性矩阵方程[J].自动化学报,1966.

[3]刘畔畔,李庆春.矩阵方程AX+XB=C的对称解及其最佳逼近[J].江西师范大学学报,2009.

[4]蒙世奎,矩阵方程AX+XB=F的解[J].广西民族大学学报,2009.

[5]Kucěra V. The matrix equation AX+XB=C[J].SIAM J Appl Math,1974.

[6]F.R.Gantmacher,Theory of Matrices,Chelsea Publishing Co,New York,N.Y.,1977.

[7]韩俊林,刘建州.关于几类矩阵的Kronecker和[J].数学理论与应用,2002.

[8]王耕禄,史荣昌.矩阵理论[M].北京:国防工业出版社,1998.

(责任编校：何俊华)

O152.2

A

1673-2219（2010）12-0009-04

2010－06－09

金晶晶(1983－)，男，汉族，福州人，理学硕士，助教，研究方向为组合数学与图论。