基于DE算法的隧洞岩爆形迹反分析研究

陈艳香 苏国韶

（湖南科技学院 土木工程与建设管理系，湖南 永州 425100；广西大学 土木建筑工程学院，广西 南宁 530004）

基于DE算法的隧洞岩爆形迹反分析研究

陈艳香 苏国韶

（湖南科技学院 土木工程与建设管理系，湖南 永州 425100；广西大学 土木建筑工程学院，广西 南宁 530004）

差分进化算法(Differential Evolution，DE)是一种基于群体进化的算法，具有收敛速度快、规则简单、易于实现的优点。以一种适用于高地应力条件下的硬岩本构模型为研究对象，提出基于DE算法的参数辨识方法。该方法以破损区的数值计算值与实测值的误差大小作为适应度来评价参数的品质，通过DE算法在全局空间上自适应地辨识该本构模型的最优参数，从而实现对高地应力下隧洞围岩脆性破坏的范围和深度的准确模拟。用该方法对加拿大的Mine-by隧洞进行了围岩本构模型参数识别，计算结果与实测情况相吻合，表明该方法是科学可行的，具有较高的效率和精度。

岩爆；反分析；参数辨识；差分进化算法

随着人类活动向地下空间的延伸，在高地应力区修建的地下工程越来越多。高地应力条件下硬脆性岩体的洞室开挖卸荷导致洞壁应力分异，使储存于岩体中的弹性应变能突然释放，而产生岩爆现象。为保障施工安全，并为洞室稳定支护设计提供可靠的依据，采用数值计算方法准确地预测围岩脆性破坏的范围和深度，意义重大。

目前，国内一些学者采用遗传算法、神经网络等计算智能方法来辨识本构模型，并取得了一定的进展[1～5]，但这些研究均未针对高地应力条件下CWFS硬岩变形破坏特征来开展。为此，针对硬岩本构模型参数难以确定的问题，提出采用基于具有收敛速度快且易于实本文针对现的DE算法的参数辨识方法，即在反分析计算过程中，通过DE算法在全局空间上自适应地辨识该本构模型的最优参数，从而实现对高地应力下地下工程围岩脆性破坏的范围和深度的准确模拟。

1 CWFS硬岩本构模型

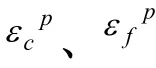
图1 粘聚力、摩擦强度与塑性应变的关系(CWFS模型) [6]

CWFS模型正是基于岩体脆性破坏过程中的粘聚力弱化-摩擦强化的这一重要特征，在 Mohr-Coulomb强度准则的基础上提出的。该模型认为 c、φ是塑性应变的函数其关系见图1，公式如下[7]：

其中，τ为岩体抗剪强度；σn为岩体破坏面上的正应Δε,j=1,3力； 为塑性应变增量；c、φ分别为岩体的粘聚力和内摩擦角； εp为等效塑性应变[7]，且有：

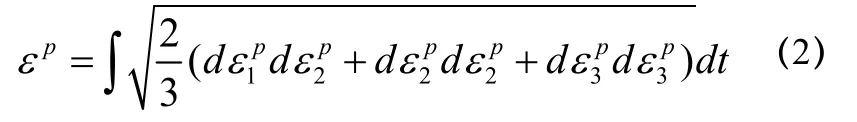
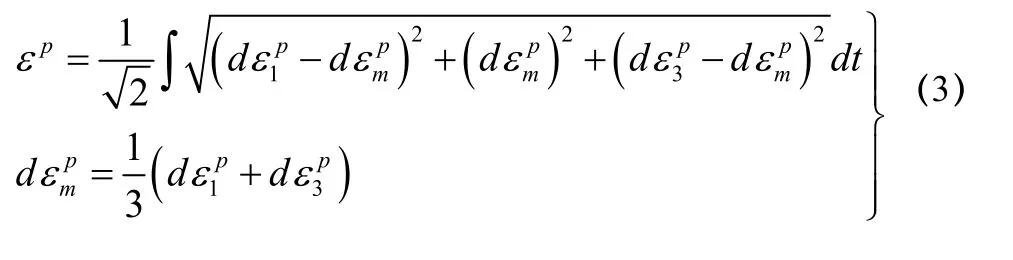
2 差分进化算法

DE算法是由Storn[9]等人于1995年提出的一种进化算法，与微粒群算法(PSO，也称粒子群算法)[10]一样，都是基于群体智能理论的优化算法，通过群体内个体间的合作与竞争产生的群体智能指导优化搜索。DE算法相比传统算法具有如下优点：（1）算法通用，不依赖于问题信息；（2）算法原理简单，容易实现；（3）群体搜索，具有记忆个体最优解的能力；（4）协同搜索，具有利用个体局部信息和群体全局信息指导算法进一步搜索的能力；（5）易于与其他算法混合，构造出具有更优性能的算法。因此倍受学术界的重视，被广泛应用于工程实际中[11～13]。

具体而言，首先对每一个目标向量 iGx ，作如下操作：令：

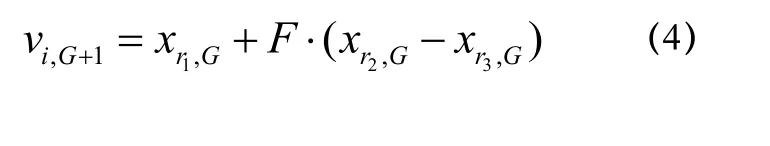
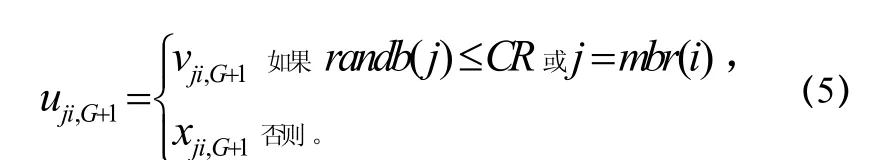
式中， j= 1,2,… ,D ，交叉算子CR∈ (0,1]，randb( j)是产生[0，1]之间随机数发生器的第j个估计量； mbr( i) ∈1,2,… ,D是一个随机选择的序列，用来确保至少从获得一个参数。

3 基于DE算法的CWFS硬岩本构模型形迹反分析方法

该方法的具体步骤为：

（2）建立适应度函数

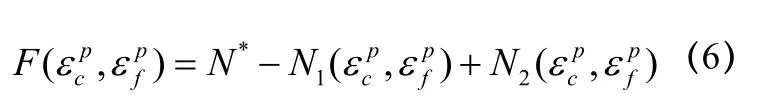
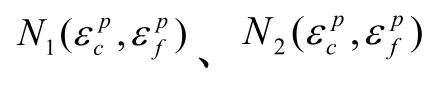
（4）将岩石力学参数和边界条件代入 FLAC3D数值计算模型，通过数值计算，得到每个个体的适应度函数值；

（5）每个个体的当前适应值f与其本身历史上的最佳适应值fid进行比较，若f优于fid，则fid＝f；

（6）将每个个体的最好适应值f与所有个体最好适应值fgd进行比较，若f优于fgd，则fgd＝f；

（7）在种群个数上任意随机选取三个不同整数，再按照公式（4）进行变异操作；

（8）按照公式（5）进行交叉操作；

（9）若满足迭代终止条件（一般为最大迭代次数和种群迄今为止搜索到的最优值满足适应值阈值），停止迭代，输出个体的最佳值；否则，返回（3）。

通过采用FLAC3D中的FISH语言编制CWFS本构模型和DE优化算法程序，一并嵌入FLAC3D数值计算软件，实现了CWFS本构模型的破损区反分析。

4 算例

为了验证本文算法的有效性及计算效率，这里采用下面的工程实例进行研究。

从1982年之后的二十年，AECL公司在加拿大的地下试验室开挖了多条试验洞。其中一洞为椭圆形长轴 6.6m，短轴3.0m，埋深420m，岩石类型为LacduBonnet花岗岩，岩石力学参数见表1。开挖过程中围岩不断地发生脆性剥落破坏，最终形成典型的V形脆性破坏区，见图2。若不考虑受圆洞底板上方堆积的废石渣自重作用，底部与顶部破坏区分布应是对称的。实测地应力为：σ1=60±30MPa，σ2=45± 4MPa，σ3=11±2MPa，其中σ1与σ3之间的夹角为11°。

表1 LacduBonnet花岗岩力学参数

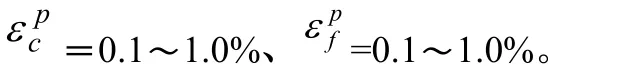
采用本文方法数值模拟结果见图3，图中阴影部分为破坏区，可以看出模拟结果与实测情况十分吻合。DE算法搜索参数过程和收敛变化情况分别见图4和图5。

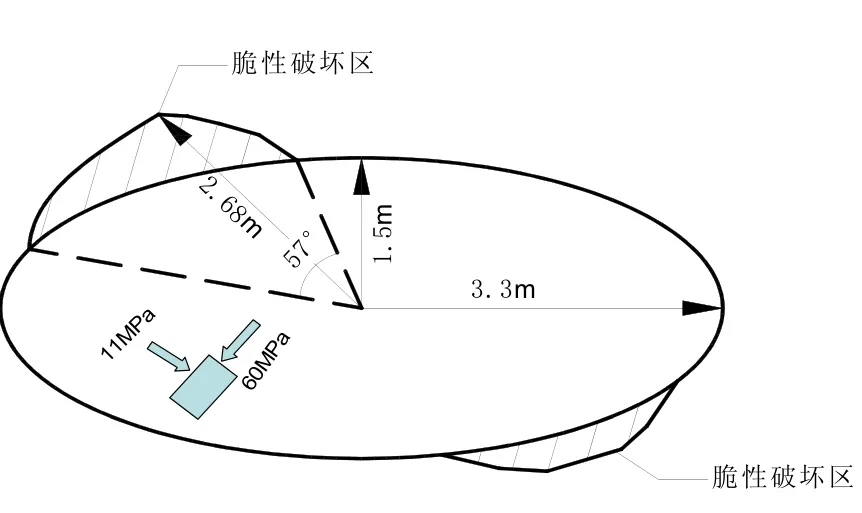
图2 隧洞实测破坏区分布

图3 本文方法模拟结果

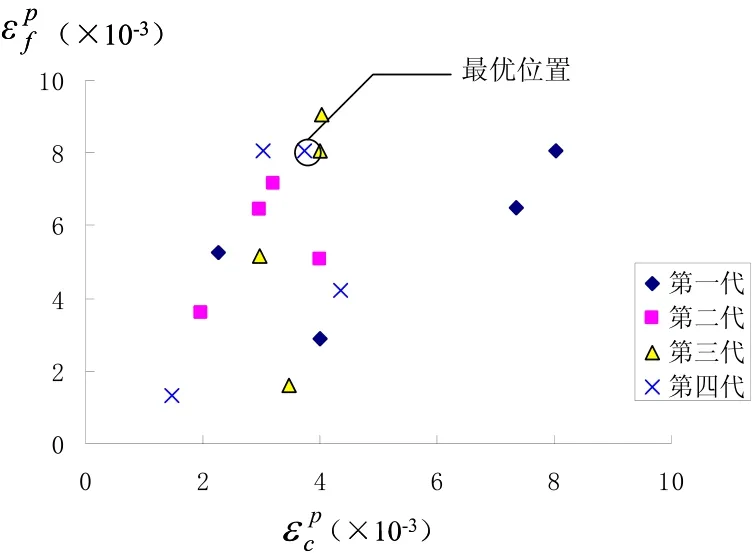
图4 各代粒子的位置变化过程

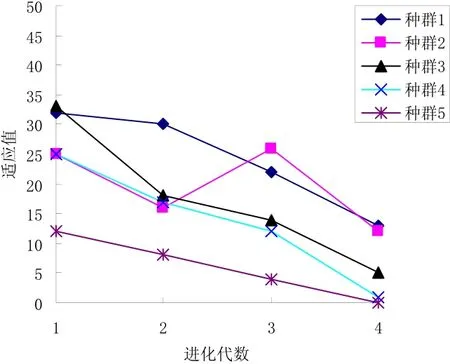
图5 各粒子的适应值变化过程

5 结论

本文提出的基于 DE优化算法的隧洞岩爆形迹反分析方法具有较高的效率和精度，实现了高地应力条件下硬岩脆性破坏区深度和范围的准确模拟。该研究成果对高地应力条件下围岩脆性破损区的预测、支护加固设计，以及安全施工具有重要意义，对其它性质的岩土本构模型的合理参数辨识也具有一定的借鉴意义。

[1]高玮,郑颖人.基于遗传算法的岩土本构模型辨识[J].岩石力学与工程学报,2002,(1):9-12.

[2]高玮,冯夏庭.岩土本构模型智能识别的若干研究[J].岩石力学与工程学报,2002,(S2):2532-2538.

[3]樊琨,刘宇敏,张艳华.基于人工神经网络的岩土工程参数反分析[J].河海大学学报,1998,(4):98-102.

[4]孙道恒,胡俏,徐灏.力学反问题的神经网络分析法[J].计算结构力学及其应用,1996,(3):308-312.

[5]王卫华,丁德馨.开采沉陷反分析的神经网络方法研究[J].南华大学学报,2001,15(1):10-14.

[6]Hajiabdolmajid V, Kaiser P K. Brittleness of rock and stability assessment in hard rock tunneling[J].Tunnelling and Underground Space Technology,2003,18(1):35-48.

[7]Y.H.Hao. R.Azzam. The plastic zones and displacements around underground openings in rock masses containing a fault[J].Tunnelling and Underground Space Technology,2005,(20):49-61.

[8]Itasca Consulting Group Inc.,FLAC3D(version2.1)[M]. Itasca Consulting Group Inc,1997.

[9]Storn R, Price K. Differential Evolution——A Simple and Efficient Adaptive Scheme for Global Optimization over Continuous Spaces[R].Berkeley:ICSI,1995,(8):22-25.

[10]苏国韶,冯夏庭.基于粒子群优化算法的高地应力条件下硬岩本构模型的参数辨识[J].岩石力学与工程学报,2005,(17):3029-3034.

[11]周艳平,顾幸生.差分进化算法研究进展[J].北工自动化及仪表,2007,(3):1-5.

[12]刘波,王凌等.差分进化算法研究进展[J].控制与决策,2007,(7):722.

[13]燕柳斌,陈艳香,苏国韶.岩体弹性模量反分析的进化差分方法[J].广西大学学报(自然科学版), 2008,(4):346-348.

（责任编校：何俊华）

TU415

A

1673-2219（2010）12-0106-03

2010－07－08

湖南科技学院校级课题“基于差分进化算法的深埋隧洞岩体反分析研究”（项目编号09XKYTC016）。

陈艳香（1983－），女，湖南永州人，工学硕士，助教，研究方向为结构优化。