基于累积误差极小值的 SINS初始对准*
2010-11-14吴富梅杨元喜
吴富梅 杨元喜
(1)解放军信息工程大学测绘学院,郑州 450052 2)西安测绘研究所,西安 710054)
基于累积误差极小值的 SINS初始对准*
吴富梅1,2)杨元喜2)
(1)解放军信息工程大学测绘学院,郑州 450052 2)西安测绘研究所,西安 710054)
为了在较短的时间内获得较高的 SI NS初始对准精度,提出一种基于累积误差极小值的初始对准方法。首先给出 SI NS力学编排过程;然后在此基础上导出 SI NS导航误差传播公式;基于速度误差和位置误差公式推导出累积误差与初始对准误差的关系,给出基于载体最后静止时刻累积误差极小值的确定初始姿态角 (航向角)公式。最后用两组实测数据对这种新算法进行验证。结果表明当载体初始对准时间较长时,Kal man滤波精对准和基于累积误差极小值的初始对准方法都可以获得较高精度的对准角;当载体初始对准时间较短时,Kal man滤波精对准精度较低,而基于累积误差极小值的初始对准方法仍可以获得较高精度的对准角。
捷联惯性导航系统;初始对准;航向角;误差极小值;Kalman滤波
1 引言
捷联惯性导航系统 (SI NS)初始对准包括载体位置对准和方位对准。位置对准一般是通过外界辅助设备获得,如由 GPS定位结果获得载体初始位置。方位对准可以通过自对准或外界辅助设备对准获得[1],如磁罗盘或多天线 GPS接收机等。但磁罗盘对准精度较低[2],而多天线 GPS接收机解算复杂[3,4],因此较高精度 SI NS一般采用自对准方式进行初始对准。初始对准误差是影响 SI NS导航或者GPS/SI NS组合导航精度主要的误差源,在导航过程中不易得到正确修正,因此需要严格控制[5,6]。
在捷联惯导初始对准中,影响航向角对准精度的主要因素是陀螺漂移,影响俯仰角和翻滚角对准精度的因素是加速度计偏置。由于陀螺漂移的复杂性和随机性,航向角对准一直是初始对准中的研究难点[5,7]。初始对准包括两个阶段:粗对准和精对准。Kalman滤波是最常用的一种精对准方法。但Kalman滤波获得精确估计的前提是需要可靠的函数模型、随机模型以及足够的对准时间[7,8]。当建立的滤波模型不正确或者模型噪声方差阵不能反映实际噪声时,Kalman滤波的对准精度就会得不到可靠保证甚至滤波会发散[9];当载体初始对准时间较短时,Kalman滤波也许就不能收敛,这样姿态角尤其是航向角的精度就得不到保证[10]。
基于此,本文提出一种基于误差累积极小值的初始对准新方法,有望在较短的对准时间内得到较高的对准精度。
2 SINS力学编排和误差分析
SI NS导航系统是通过力学编排过程将陀螺仪和加速度计观测得到的旋转角增量和速度增量转化为载体运动过程中的位置和速度[11]:
1)计算载体坐标系至导航坐标系的转换矩阵
选取地固坐标系 (WGS84)为导航坐标系。通过陀螺仪测得的角度变化率扣除地球自转角速度经过四元数的更新[11],可以得到载体坐标系至导航坐标系的转换矩阵那么载体坐标系至当地水平坐标系(东北天坐标系)的转换矩阵为:

2)计算载体的位置和速度
由加速度计测得的是采样间隔Δt里载体坐标系中相应于比力的速度增量,需要通过转换矩阵转换成导航坐标系中的速度增量:

那么,载体的速度增量为[7,8]
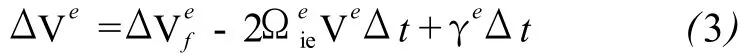
经过积分,载体的速度和位置分别为:
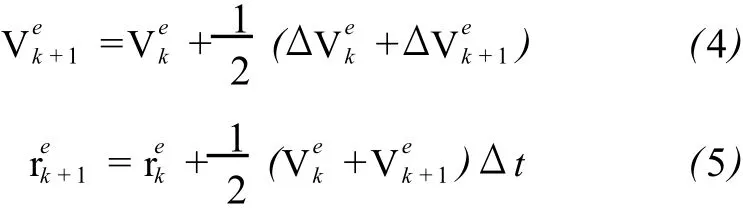
3)误差分析
对式(3)微分,可得载体速度增量的误差:
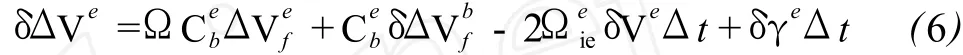
其中,Ω为真实转换矩阵与计算的转换矩阵之间失准角误差ε的反对称阵,为加速度计观测误差,δVe为由当前速度引起的误差,δ γe为正常重力向量误差。
位置增量误差为

其中,δ是积分误差。
3 基于累积误差极小值的 SINS初始对准
在获得精度较高的姿态角之前,需要通过粗对准获得载体的粗略姿态角[12]:
1)粗对准
重力加速度 g和地球自转角速度ωie在当地水平坐标系(东北天坐标系)中的各分量分别为:
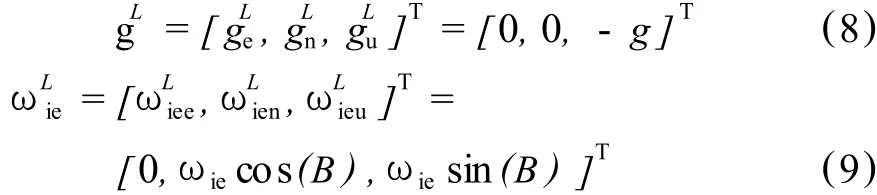
其中,B为地理纬度。
由 gL叉乘可构成一个新向量γL,即:

静基座下载体坐标系中,理想情况时陀螺仪和加速度计的输出信号是和 gb,由和 gb叉乘也可得到γb,根据姿态矩阵可得到:
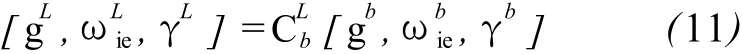

如此可获得 3个姿态角 y、p和 r的概略值。
因为陀螺仪和加速度计的输出信号包含陀螺漂移、加速度计偏置以及各种其他误差源的干扰,粗对准获得姿态角误差较大,因此需要对粗对准结果进行精确校正。Kalman滤波算法是最常用的一种精对准方法[7,8],但是应用这种算法需要有足够的对准时间(不少于 5分钟)和可靠的状态噪声和观测噪声矩阵。当这两个前提得不到满足时,Kalman滤波获得高精度对准结果就很难保证,尤其是对准时间少于 5分钟时,Kalman滤波结果也许就不会收敛。
初始对准俯仰角和翻滚角主要受加速度偏置影响,在 Kal man滤波精对准过程中,收敛速度较快;而航向角主要受陀螺漂移影响,收敛速度较慢,在较短的时间内很难获得高精度的对准精度。因此下面主要针对对准时间较短、初始航向角误差较大的情况,提出一种精对准方法。
2)基于累积误差极小值的精对准
由分析可知,式 (9)中Ω失准角误差矩阵包含两个方面的误差:初始对准误差ε1和开始历元到当前历元的累积误差ε2,其反对称阵分别为Ω1、Ω2。
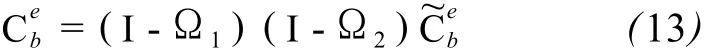
总误差ε的反对称矩阵为:

在载体 SI NS导航过程中,若采用 GPS对 SI NS误差进行周期性校正,则可忽略速度误差δVe、正常重力误差δ γe和积分误差δ的影响。则载体速度和位置误差主要与姿态角误差以及加速度计观测误差有关,即:
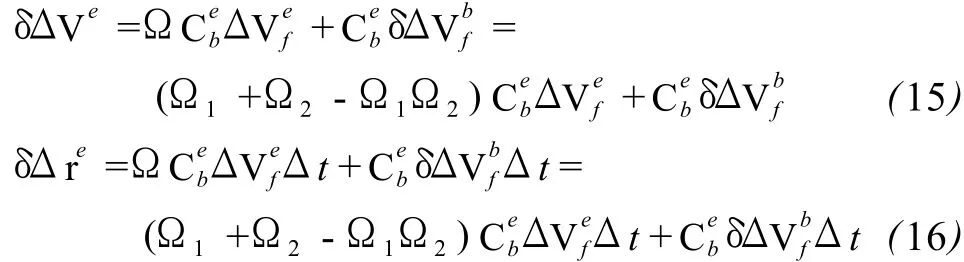
如果Ω1=0,即初始对准无误差,则速度和位置误差主要与导航过程中姿态角累积误差和加速度计观测误差有关。对于精度较高的 SI NS系统,在较短的时间里这两项误差影响比较小而且具有随机性。
如果Ω1≠0,即初始对准存在误差(主要为航向角误差),初始对准角度误差和 SI NS导航过程中累积的姿态角误差会一直影响整个 SI NS导航过程,而且随着时间增长与Ω2增大,Ω2-Ω1Ω2的影响也会越来越大。但是这种误差具有较强的规律性,而且会直接反映到载体最后静止时刻位置和速度的误差上(理想状况下误差真值为 0)。因此可以通过检测SI NS最后静止时刻的导航误差来确定载体的初始航向角。图 1给出了不同的初始航向角对 SI NS单独导航结果的影响 (9.6°为正确值)。从图 1中可以看出:(1)当载体处于初始静止时刻,由于系统尚不稳定,不能用初始静止时刻的误差作为检测的标准;(2)当载体处于最后静止时刻,航向角误差影响较大,并且呈线性增大;(3)航向角在载体运动时刻也有影响,但是由于载体运动的复杂性,误差不能表现出规律性。因此,可以针对航向角误差对导航误差影响的特点(2)作为确定初始航向角的条件。
假定粗对准航向角为 y0,真实航向角在区间[y0-θ°,y0+θ°]之间,取 y1=y0-θ°,yk+1=yk+α2θ°,当

yk就作为真实初始航向角的估计值。
对这种初始对准方法进行分析可知:
1)该方法是一种在事后重新确定初始航向角的方法,适合于事后高精度数据处理,在实时导航时不适用;
2)为了得到较高的对准精度,需要较高精度的SI NS系统。
4 算例与分析
采用两组 GPS/I NS组合导航数据对上述初始对准方法进行验证。
算例 1:取一组 GPS/I NS车载导航数据。I MU采样频率为 100 Hz,GPS数据采样周期为 1.0 s,组合周期为 1.0 s。载体初始静止时间约 5分钟。初始位置 X、Y、Z坐标分别为 -2 271 358.223 m、5 008 107.342 m、3 220 377.609 m。
算例 2:取一组 GPS/I NS机载导航数据。I MU采样频率为 200 Hz,GPS数据采样周期为 1.0 s,组合周期为 1.0 s。载体初始静止时间约 2分钟。初始位置 X、Y、Z坐标分别为 4 275 902.267 m、649 200.954 m、4 672 778.929 m。
算例中,θ=5°,α=0.01。下列参数由经验确定:陀螺仪和加速度计误差相关时间分别为 600 s与 600 s;陀螺仪和加速度计初始均方差分别取 10. 0°/h和100μg;初始位置误差为5 m、5 m、7 m;初始速度误差为 0.1 m/s;初始平台失准角误差分别为100.0 s、100.0 s和 500.0 s;采用松组合方式导航,观测量初始方差取 1 m2和 0.01 m2/s2。
采用两种方案进行初始对准:
方案 1:Kaman滤波初始对准;
方案 2:基于累积误差极小值的初始对准;
图 2和图 3给出算例 1中利用 2分钟静止数据由方案 1给出的初始对准结果。图 4和图 5给出算例 1中利用 5分钟静止数据由方案 1给出的初始对准结果。图 6给出了算例 1方案 2最后静止时刻X、Y、Z方向的位置、速度误差以及总误差随不同初始航向角的变化图。表 1给出了这两种方案初始对准的最后结果。
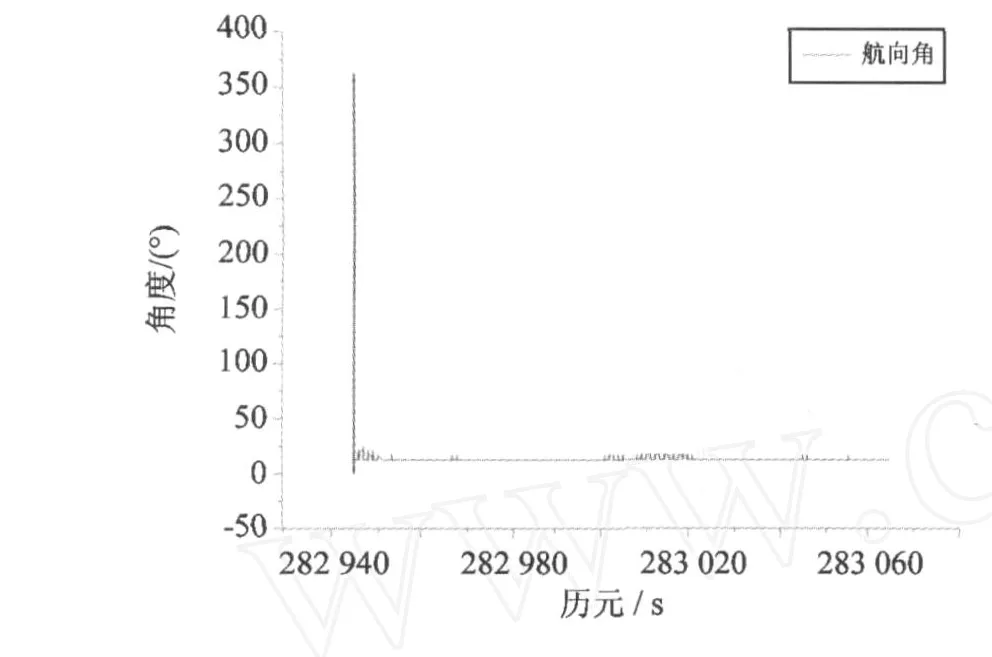
图 2 算例 1,方案 1,初始对准航向角(2分钟)Fig.2 Initial yaw of scheme 1 from data 1(two minutes)

图 3 算例 1,方案 1,初始对准俯仰角和翻滚角(2分钟)Fig.3 Initial pitch and roll of scheme 1 from data 1(t wo minutes)
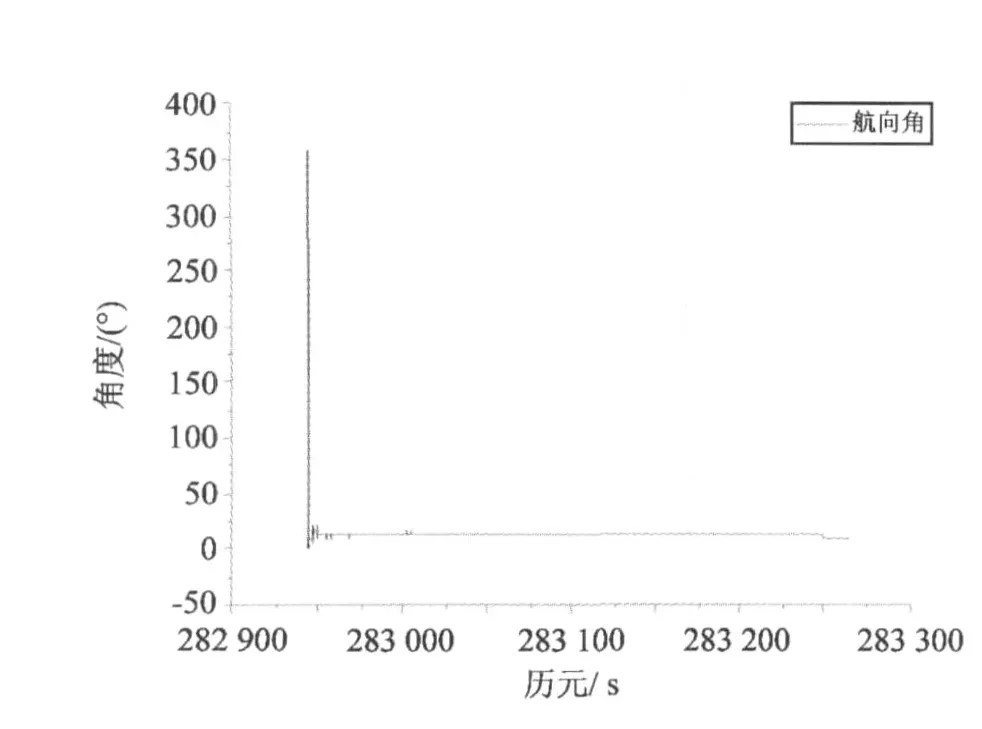
图 4 算例 1,方案 1,初始对准航向角(5分钟)Fig.4 Initial yaw of scheme 1 from data 1(five minutes)
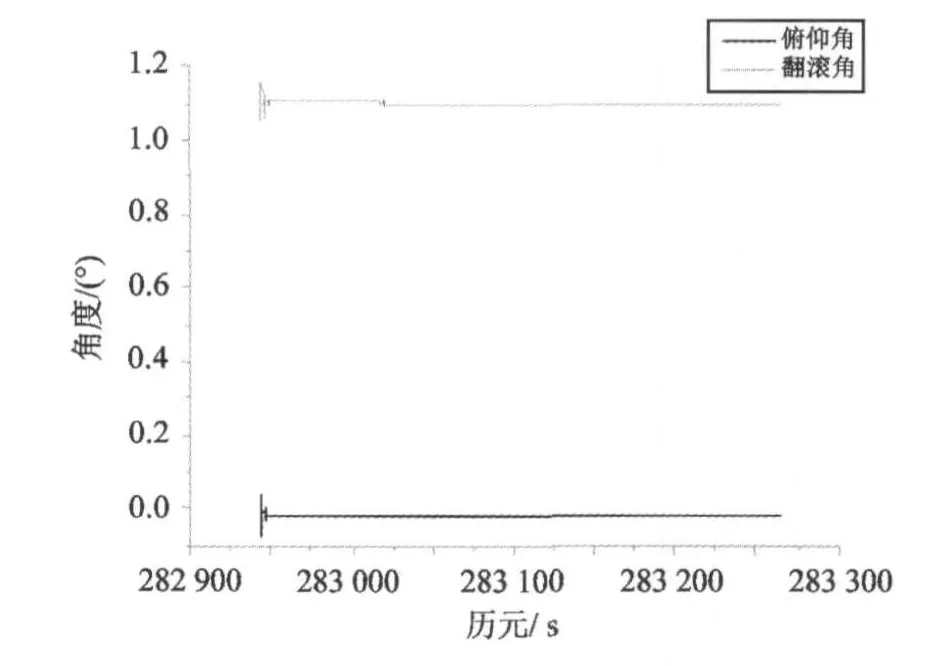
图 5 算例 1,方案 1,初始对准俯仰角和翻滚角(5分钟)Fig.5 Initial pitch and roll of scheme 1 from data 1(five minutes)
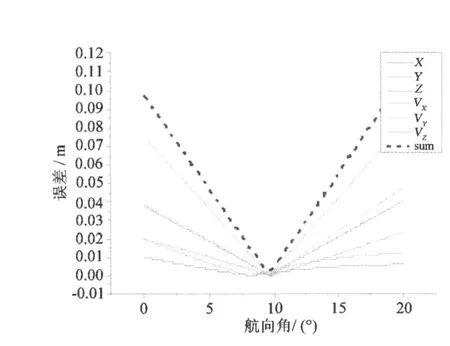
图 6 算例 1,方案 2,初始对准航向角(2分钟)Fig.6 Initial yaw of scheme 2 from data 1(two minutes)

图 7 算例 2,方案 1,初始对准航向角(2分钟)Fig.7 Initial yaw of scheme 1 from data 2(two minutes)

表 1 算例 1,两种方案初始对准姿态角Tab.1 I n itial attitude angles of two schemes from data 1
图 7和图 8给出了算例 2方案 1利用 2分钟静止数据初始对准结果。图 9给出了算例 2方案 2最后静止时刻 X、Y、Z方向的位置、速度误差以及总误差随不同初始航向角的变化。

图 8 算例 2,方案 2,2分钟初始对准俯仰角和翻滚角Fig.8 Initial attitude angles of scheme 2 from data 2(two unites)

图 9 算例 2,方案 2,2分钟初始对准航向角Fig.9 Initial yaw of scheme 2 from data 2(two minutes)
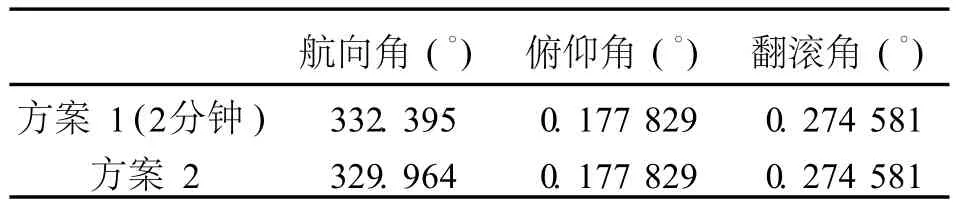
表 2 算例 2,两种方案初始对准姿态角Tab.2 I n itial attitude angles of two schemes from data 2
由计算结果可以得出:
1)由于受陀螺漂移的影响,航向角初始对准需要较长时间,Kal man滤波收敛速度较慢;而俯仰角和翻滚角主要受加速度偏置影响,初始对准时间较短,Kalman滤波收敛速度较快;因此当载体初始初始对准时间较短时,利用 Kalman滤波初始对准,主要会影响航向角的精度,而俯仰角和翻滚角受到的影响较小;
2)当载体初始对准时间较长且状态噪声矩阵可靠时,由 Kalman滤波对准可以获得较高的对准精度;
3)由图 2和图 7可知,当载体初始对准时间较短时,Kal man滤波对准过程中航向角对准精度较低,而俯仰角和翻滚角对准精度较高;
4)当载体初始对准时间较短时,基于累积误差极小值的初始对准方法通过检测载体最终静止时刻的位置、速度以及总误差的局部极小值,可以获得精度较高的航向角。
5)由图 6可看出,由于残留误差影响,位置、速度以及总误差的极小值不会完全一致,这时取总误差极小点时的航向角为载体初始航向角。
5 结论
在 SI NS初始对准过程中,当载体初始对准时间较长且滤波噪声矩阵可靠时,可以通过 Kalman滤波获得精度较高的初始姿态角;当载体初始对准时间较短时,通过 Kalman滤波可以获得较高精度的俯仰角和翻滚角,但是由于受到陀螺漂移误差的影响,航向角收敛速度较慢,对准精度较低;基于累积误差极小值的初始对准方法,可以在较短的时间里获得较高精度的航向角。
1 Godha S.Perfor mance evaluation of low cost MEMS-based MU integrated with GPS for land vehicle navigation application[D].Depart ment of Geomatics Engineering,University of Calgary,Canada,2006.
2 Wang J H.IntelligentMEMS I NS/GPS integration for land vehicle navigation[D].Department of Geomatics Engineering,University of Calgary,Canada,2006.
3 GangLu.Development of a GPSmulti-antenna system for attitude deter mination[D].Departmentof Geomatics Engineering,University of Calgary,Canada,1995.
4 Ji m S.Development of a multi-sensor GNSS-based vehicle navigation system[D].Department of Geomatics Engineering,University of Calgary,Canada,2000.
5 万德钧,房建成.惯性导航初始对准[M].南京:东南大学出版社,1998.(Wan Dejun and Fang Jiancheng.I NS initial alignment[M].Nanjing:Southeast University Press, 1998)
6 袁信,俞济祥,陈哲.导航系统[M].北京:航空工业出版社,1992.(Yuan Xin,Yu Jixiang and Chen Zhe.Navigation system[M].Beijing:Astronautics Industry Press,1992)
7 秦永元.卡尔曼滤波与组合导航原理[M].西安:西北工业大学出版社,1998.(Qin Yongyuan.Kalman filtering and integrated navigation[M].Xi’an:Northwestern Polytechnical University Press,1998)
8 朱利锋,鲍其莲,张炎华.捷联惯导系统初始对准的 H滤波及卡尔曼滤波比较研究 [J].中国惯性技术学报, 2005,13(3):4-9.(Zhu Lifeng,Bao Qilian and Zhang Yanhua.Comparison of Kalman filter and H filter for initial alignment of SI NS[J].Journal of Chinese Inertial Technology,2005,13(3):4-9)
9 Yang Yuanxi,Xu Tianhe and He Haibo.On adaptively kinematic filtering[J].Selected Papers in English of Acta Geodetica et Cartographica Sinica,2001,25-32.
10 聂莉娟.捷联惯导系统初始对准滤波技术研究[D].哈尔滨工程大学,2004.(Nie Lijuan.The research of filter technic in inertial alignment of strapdown system[D].Harbin EngineeringUniversity,2004)
11 董绪荣,张守信,华仲春.GPS/I NS组合导航定位及其应用[M].长沙:国防科技大学出版社,1998.(Dong Xurong,Zhang Shouxin and Hua Zhongchun.GPS/I NS integration navigation positioning and it’s application[M]. Changsha:National Defence Science and Technology University Press,1998)
12 吴富梅,杨元喜.基于小波变换和序贯抗差估计的捷联惯导初始对准[J].武汉大学学报(信息科学版),2007, 32(7):617-620.(Wu Fumei and Yang Yuanxi.SI NS initial alignment based onwavelet transform and sequential robust adjustment[J].Geomatics and Information Science of Wuhan University,2007,32(7):617-620)
A NEW M ETHOD OF SINS INITIAL AL IGNM ENT BASED ONM INIM UM OF CUM ULATED ERROR
Wu Fumei1,2)and Yang Yuanxi2)
(1)Institute of Surveying and M apping,Infor m ation Engineering University,Zhengzhou 450052 2)Xi’an Research Institute of Surveying and M apping,Xi’an 710054)
A new method of SI NS initial alignment based on the mini mum of cumulated error is presented for the situation of short time for initial alignment.Firstly,the mechanization and the error for mulas of SI NS are given. Further more the relation between attitude angles and cumulated errors are deduced based on position error and velocity error for mulas,and the principle of fixing initial yaw angle based on cumulated error checking is given.Finally,two real experiments are carried out to show thatwhen the initial static time is long enough,Kal man filtering and the new method can both bring about good results;butwhen the initial static time is very short,Kalman filtering can not obtain accurate yaw angle while the new method is able to fix the accurate yaw angle.
SI NS;initial alignment;yaw;minimum of cumulated error;Kalman filtering
1671-5942(2010)05-0129-06
2010-04-09
国家自然科学基金(40774001);国家 863计划项目(2007AA12Z331);卫星导航与定位教育部重点实验室(B类)开放基金;信息工程大学博士研究生创新基金
吴富梅,女,1981年生,博士,主要从事动态大地测量数据处理.E-mail:wfm8431812@163.com
P207;P203
A
