基于灰色预测的空间多点残差修正模型研究＊

李晓蕾 刘 睿 田永瑞 谢炳科

(1)重庆科技学院建筑工程学院,重庆 401331 2)中国科学研究院地理科学与资源研究所,资源与环境信息系统国家重点实验室,北京 100101 3)长安大学地质工程与测绘学院,西安 710054)

基于灰色预测的空间多点残差修正模型研究＊

李晓蕾1,3)刘 睿2)田永瑞3)谢炳科1)

(1)重庆科技学院建筑工程学院,重庆 401331 2)中国科学研究院地理科学与资源研究所,资源与环境信息系统国家重点实验室,北京 100101 3)长安大学地质工程与测绘学院,西安 710054)

在分析灰色单点预测模型不足的基础之上,综合考虑变形点之间的空间相关性,提出将残差修正应用于空间多点模型,引入空间多点残差修正模型。对黄河小浪底水利枢纽工程 B断面沉降监测结果的分析表明,该模型整体模拟与预测相对误差绝对值之和 (5个周期)为 122%,优于空间多点模型的 179%与 G M(1,1)模型的284%。同时,短周期数据模拟(5个周期内)相对误差能够控制在 20%以内,具有最好的数据拟合精度。

灰色预测;变形分析;残差修正;空间多点残差修正模型;沉降监测

1 引言

变形分析与预报的常规方法主要包括回归分析、时间序列模型、Kalman滤波模型等,但以上方法适用于观测数列较长,数据信息量大的数据序列,而现代大量工程中经常存在短数据贫信息序列,信息量少、规律性不强,使得上述方法的应用存在较大难度。所以,自从邓聚龙教授提出灰色系统理论以来,由于灰色系统理论提供了贫信息情况下解决系统问题的新途径,为变形监测领域实时、动态、准确地开展变形分析与预报提供了新的手段与方法,因此,灰色系统理论得到了飞速发展[1,2]。

但应用中,灰色单点预测模型准确率不高,严重影响预测结果,因此,本文针对该问题,在分析灰色单点预测模型的不足基础之上,综合考虑变形点之间的空间相关性,引入空间多点残差修正模型,并结合实际工程进行比较分析,得到了比较好的结果。

2 灰色预测模型原理

灰色预测是对本特性灰色系统进行的预测,利用已有的数据资料,建立灰色系统模型,对系统未来的发展作趋势外推,其预测值为一个灰平面区间,且区间大小与预测精度成反比 (图 1)[3,4]。基于灰色系统理论的灰色预测对原始数据没有大样本的要求,通常只要原始数列有 4个以上的数据,就可以通过数据生成变换建立灰色模型 G M(1,1)[5]。

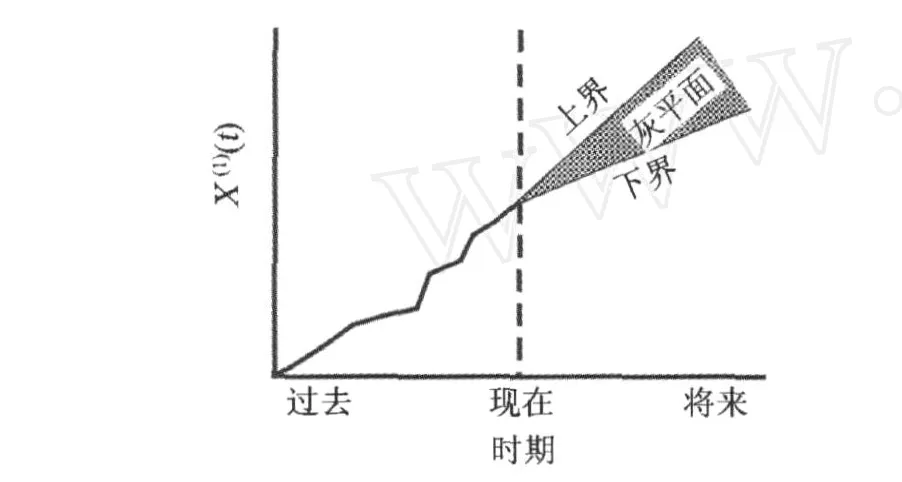
图1 灰色模块示意图Fig.1 Sketch of greymodule

2.1 GM(1,1)模型

若原始数列 x(0)={x(0)(k)}的一次累加生成(1-AGO)数列 x(1)={x(1)(k)}具有明显的指数规律,则可以建立 G M(1,1)模型：

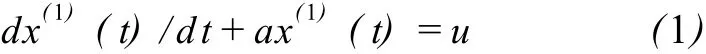
其中:a称为灰色系统的发展系数;u称作灰作用量,是一个内生变量,可以理解为 t时刻,变量 x(t)的变化率 dx(t)/dt与变量本身 x(t)及灰作用量 u的一个线性组合,u是常量,其通解为:

基于时间点 t=0,1,2,…,k,将式 (2)离散化,有:

式(3)为 G M(1,1)模型的离散响应函数,当 k =0,1,2,…,n-1时,得到的(1)(k)为 G M(1,1)模型的拟合值;当 k=n,n+1,…,时,得到的(1)(k)为 G M(1,1)模型的预测值。对(1)(k)做一次累减生成(1-I AGO),即可还原得到原始数列的拟合值与预测值(0)(k),其建模框图如图 2所示。

图 2 G M(1,1)模型建模框图Fig.2 Block diagram ofmodel G M(1,1)

2.2 残差 GM(1,1)模型

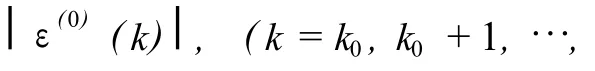
式(6)称为残差修正 G M(1,1)模型。

2.3 灰色预测模型改进思路

G M(1,1)、G M(1,1)以及本文中没有详细列出的 G M(1,N)、G M(2,1)[6]等灰色模型其实质都是针对单点变形的研究,其中 G M(1,N)考虑到了相关点之间的影响,但其仍然是基于单点数据进行预测,没有从整体考虑变形点之间的相互关系。而实际各种工程的变形中,大量的变形监测点间相互影响、彼此关联。抛开这些相互关联的信息,仅仅对单点进行处理与预测,显然不足以反映变形体的整体变形趋势和变形规律。因此,有必要转向多点的空间整体变形分析,充分利用各类采集到的信息,发挥整体积极作用,更接近现实本质的空间动态分析,完整和全面地反映变形体的状况。

3 空间多点残差修正模型研究

3.1 空间多点模型

考虑 n个点相互关联和相互影响[7],对此生成序列建立 n元一阶常微分方程组:

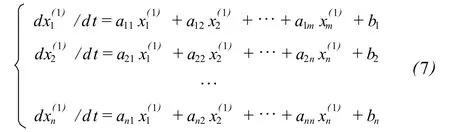
写成矩阵形式:

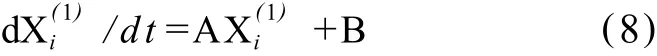
其连续时间响应为[8]：

3.2 空间多点残差修正模型

当 k＜m时,将式(9)离散化得到：

4)将满足残差修正条件的点建立 1-AGO序列代入式 (5)计算其模拟时间序列(k);

5)根据式(6)得到其修正后的时间响应,得出残差修正值;

6)模型精度评定。

4 模型试验与分析

选择黄河小浪底水利枢纽工程大坝B断面的 4个沉降监测数据点 2001—2006年垂直方向位移年变化量作为试验数据(表 1)。以Matlab 7为建模工作环境,综合运用 G M(1,1)、G M(1,N)、空间多点以及空间多点残差修正模型对实测值数据进行模拟与预测。其中前 5个周期数据用于模拟,为模拟值,最后一个周期数据为预测值 G M(1,N)无预测值,全部为模拟值)。经计算,C13与 813点的原始序列不存在 k0满足残差修正模型建立的条件,因此文中仅209与B14点存在空间多点灰色模型修正值。数据结果与对比如表 1与图 3所示。

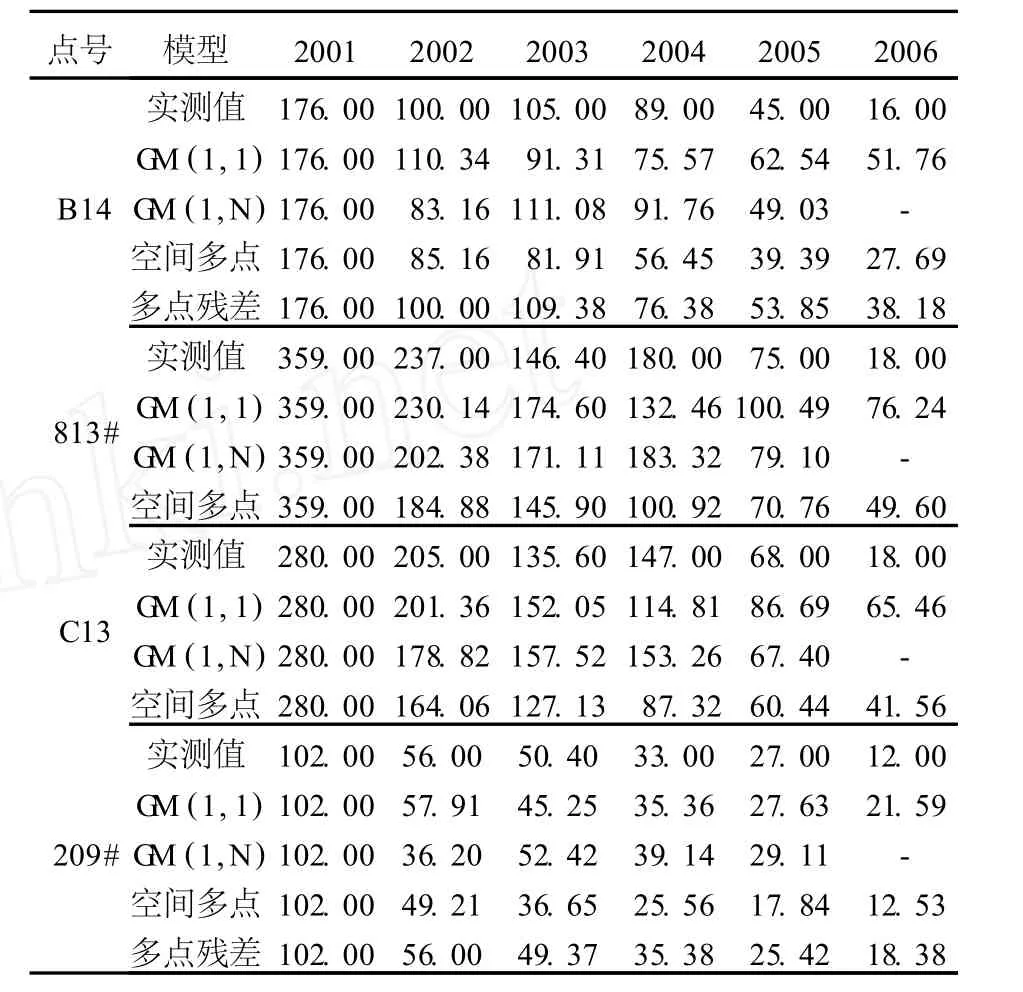
表 1 小浪底大坝 B断面年际沉降监测数据(单位:mm)Tab.1 Annual subsidence mon itoring data of B section of the Xi aolangdiDam(un it:mm)

从表 1与图 3可知：

1)空间多点残差修正模型的数据拟合精度最高,两个点相对误差绝对值之和分别为 38%与15%。同时,相对误差呈现出随周期逐渐增加的趋势,短期内模拟精度最好。

2)G M(1,N)模型的数据拟合精度次于空间多点残差修正模型,变化趋势与空间多点残差修正模型相反,短期内拟合相对误差较大,更适合于长期数据模拟与内插。然其不能应用于数据预测,局限性较大。

3)3种预测模型中,空间多点模型的预测效果最好,其平均相对误差为 96%。空间多点残差修正模型次之,两个点的相对误差平均值为 96%,不如空间多点模型的 39%。G M(1,1)模型的预测精度最差,其相对误差平均值达到了 284%。

4)综合考虑整体模拟与预测精度,空间多点残差修正模型的精度最高,相对误差绝对值之和为122%,空间多点模型为 179%,均远远优于 G M(1, 1)模型的 284%。

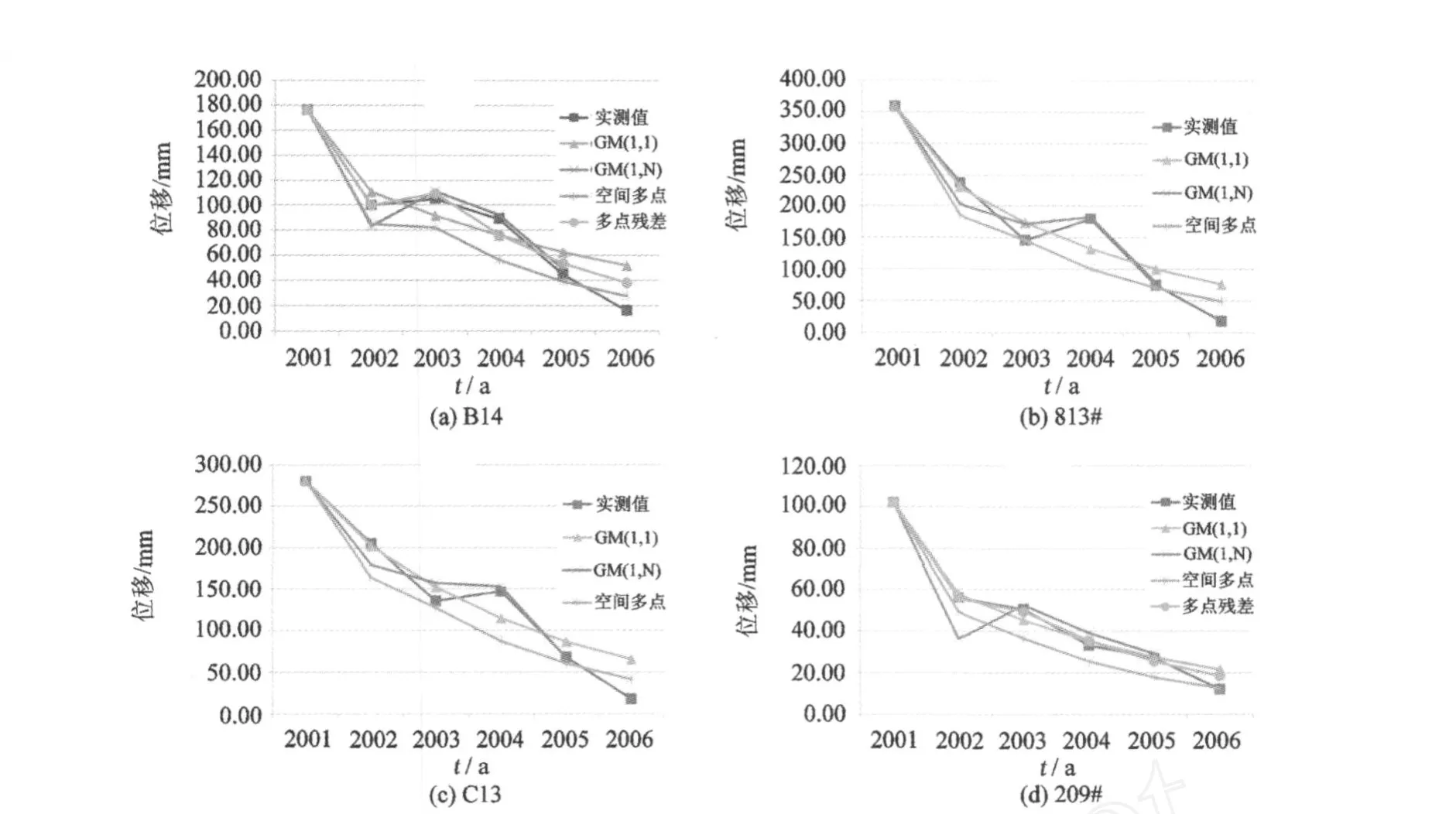
图3 预测结果对比Fig.3 Comparison among the prediction results

5 结论与展望

空间多点残差修正模型的整体模拟预测精度在现有几种灰色系统模型中最好,其整体相对误差绝对值之和为 122%,优于空间多点模型的 179%与G M(1,1)模型的 284%。同时,该模型能够达到很好的数据拟合精度,尤其对于短期数据模拟(5个周期内)相对误差能够控制在 20%以内。空间多点模型数据预测精度略优于空间多点残差修正模型,然而模拟精度远不如空间多点残差修正模型与 G M (1,N)模型。总体而言,多点模型将变形过程作为一个整体的系统进行考虑,该思想代表了变形分析与预报的发展趋势。

空间多点残差修正模型要求数据序列满足残差修正条件,在适用范围方面不如空间多点模型。然而空间多点模型在数据拟合与内插精度上不如 G M (1,N)模型。具体到实际应用中需要多数据多模型综合应用以解决变形监测中的实际问题。同时,考虑到文中数据量以及数据为一次残差修正等限制,作者认为空间多点残差修正模型能够得到更进一步的发展应用。

1 黄声享,尹晖,蒋征.变形监测数据处理[M].武汉：武汉大学出版社,2003.(Huang Shengxiang,Yin Hui and Jiang Zheng.Defor mation monitoring data processing[M]. Wuhan：Wuhan University Press,2003)

2 肖新平.灰色系统模型方法的研究[D].华中科技大学, 2002.(Xiao Xinping.Study of grey system model[D].Wuhan：HuazhongUniversity of Scienceamp;Technology,2002)

3 邓聚龙.灰色系统理论教程[M].武汉：华中理工大学出版社,1990.(Deng Julong.Tutorial of grey system theory [M].Wuhan：Publishing CompanyofHuazhongUniversityof Science and Technology,1990)

4 刘思峰,党耀国,方志耕.灰色系统理论及其应用[M].北京：科学出版社,2004.(Liu Sifeng,Dang Yaoguo and Fang Zhigeng.Gray system theory and application[M].Beijing：Science Press,2004)

5 刘思峰,邓聚龙.G M(1,1)模型的适用范围[J].系统工程理论与实践,2000,20(5)：121-124.(Liu Sifeng and Deng Julong.The range suitable for G M(1,1)[J].Systems Engineering Theoryamp;Practice,2000,20(5)：121-124)

6 陈晓斌,张家生,安关峰.G M(1,1)与 G M(2,1)模型在基坑工程预测中的应用 [J].岩土工程学报,2006,28 (S1)：1 401-1 405.(Chen Xiaobin,Zhang Jiasheng and An Guanfeng.Application of gray-method models G M(1,1) and G M(1,2)forecasting of pit excavation engineering[J]. Chinese Journal of Geotechnical Engineering,2006,28 (S1)：1 401-1 405)

7 潘国荣,刘大杰.顾及邻近点变形因素项的动态模型辨识及预测[J].测绘学报,2001,30(01)：32-35.(Pan Guorong and Liu Dajie.Dynamic modeling identification and predication in consideration of the adjacent point deformation [J].Acta Geodaetica etCartographica Sinica,2001,30(1)：32-35)

8 王穗辉,潘国荣.基于MATLAB多变量灰色模型及其在变形预测中的应用 [J].土木工程学报,2005,38(05)：24-27.(Wang Suihui and Pan Guorong.A Matlab-based multi-variate grey model and its application in deformation prediction[J].China Civil Engineering Journal,2005,38 (5)：24-27)

STUDY ON SPATIAL M ULTI-PO INT RESIDUAL MODEL BASED ON GREY PRED ICTION

Li Xiaolei1,3),Liu Rui2),Tian Yongrui3)and Xie Bingke1)

(1)School of Civil Engineering and Architecture,Chongqing University of Science and Technology,Chongqing 401331 2)Institute of Geographical Sciences and Natural Resources Research,Chinese Academy of Sciences,Beijing 100101 3)College of Geology Engineering and Geom atics,Chang’an University,X i’an 710054)

On the basisof the analysisof the shortage of Grey single-pointpredictionmodel,by considering the spatial correlation between the deformation observation points,the residual modification is applied in the spatial multi-pointmodel and thus the spatialmulti-point residualmodel is developed.By taking the subsidence monitoring data of Xiaolangdimultipurpose dam as an example,the results shows that the total absolute values of relative error (5 cycles)of spatialmulti-point residualmodel is122%,better than 179%of spatialmulti-pointmodel and 284% of G M(1,1)model.Meanwhile,thismodel has the best fitting accuracy with the relative error less than 20%in short-cycle fitting.

grey prediction;defor mation analysis;residual modification;spatial multi-point residual model;subsidence monitoring

1671-5942(2010)05-0125-04

2010-04-19

中国科学院地理科学与资源研究所前沿领域创新项目

李晓蕾,女,1981年生,硕士,主要从事建筑工程测量理论与应用等研究.E-mail：li.xiaolei8@gmail.com

P207

A