Contourlet域 InSAR干涉图滤波方法研究＊

祝传广 范洪冬 邓喀中 薛继群

(1)中国矿业大学江苏省资源环境信息工程重点实验室,徐州 221116 2)河南理工大学矿山空间信息技术国家测绘局重点实验室,焦作 454000)

Contourlet域 InSAR干涉图滤波方法研究＊

祝传广1,2)范洪冬1,2)邓喀中1)薛继群1)

(1)中国矿业大学江苏省资源环境信息工程重点实验室,徐州 221116 2)河南理工大学矿山空间信息技术国家测绘局重点实验室,焦作 454000)

研究了基于 Contourlet变换的阈值、循环平移干涉图滤波新方法,并与 Goldstein、小波软阈值滤波方法在残差点数目、相干系数均值等方面进行了对比分析。实验表明,新算法对干涉图噪声有很强的抑制能力,较好地保持了干涉条纹的细节,减少了残差点,处理效果好于传统的小波软阈值滤波方法,在某些情况下可与 Goldstein滤波效果相比。

干涉图;时频域;Contourlet变换;阈值;循环平移

1 引言

合成孔径雷达干涉测量技术(InSAR)是通过利用同一地区的多幅 SAR复图像获得的地形相位信息,反演地形高度或地表形变。实际应用中,多幅SAR影像间一般间隔时间较长,地物的变化、大气的变化都会使干涉图存在不同程度的失相关,在干涉图中产生噪声误差,致使解缠、生成DEM、探测形变等后续工作难度增加,结果可靠性也随之降低。因此,必须对干涉图进行滤波。目前的主要滤波方法可分为空间域滤波和时频域滤波。空间域滤波有均值滤波[1]、Lee滤波[2]等滤波方法;时频域滤波主要是小波域滤波[3,4]。由于时频滤波方法结合了空间与频率域滤波,具有自动调焦功能,对时间窗和频率窗可做调节：在低频段采用高频率分辨率和低时间分辨率;在高频段采用低频率分辨率和高时间分辨率[5],滤波效果更为明显[6,7]。

InSAR干涉图的小波域滤波方法虽然对噪声有较好的抑制作用,但是由一维小波通过张量积形成的二维可分离小波变换只能表示一维点奇异信息,而不能有效地描述图像中的二维或高维奇异信息,如线、轮廓等[8],而干涉条纹图呈周期变化,轮廓较为分明,采用小波变换对 InSAR干涉图进行降噪处理时,纹理等细节信息并不能很好地得到保留。因此,本文将 Contourlet变换引入到 InSAR干涉图的滤波过程中,该变换既保留了多尺度分析的一些优势,又具有小波变换所不具备的方向性和各向异性[9]。为获取更好的滤波效果,得到高精度的解缠结果,本文研究了基于 Contourlet变换的阈值、循环平移干涉图滤波新方法,并与 Goldstein、小波软阈值滤波进行了对比分析。

2 Contourlet域干涉图滤波方法

2.1 Contourlet变换

Contourlet变换,同小波分解一样,也是一种多分辨率、局域的、方向的影像表示方法。在分解图像时,Contourlet基的支撑区间具有随尺度而长宽比变化的长条形结构,因此,对于细小的有方向的轮廓和线段的表达具有独特的优势[8]。Contourlet变换将图像分解成若干个尺度,在每个尺度上的方向数目(2的整数次幂)可以根据需要自适应的调节,因此, Contourlet变换不仅具有小波的优良时 (空)频分析特征,而且表现出了高度的方向性[10],更适合于进行多尺度的边缘增强处理。Contourlet变换首先是对输入的影像利用拉普拉斯金字塔分解得到一系列的低通子图像和带通子图像,并“捕获”不同尺度上的奇异点;然后,采用方向滤波器组对得到的带通子图像进行方向性滤波,将频域分解成 2j个楔型子带,并将分布在同一方向的奇异点合成为一个系数。通过 Contourlet变换对 SAR图像进行分解时,奇异性特征可以在更多的方向得到自适应的多分辨率刻画,细节在方向子带得到更为显著的呈现[10]。

2.2 阈值去噪

小波阈值去噪的理论依据为：对信号进行变换后,包含有重要信息的系数其幅值较大,但数量少;噪声对应的系数数量多,但幅值小[11]。因此,选择合理的阈值可以获得较好的去噪效果。

同小波变换类似,Contourlet变换具有去相关的特性,使得影像变换后的能量集中在有限的变换域系数上,其余大部分变换域系数的幅值接近于零,而噪声经变换的能量均匀地分布在所有的变换域系数上。最常用的阈值去噪函数有硬阈值函数和软阈值函数公式为[12]：

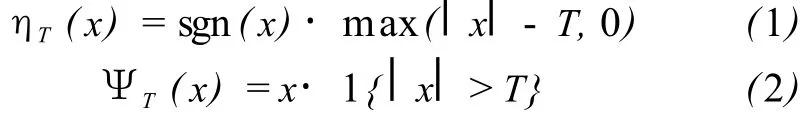
式中,x是 Contourlet变换之后的系数;T是设定的阈值,该值由Donoho[13]所给的方法获取。

2.3 循环平移滤波方法

Contourlet变换由于缺乏平移不变性,阈值去噪后重构的影像在奇异点附近会出现伪 Gibbs现象,因此,采用阈值去噪会在重构的影像中产生虚假成分。为解决这一问题,可以先对原始影像平移一定的距离,然后对平移后的影像进行Contourlet变换得到变换域系数,并进行软阈值去噪,最后对去噪后的系数进行 Contourlet逆变换并反向平移得到滤波后的影像。对于一个给定的平移范围[N1,N2],循环平移去噪算法可表示为[14]:

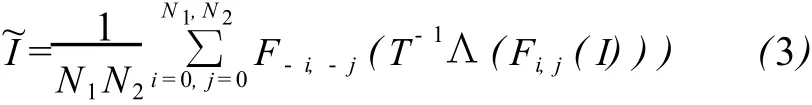
3 干涉图滤波效果评价

3.1 残差点

干涉图中残差点的数目反映去噪效果的好坏,残差点越少,去噪效果越好。残差点的计算方法如图 1[15]：

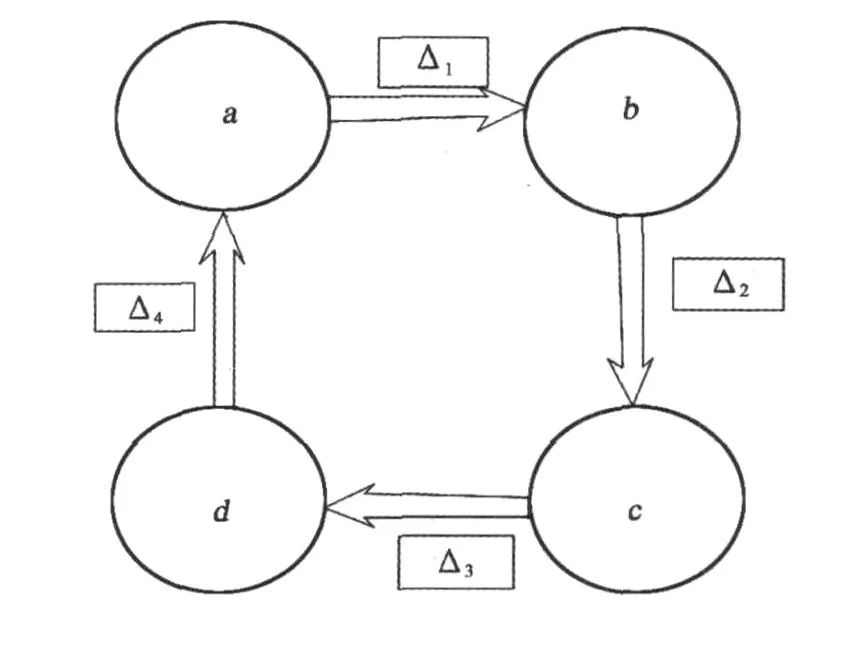
图1 残差点计算路径Fig.1 Route of calculation of residuals

沿箭头所指方向,相邻两像素间求相位差值Δ,然后对Δ求和,即:

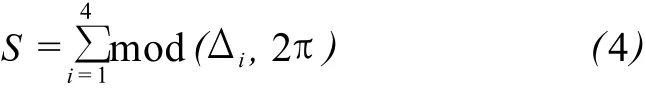
式中,若 S=0,则不存在残差点,否则,存在残差点。对整幅干涉图计算,得到 S≠0的点的总数,即为残差点数。

3.2 伪相干系数均值

伪相干值的高低表明了图像的相干性的好坏,值越大表明相干性越好。计算公式为[16]:

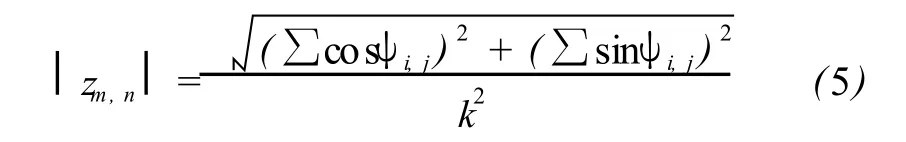
式中,k为窗口大小。计算出每一个像元的伪相干值,即可求得一副干涉图像的伪相干系数均值。

3.3 相位导数均值

相位导数变化计算公式为[16]

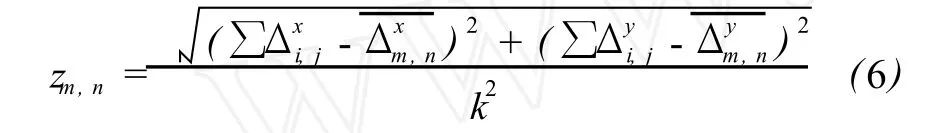
4 实验结果

实验所使用的干涉数据为 ERS1/2影像。第一幅干涉图位于江苏平原地区 (因平原地区高差小,干涉条纹不够明显,实验是针对未去平地效应的干涉图操作的),第二幅干涉图位于青藏高原地区。4景影像均为 C波段,VV极化方式,影像参数见表 1。

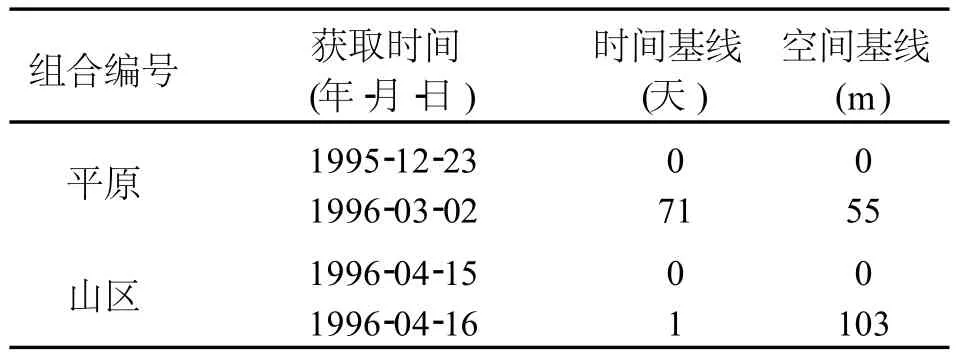
表1 影像参数Tab.1 Parameters of the i mage

Goldstein滤波效果与选取的幂有关,范围一般在 0.4～0.7,幂越大,滤波程度大,但也有可能过度滤波。本文采用Matlab语言实现了所研究的 Contourlet域软阈值及循环平移干涉图滤波新算法,并与Goldstein滤波方法及小波软阈值滤波方法进行了对比,其中,Goldstein滤波方法的幂取 0.5与 0.7。原始干涉图、Goldstein(0.5)、Goldstein(0.7)、DWT软阈值、Contourlet软阈值及 Contourlet循环平移滤波方法获取的干涉图分别见图 2、图 3中的 (a)～(f)。图 3影像大小为 290×290个像元,图 4影像大小为256×256个像元。对干涉图进行了 3层 LP分解,每层的细节方向数分别为 4、8和 16。

由干涉图 2、3可以看出：在平原与山区,本文研究的 Contourlet循环平移滤波方法所得到的结果在清晰度上有明显提高,干涉条纹边缘层次感强,比较连续,均要优于 Contourlet、小波软阈值滤波算法得到的结果;而同 Goldstein滤波方法相比,在不同地形区域时,Contourlet软阈值、小波软阈值及 Goldstein滤波算法则表现出不同的效果。

1)由图 2可以看出,在平原地区,Contourlet软阈值与小波软阈值滤波方法的结果各有优劣：在干涉较差的地区(图框内部),小波软阈值滤波效果要优于 Contourlet软阈值滤波;而在干涉较好的地区(图框外围),Contourlet软阈值滤波则要优于小波软阈值滤波,纹理更为清楚。Contourlet循环平移滤波方法略优于 Goldstein(0.5),而与 Goldstein(0.7)相比则较差。

2)由图 3可以看出,在山区,在地形陡峭 (即条纹密集处,图框内部所示)及平缓区域 (图框外部所示),Contourlet软阈值滤波方法均要优于小波软阈值滤波方法;并且 Contourlet循环平移滤波方法明显优于 Goldstein(0.5),与 Goldstein(0.7)相近,在地形陡峭的区域,甚至优于 Goldstein(0.7)。

滤波后干涉图,从目视角度看,Contourlet循环平移滤波方法在平原地区不如选取适当幂值的 Goldstein滤波方法;但是在山区,Contourlet循环平移滤波方法则要优于 Goldstein滤波方法。

为精确评估几种滤波方法的效果,表 2列出了3种评价滤波效果的指标值。由表 2可以看出, Contourlet滤波及其循环平移滤波方法和DWT方法都能够较好地提高滤波后干涉图的相干性,相干系数得到提高,残差点大量减少,相位导数变化程度得到有效抑制。本文研究的 Contourlet循环平移滤波效果要明显优于 Contourlet软阈值滤波与小波软阈值滤波。并且,目视效果与数据显示一致,即：

1)在平原地区,Contourlet软阈值与小波软阈值滤波方法效果等价,但均不如Contourlet循环平移滤波方法;Contourlet循环平移同 Goldstein(0.5)滤波效果等价,但不如 Goldstein(0.7)。

2)在山区,小波软阈值滤波、Contourlet软阈值、Contourlet循环平移滤波效果依次变好;并且,Contourlet循环平移滤波优于 Goldstein(0.5),同 Goldstein(0.7)相近。

图 2 平原地区各种方法的滤波结果Fig.2 Filtering resultswith differentmethods in the plain area

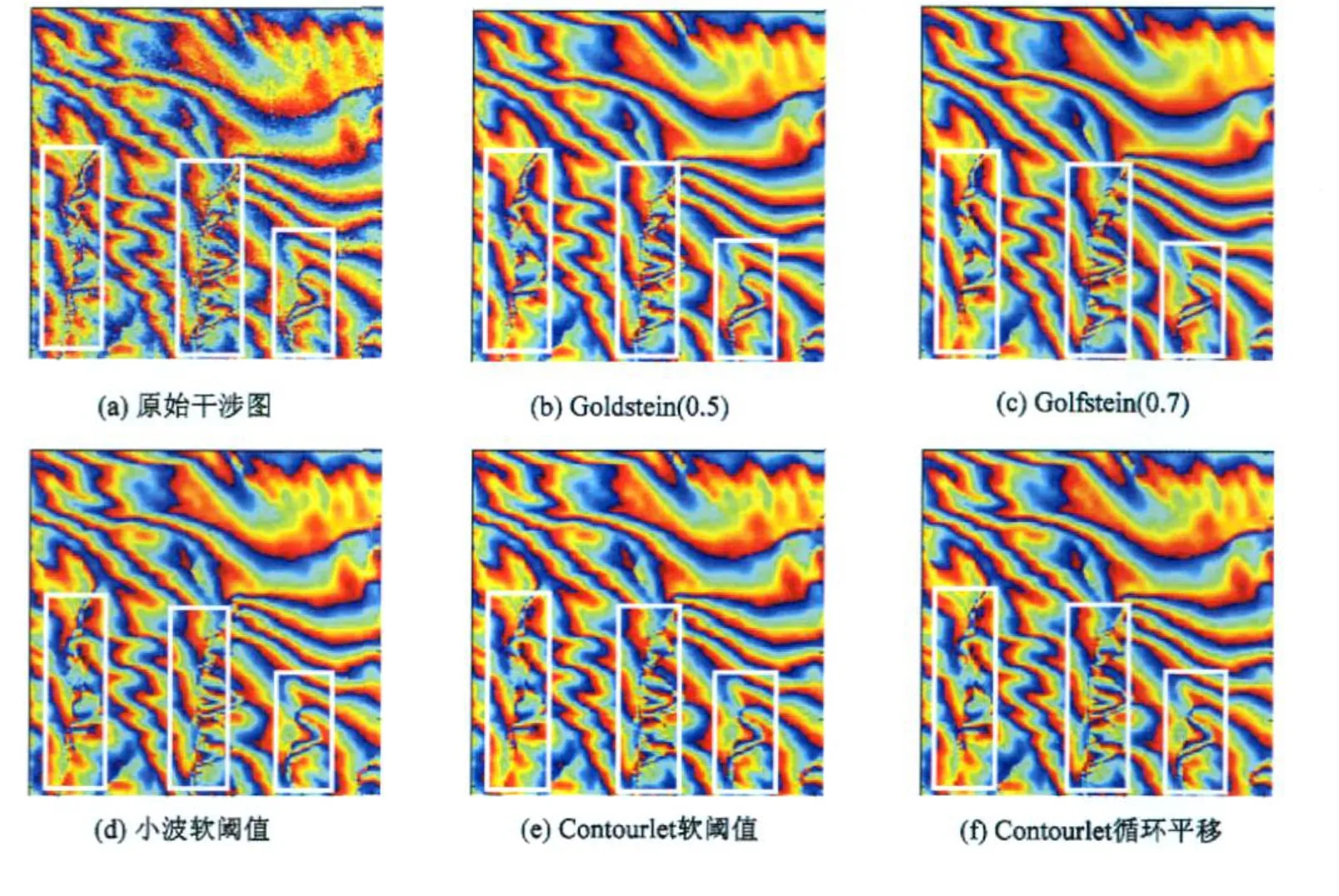
图3 山区各种方法的滤波结果Fig.3 Filtering resultswith differentmethods in the mountainous area

Contourlet循环平移滤波之所以在第二幅干涉图中滤波效果较 Goldstein好,分析原因有：

1)由表 1可见,生成第二幅干涉图的两景影像时间基线仅为 1天,空间基线为 103 m,而第一幅干涉图的两景影像时间基线为 71天,空间基线为 55 m。因此,第一幅干涉图受到的时间失相干较第二幅干涉图严重,而两幅干涉图受到的空间失相干则相差不多。

2)Contourlet的优势在于可以较好描述线、轮廓。在平原地区,轮廓不明显;在山区则不同,地形起伏较大,轮廓非常明显,Contourlet的优势可以得到较好的发挥。

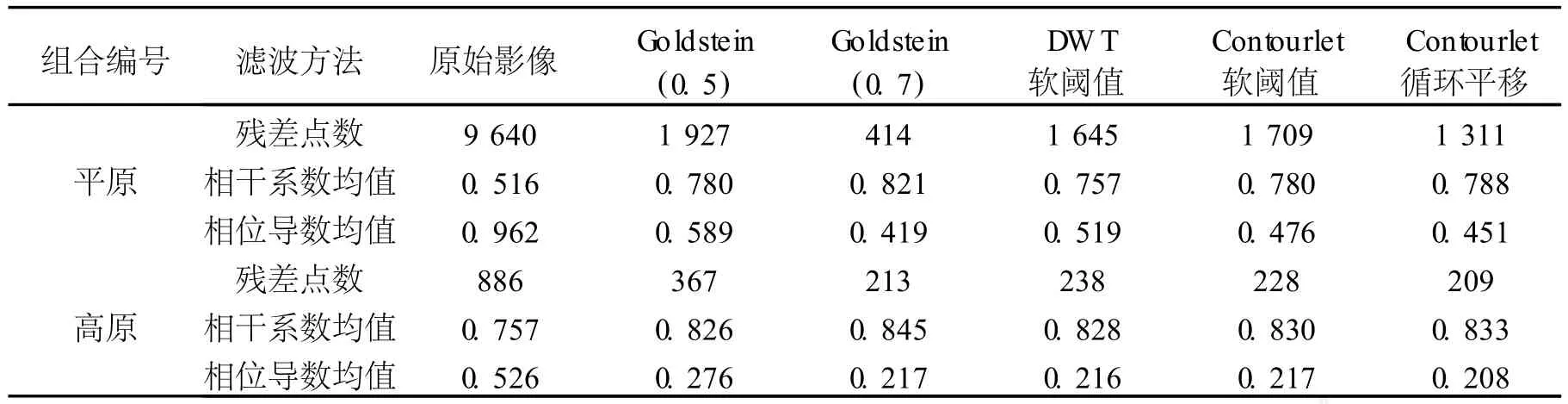
表 2 滤波前后评价指标的比较Tab.2 Comparison between esti mate i ndexes before and after filteri ng

5 结语

将 Contourlet变换引入到 InSAR干涉图的滤波过程中,研究了基于 Contourlet变换的软阈值、循环平移滤波新方法,并与 Goldstein、小波软阈值滤波方法进行了对比。实验表明,Contourlet循环平移滤波在有效去除噪声的同时,较大程度地保留了细节和边缘信息,在高、低相干区域的处理都要明显好于小波软阈值方法,在某些情况下可与 Goldstein相当。为了得到更好的滤波效果,在后续研究中还要对阈值的选取方法、边缘保持、尺度相关去噪等方面做进一步的研究。

1 Eichel P H and Guiglia D C.Spotlight SAR interferometry for terrain elevation mapping and interometric change detection[R].Sand：Sandia Nationl Labs Technology,1993, 2 593-2 546.

2 Lee J S.Digital image enhancement and noise filtering by use of local statistics[J]. IEEE Trans. PAM I,1980, 2(2)：165-168.

3 W itkin A.Scale space filtering：A new approach to multiscale description[A].Acoustics,speech,and signal processing,IEEE InternationalConference on I CASSP’84[C]. IEEE Conferences,1984,150-153.

4 徐晨,等.小波分析应用算法[M].北京：科学出版社, 2004.(Xu Chen,et al.Wavelet analysis and its application algorithm[M].Beijing：Science Press,2004)

5 Mallat S.A theory for multiresolution signal decomposition wavelet representation[J]. IEEE Trans.Pattern Anal. Mach.Intell.,1989,11(7)：674-691.

6 靳国旺,等.InSAR干涉图的矢量分离式小波滤波[J].武汉大学学报(信息科学版),2008,33(2)：132-135.(Jin Guowang,et al.Filtering for InSAR interferograms by vector decomposing and wavelet transfor mation[J].Geomatics and Information Science of Wuhan University,2008,33(2)：132-135)

7 蔡国林,等.小波—维纳组合滤波算法及其在 InSAR干涉图去噪中的应用 [J].遥感学报,2009,13(1)：129-136.(Cai Guolin,et al.Wavelet-W iener combined filter and its application on InSAR interferogram[J].Journal of Remote Sensing,2009,13(1)：129-136)

8 林立宇,等.Contourlet变换-影像处理应用[M].北京：科学出版社,2008.(Lin Liyu,et al.Contourlet transfor mimage precessing and applying[M].Beijing：Science Press, 2008)

9 Do M N and VetterliM.The contourlet transform：An efficient directional multiresolution image representation[J]. IEEE Transactions on I mage Processing,2003,14(12)：2 091-2 106.

10 焦李成,等.智能 SAR图像处理与解译[M].北京：科学出版社,2008.(Jiao Licheng,et al.Intelligent SAR image processing and interpretation[M].Beijing：Science Press, 2008)

11 Donoho D L and Johnstone IM.Ideal spatial adaptation by wavelet shrinkage[J].Biometrika,1994,81(3)：425-455.

12 Chang S C,et al.Adaptive wavelet thresholding for image denoising and compression[J].IEEE Transaction on I mage Processing,2000,9(9)：1 532-1 546.

13 Donoho D L.De-noising by soft-thresholding[J].IEEE Trans.Information Theory,1995,41(5)：613-627.

14 王贞俭.一种 Contourlet循环平移自适应阈值 SAR图像去噪算法[J].电光与控制,2009,16(4)：51-54.(Wang Zhenjian.A contourlet cycle-spinning and adaptive threshold SAR speckle reduction algorithm[J].ElectronicsOptics amp;Control,2009,16(4)：51-54)

15 靳国旺.InSAR获取高精度 DEM关键处理技术研究[D].解放军信息工程大学,2007.(Jin Guowang.Research on key processing techniques for deriving accurate DEM from InSAR[D].Infor mation EngineeringUniversity, 2007)

16 王超,等.星载合成孔径雷达干涉测量[M].北京：科学出版社,2002.(Wang Chao,et al.Spaceborne synthetic aperture radar interferometry[M].Beijing：Science Press, 2002)

STUDY ON FILTERING M ETHODS OF InSAR INTERFEROGRAM IN CONTOURLET DOMA IN

Zhu Chuanguang1,2),Fan Hongdong1,2),Deng Kazhong1)and Xue Jiqun1)

(1)China University of M ining and Technology,Jiangsu Key Laboratory of Resources and Environm ental Infor m ation Engineering,Xuzhou221116 2)Henan Polytechnic University,Key Laboratory of M ine Spatial Infor m ation Technologies,Jiaozuo 454000）

Some new ti me-frequency filtering methods such as threshold,cycle spinning filtering algorithms based on Contourlet transform were studied.After compared and analyzed with the filteringmethods based on DWT (DiscreteWavelet Transform)and the Golstein in the number of residues and the coherence value it can be seen that the new algorithms keep the details of interferogram verywell,reduce more residues,and the filtering effect is much better than the classical soft threshold method based onDWT,and even as good as Goldstein in a certain condition.

interferogram;ti me-frequency domain;Contourlet Transfor m;threshold;cycle spinning

1671-5942(2010)05-0116-05

2010-03-31

矿山空间信息技术国家测绘局重点实验室(河南理工大学,河南省测绘局)开放基金(KLM200909);国家教育部博士点基金(20090095110002);国家自然科学基金(41071273)

祝传广,男,1984年生,硕士研究生,主要研究方向为遥感数据处理及变形监测.E-mail：zhuchuanguang@163.com

P225.1

A