EMD-Wavelet降噪模型在动态变形数据处理中的应用＊

赵玉玲 张兆江 姚习康 刘海新

(1)河北工程大学水电学院,邯郸 056038 2)中煤邯郸设计工程有限责任公司,邯郸 056031)

EMD-Wavelet降噪模型在动态变形数据处理中的应用＊

赵玉玲1)张兆江1)姚习康2)刘海新1)

(1)河北工程大学水电学院,邯郸 056038 2)中煤邯郸设计工程有限责任公司,邯郸 056031)

针对由于多路径等因素的影响,采用 GPS进行动态监测数据精度不能满足变形分析需要的问题,结合小波和经验模态分解(EMD)数据降噪方法,提出一种新的动态变形数据降噪模型 EMD-Wavelet模型。将该模型用于动态坐标序列的降噪处理,通过小波方法对 EMD分解的模态分量进行降噪,EMD对降噪后的模态函数进行重构,得到去噪后的坐标序列。与Wavelet、Kalman滤波、Kalman平滑和 E MD相比较,E MD-Wavelet模型可以得到相对较高的信噪比和最小的均方根差、归一化绝对误差和偏差,表明 EMD-Wavelet模型在 GPS动态变形监测数据处理中相对较优。

EMD;小波变换;降噪模型;动态变形;数据处理

1 引言

作为一种时频分析方法,小波变化具有多分辨率的特征,可以在时间域和频率域反映信号的特征。虽然小波变换适合信号的降噪,但小波基的选取问题限制了其根据信号固有特征将信号分解成不同频率的能力。经验模态分解 (EMD)作为一种新的信号处理工具,在信号趋势提取方面具有很好的应用前景[1],与小波变换相比较,EMD可以较容易地将非线性信号自适应地转换为模态函数。基于 EMD和小波阈值降噪模型,提出了 EMD-Wavelet模型。该模型通过 EMD方法将含有噪声的原始信号分解为模态函数,根据一定的尺度选取标准,选取高频的模态函数进行小波降噪,降噪后的信号的趋势项通过 EMD重构算法得到。利用 EMD-Wavelet模型、Kalman滤波、Kalman平滑、Wavelet和 EMD等 5种模型对信号进行降噪处理,并比较 4个质量评价指标。试验结果表明：相对于其他 4种模型,EMDWavelet模型可以得到比较理想的结果。

2 信号模型

一般来讲,噪声分为测量噪声和动力学噪声[2]。测量噪声是独立于动力系统的,是由测量装置引起的。测量仪器的精度以及将实体转化为数字时都会产生测量噪声。

加法性噪声：噪声与信号大小无关,只具有自身特性,用函数式可描述如下：

可认为,污染输出信号的大小与噪声信号不相关。噪声信号的分布由自身的统计特征决定,也不受信号值大小的影响。

乘法性噪声:乘性噪声信号的输出可认为是由两部分叠加组成:

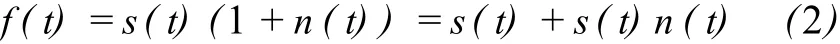
s(t)越大,噪声项越大,通常信号变化范围不大。第二项近似不变,此时,可用加法性噪声模型处理,即假定信号与噪声相互独立。

3 理论基础

3.1 经验模态分解

EMD[3-6]的基本思想是：认为任何复杂的信号都是由一些相互不同的、简单的、非正弦函数分量信号组成。本征模函数 I MF信号需满足以下两个条件：1)待分析信号中的极大点和极小点数之和与过零点的个数之差不超过 1;2)由极大点所构成的上包络线与极小点所构成的下包络线相对时间 t轴对称。本征模函数 I MF两零点之间的每一个波动周期中只有一个单纯的波动模式,没有其他叠加,是EMD中分解信号的基本单元。一维信号的分解可表示为[1,3]：

式中,im fi(t)为所得的 i个 I MF,rn(t)是单调残差函数。

EMD信号处理技术的基本处理步骤如下[1,4]:

1)初始化:r0=X(t)且 i=1。

2)提取第 i个 I MF信号:

(1)初始化:h0(t)=ri(t),k=1;

(2)获取 hk-1(t)的极大值点序列与极小值点序列;

(3)用三次样条插值拟合 hk-1(t)的极值点序列,获得 hk-1(t)的上、下包络线 uk-1(t)和 vk-1(t);

(4)计算上、下包络线的均值曲线 mk-1(t)= (uk-1(t)+vk-1(t))/2;

(5)计算 hk(t)=hk-1(t)-mk-1(t);

(6)如果迭代标准满足则 I M Fi(t)=hk(t),否则 k=k+1并跳转至(2)继续迭代计算。

3)计算剩余信号:ri(t)=ri-1(t)-I M Fi(t)。

4)如果 ri(t)的极值点数大于 2,则 i=i+1并跳转至 2,否则分解结束,ri(t)则为残余信号分量。

信号重构把所有的 I MF信号分量以及参与信号分量相加即可完成。对原始信号完成上述分解步骤后,第 1个 I MF分量 h1(k)中包含有原信号中时间尺度最小的成分,随 I MF阶数的增加,其对应频率成分逐渐降低,余量 ri(t)中则包含频率最低的成分。EMD分解的收敛准则使得分解余量 ri(t)为单调函数,则其周期大于信号的记录长度,ri(t)即为信号的趋势项。

3.2 小波和小波函数

3.2.1 小波变换

式中,t∈R,ψ(a,b)(t)为ψ(t)经过尺度因子 a伸缩、平移参数 b平移构成的子小波,(t)为ψa,b)(t)的复共轭函数,Wf(a,b)为连续小波变换的变换系数。

小波变换分析的结果受小波分析函数的影响很大。本文采用 db2小波函数进行变换分析。

3.2.2 小波阈值降噪模型

若采用分解算法,对信号进行 L级小波变换。由于噪声主要集中在高频信号上,对不同分阶层的高频系数评价计算各自的阈值对小波系数进行阈值处理,对高于阈值的小波系数尽量保留其真实值。而对低于阈值的小波系数赋予 0值,然后进行重构,可获得降噪后的真实信号。选择不同阈值,降噪的效果可能完全不同。根据小波系数阈值量化方法的不同,通常有软硬阈值两种降噪方法：

硬阈值：

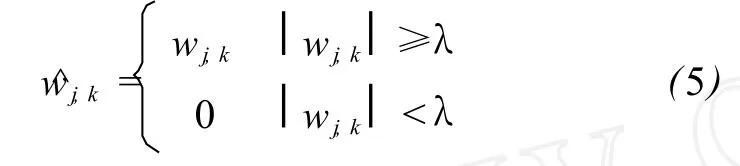
软阈值:

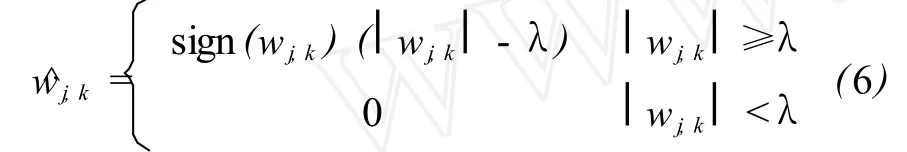
4 EMD-Wavelet降噪模型

通过 EMD方法将含有噪声的原始信号 x(t)分解为模态函数 im fi(i=1,2,…,n),根据一定的尺度选取标准,选取高频的 I MFs进行小波降噪,降噪后的信号的趋势项通过 EMD重构算法得到。

使用 EMD进行信号降噪时,定义如下尺度标准化模量的累积均值[1,2,6]：

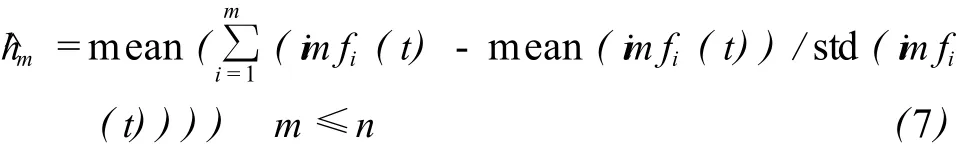
其中,im fi(t)是第 i尺度的模量,如果偏离零值,则从尺度m开始认为是系统的趋势变化所致。降噪后的信号由下式给出:

其中 de(·)为小波阈值降噪。

EMD-Wavelet降噪流程如图 1。

5 质量评价

采用信噪比(SNR)、均方根差 (ERMSE)、归一化绝对误差 (ENAE)和偏差 (EBias)等 4个评价指标,对降噪模型进行质量评价[7-9]。

1)信噪比 SNR反映信号噪声水平,SNR值越大,说明降噪的结果越好,SNR可表示为：

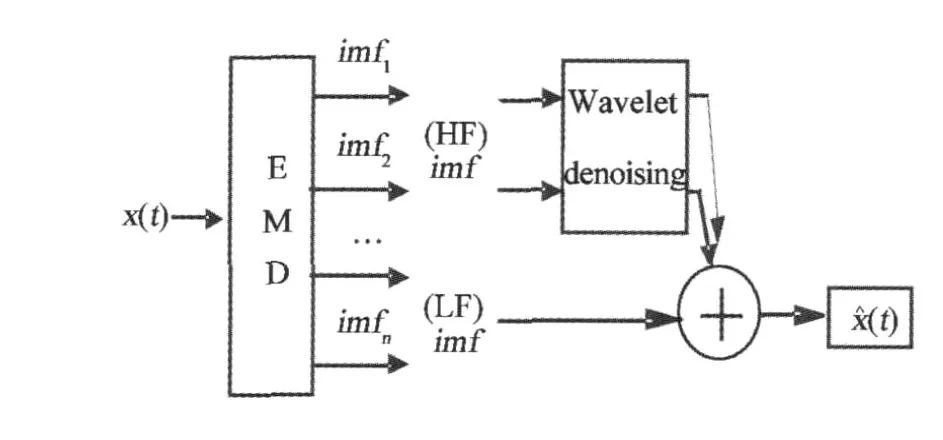
图1 EMD-Wavelet模型降噪流程图Fig.1 Flowchart of EMD-Wavelet noise reduction model

2)均方根差 ERMSE反映降噪后信号对原始信号的平均偏离程度,ERMSE值越小,说明降噪后的信号与原始信号的相似度越高。均方根差定义为:

3)归一化绝对误差 ENAE,将降噪后信号的平均绝对误差对原始信号的均值归一化。ENAE值越小,说明降噪后信号的误差越小,预测无误差时 ENAE值为 0。归一化绝对误差定义为:

4)偏差 EBIas,反映降噪后信号对原始信号的平均系统性的偏离。EBIas值越小,说明偏离量越小, EBIas可以表示为:

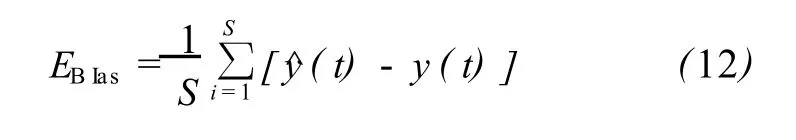
6 数据处理和分析

实验数据为 2009年 2月 28日在河北工程大学某楼顶静态采集的 GPS数据,利用单历元动态解算得到的三维动态坐标 x、y、z方向的时间序列对该楼进行实时动态变形监测 (图 2),采样间隔为 2 s,截取 500个历元进行分析。分离高频 IMFs和低频MFs的标准化模量的累计均值 (MSAM)与尺度的关系,可得 x、y、z方向时间序列分别在m=3、5、7偏离零值,由式(11)确定 x、y、z方向时间序列的高频MFs和低频 IMFs分离尺度为 3、5、7。限于篇幅,以x方向为例说明 EMD-Wavelet降噪过程,对 x方向时间序列进行 EMD分解,可以得到 7个模量和 1个趋势项 (图 3),对依据分离尺度得到的高频 IMFs (MF1, IMF2)进行小波阈值降噪处理,并通过 EMD重构信号,得到 EMD-Wavelet降噪后的信号。

图2 原始 x、y、z坐标序列图Fig.2 Ti me series of originalx,y,zcoordinate

图3 x方向时间序列的 EMD多尺度分解Fig.3 Multi-scale EMD decomposition ofxti me series

利用 Wavelet模型、Kalman滤波模型、Kal man平滑模型和 EMD模型以及 EMD-Wavelet模型进行信号的降噪处理,得到 5种降噪模型下的信噪比(SNR)、均方根差 (ERMSE)、归一化绝对误差 (ENAE)和偏差(EBias)等 4个评价指标 (表 1)。EMD-Wavelet模型的 SNR值在 x方向和 z方向最大,在 y方向略小于 Kalman滤波,同时,EMD-Wavelet模型在 x、y、z方向上的 ERMSE、ENAE和 EBias值最小。利用不同降噪模型得到降噪后的 x方向的信号如图 4所示,噪声在不同程度上得到削弱,图 5给出了去除的噪声部分,EMD模型和 Kalman平滑模型去除的噪声部分相对较大。

7 结束语

实测数据的实验结果表明：EMD-Wavelet模型相对于其他模型明显较优。但 EMD-Wavelet模型参数有时难于确定,其在动态变形的应用中还有待于进一步研究。

表 1 基于不同降噪模型 x、y、z方向时间序列的评价指标Tab.1 Quantitively evaluation ofx,y,zcoordinate ti me series based on different noise reduction models

图 4 基于不同降噪模型的 x方向降噪后的信号Fig.4 Denoised signals ofxwith different denoised models

图 5 基于不同降噪模型的 x方向的去除噪声后的信号Fig.5 Denoised residuals ofxwith different dinoised models

1 Coughlin K Tamp;Tung K K.11-year solar cycle in the stratosphere extracted by the empiricalmode decompositionmethod[J].Advances in Space Research,2004,34：323-329.

2 Flandrin P,Gonçalvès Pamp;Rilling G.Detrending and denoisingwith empirical mode decompositions[R].Eusipco, 12th European Signal Processing Conference,September 6-10,Vienna,Austria.

3 HuangN E,et al.The empiricalmode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[R].Proc.Roy.Soc.,London A,1998,454：903-995.

4 张安兵,等.GPS用于矿区沉陷区地表高精度动态监测的可行性研究[J].煤炭学报,2009,34(10)：1 322-1 327. (Zhang Anbing,et al.Feasibility study on mining surface subsidence high-precisionmonitoring by using GPS[J].Journal of China Coal Society,2009,34(10)：1 322-1 327)

5 戴桂平,刘彬.基于小波去噪和 EMD的信号瞬时参数提取[J].计量学报,2007,28(2)：158-162.(Dai Guiping and Liu Bin.Instantaneous parameters extraction based on wavelet denoising and EMD[J].Acta Metrologica Sinica, 2007,28(2)：158-162)

6 Wang J,Wang J L and Roberts C.Reducing GPS carrier phase errorswith EMD-wavelet for precise static positioning [J].Survey Review,2009,41(312)：152-161.

7 潘显兵.一种改进的小波阈值降噪方法性能分析[J].微计算机信息(测控自动化),2006,22(3)：112-113.(Pan Xianbin.Analysis of an improved methods in wavelet threshold denoising[J].Microcomputer Information(Controlamp; Automation),2006,22(3)：112-113)

8 黄声享,等.GPS动态监测中多路径效应的规律性研究[J].武汉大学学报 (信息科学版),2005,30(10)：877-879.(Huang Shengxiang,et al.Study on the characteristics ofmultipath effects in GPS dynamic deformation monitoring [J].Geomatics and Infor mation Science ofWuhan University,2005,30(10)：877-879)

9 何永红,文鸿雁,袁海莲.基于多小波的变形监测信号处理[J].水电自动化与大坝监测,2007,31(1)：61-71. (He Yonghong,Wen Hongyan and Yuan Hailian.Multiwavelet-based defor mation monitoring signal processing[J]. HydropowerAutomation and Dam Monitoring,2007,31(1)：61-71)

APPLY ING WAVELET EXTENDED EMD NO ISE REDUCTION MODEL TO DYNAM IC DEFORMATION DATA PROCESSING

Zhao Yuling1),Zhang Zhaojiang1),Yao Xikang2)and Liu Haixin1)

(1)Hydroellectrical Institute,Hebei University of Engineering,Handan 056038 2)China Cole Handan Design Engineering Co.,L td.,Handan 056038)

Aiming at the problem that dynamic monitoring data accuracy from GPS can not meet the need of defor mation analysis because of the multi-path and other factors,a new EMD-Wavelet dynamic defor mation data denoising model through the combination ofwavelet and EMD theory isproposed.Firstly,themodel ispresented to reduce noise of coordinate ti me series.Secondly,themodal componentsof EMD decomposition are de-noisedwith the waveletmodel.Finally,the EMD reconstruction gives the extracted ti me series.Compared with the denosingmodels based onWavelet,Kalman and EMD,the EMD-Wavelet model has relatively higher Signal-to-Noise Ratio(SNR) than othermodels and the lowest RootMean-Square Error(RMSE),ENAEandEBiaswith respect to thex/y/zcoordinate time series.The results show that the EMD-Wavelet model has relative advantage in the data processing of GPS dynamic defor mation monitoring.

empiricalmode decomposition(EMD);wavelet transformation;noise reduction model;dynamic deformation;data processing

1671-5942(2010)05-0077-05

2010-03-10

地理空间信息工程国家测绘局重点实验室开放课题(200812)

赵玉玲,女,1976年生,讲师,硕士,研究方向为 GPS数据处理、变形监测研究.E-mail：zylqsq@163.com

P207

A