地形变旋转张量探讨＊

刘序俨 黄声明 林岩钊

(福建省地震局,福州 350003)

地形变旋转张量探讨＊

刘序俨 黄声明 林岩钊

(福建省地震局,福州 350003)

在分析地形变组成的基础上,指出旋转与应变张量矩阵同出而异名,两者皆为位移梯度矩阵的不同组合。旋转张量矩阵为位移梯度矩阵与其转置矩阵之差的 1/2,为一反对称矩阵,由于该矩阵的对角线元素为零,旋转张量矩阵已退化为一向量,该向量的方向与模表征了地壳的刚体旋转角位移。给出了位移梯度矩阵、旋转与应变张量矩阵的普适表达式,而旋转张量矩阵的诸元素皆为位移分量偏导数的减组合,要想根据旋转张量矩阵计算旋转角位移,必须首先求得位移分量的坐标函数式,且计算得到的旋转角位移又不是一直接观测量,为了克服求取位移分量坐标拟合式的困难,又能对地表旋转成分进行直接观测,提出了一种简单且行之有效的观测与计算方法。

地壳形变;位移梯度矩阵;旋转张量矩阵;旋转观测;计算方法

1 引言

对于前者,dr与 dr′之间关系可用下式表示:

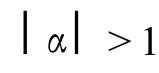
对于后者,显然式 (1)是不适用于图 2所示情况,此时须用一个地形变张量矩阵取而代之,对图 2中的情况[1,2]:

式中,F为地形变张量矩阵,对于二维平面情况,F为二阶矩阵,对于三维空间,F为 3阶矩阵,根据文献[1,2],任何一种地形变可由平移、旋转和应变 3部分组成,因此,式(2)中的地形变张量矩阵 F又可分解为：

式中,I为单位矩阵,表示刚体平移;Ω为旋转张量矩阵,表示刚体旋转;ε为应变张量矩阵,表示地块形状的改变。将式(3)代入式(2),则得表示地形变的普适表达式：

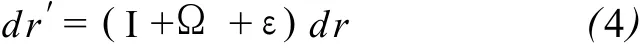
式(4)的几何含义就是如图 2的那样对 dr进行以下操作:先把 dr平移使其A与A′重合,然后把 dr旋转一个β角,使 dr与 dr′重合,最后使 dr伸缩,使 dr等于 dr′。同样,这种操作也适用于平面上的正方形和空间中的立方体,不过除了平移、旋转和伸缩外,正方形和立方体的相邻两直角边的夹角也可能发生改变,即剪应变。既然地形变是由平移、旋转和应变 3部分组成,宛如颜料中的红、黄、蓝 3种原色可以调出百色一样,平移、旋转与应变也是地壳变形的 3种“原色”,它们表征了地壳质点在外力激励下做出的响应。

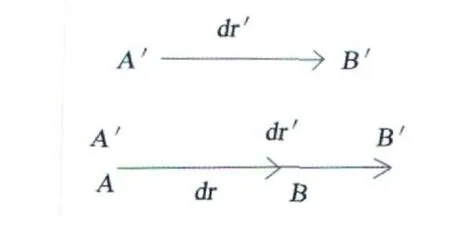
图1 平行情况Fig.1 Parallel case

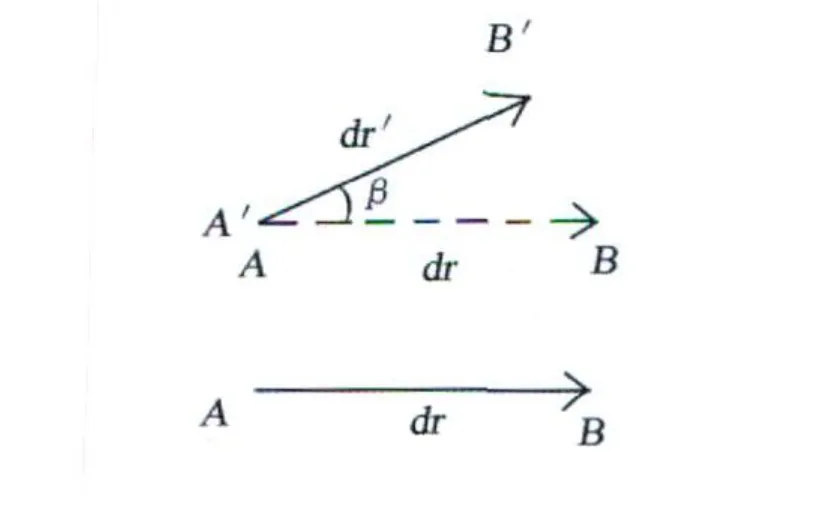
图2 不平行情况Fig.2 Unparallel case

旋转与应变皆由质点位移所引起,它们分别为位移梯度矩阵的不同组合,旋转与应变张量矩阵之和即等于位移梯度矩阵。设其质点位移向量为 u,E为位移梯度矩阵,则有：

2 位移梯度矩阵及其性质

设M与N为在ξ坐标系中相邻近的两点。在外力作用下,M移至M′,N移至 N′。M的位移为u(r),N的位移为 u(r+Δr),其中,Δr=(ΔS1,ΔS2, ΔS3)T为M点的位置向量的增量(图 3)。

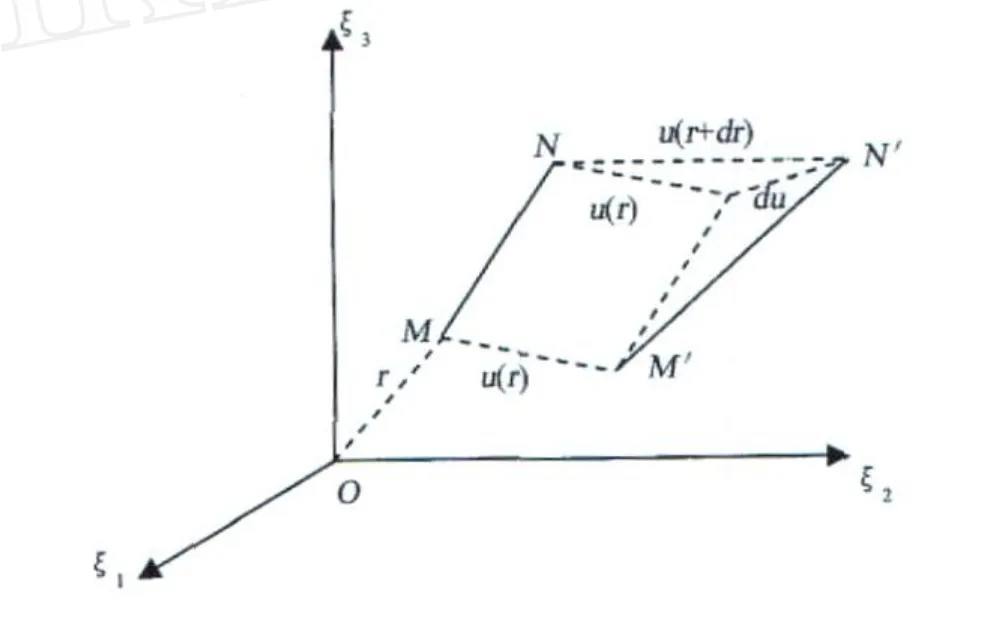
图3 地壳质点位移示意图Fig.3 Sketch of crustal particle displacement

在图 3中,由于M与 N是非常接近的两个点,对M点位移所引起的N点位移向量 u(r+dr)进行台劳级数展开,仅取一次项可得:

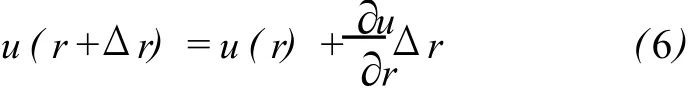
由上式又可得:

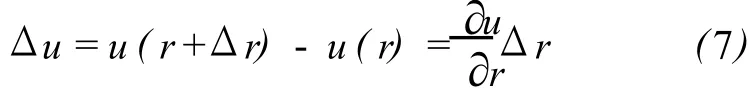
根据向量值函数导数定理[3],由式 (5)可得:

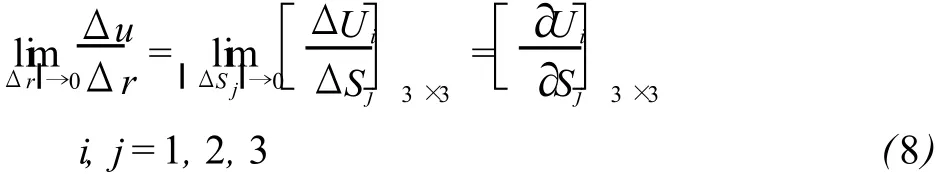
式中,ΔU1、ΔU2、ΔU3分别为位移向量 u的全微分在M点单位活动标架上的分量,则 E的表达式为：

E称为M点处的位移梯度矩阵或位移向量 u的雅可比矩阵。由张量理论,位移向量为一阶张量,位移梯度矩阵为二阶张量矩阵。

位移梯度矩阵 E给出了位移向量的空间变化率,刻画了地壳介质的形变。这种“形变”体现在介质内部质量体积元位移的相互作用上,这种介质内部相互作用产生的“形变”,在弹性力学中称为“应变”,位移的空间变化率即为应变[4]。

由M点的位移梯度矩阵 E及转置矩阵 ET所构成的两种特定组合,分别给出由M点位移在其邻域所产生的地壳介质的应变和旋转张量矩阵[1,2],前者可表达为:

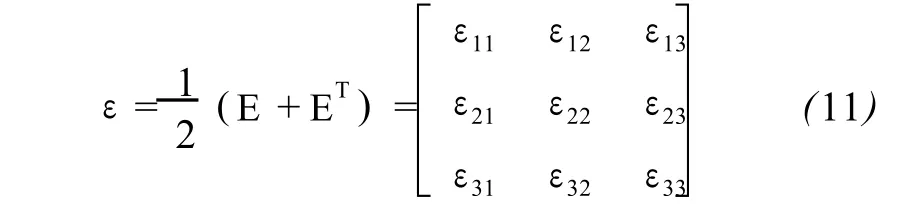
式中,

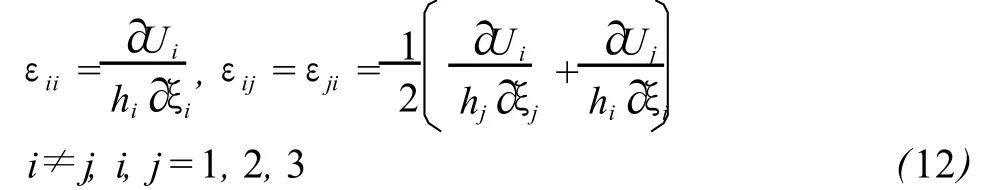
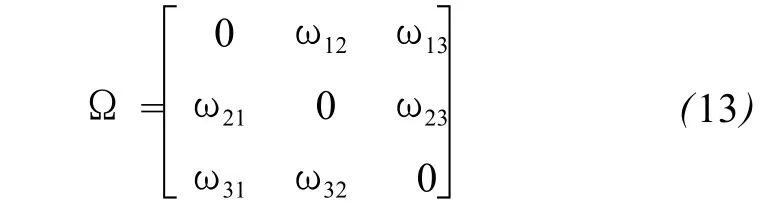
后者可表示为:

式中,

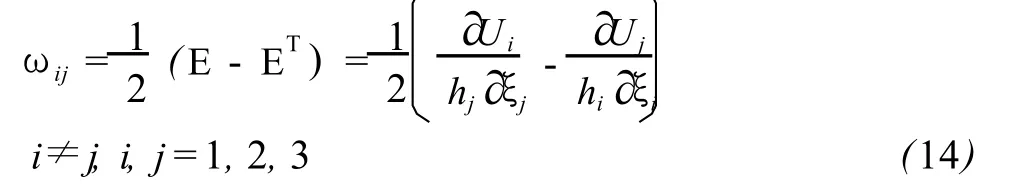
其中,

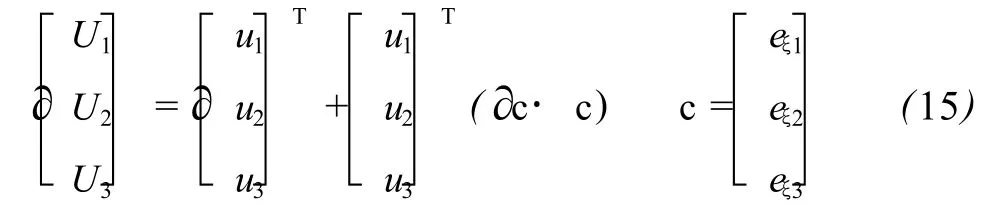
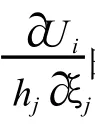
前者的对角线元素分别表示在M点处正交坐标架轴上的线应变,而非对角线诸元素则分别表示在M点处由彼此相互正交的坐标轴所构成的平面上的剪应变,在三维空间中,应变张量矩阵仅有 6个独立变量,在二维情况,仅有 3个独立变量。虽然在不同的正交曲线坐标系下应变张量矩阵的元素各不相同,但它们都是相似矩阵,都能刻画在M点处的所有地形变信息。无论由哪一种坐标系下的应变张量矩阵均能求出M点处的地形变不变量,这些不变量与坐标系的选择无关,这些不变量隐藏在该矩阵之中。它们分别为该质点处的主应变及其主方向,在由彼此正交的两个主方向构成的平面上的剪应变为零,主方向上的应变即为主应变,主应变之和等于该矩阵的迹,为该质点处的体应变,矩阵的行列式等于主应变的乘积,该矩阵皆可由主方向的单位向量所构成的变换矩阵转换为以主应变为对角线元素的对角矩阵,主应变与主方向皆可由矩阵的特征值方程求得,以上这些不变量正体现了应变张量矩阵的几何物理性质。对于后者,由于为一反对称矩阵,此时该矩阵已通化为一向量,该向量表征了该质点处的刚体旋转方向,而该向量的模则为刚体旋转的角位移。M点处的地形变应变与旋转成分是由M点处的位移空间形变率即位移梯度所产生的,因此M点处的应变与旋转则表征了位移梯度矩阵的性质。

3 旋转张量矩阵及其性质

从式 (13)可看出,旋转张量矩阵为反对称矩阵,因此式(13)中的对角线分量皆为零,此时,旋转张量已退化为一个旋转向量。式 (13)中各分量ωij(i≠j)表示为位移所引起的旋转向量的模在 ij平面上的分量,具有明确的几何意义。例如,ω12表示在M点处的单位标架中由 e1和 e2单位向量所构成的平面上(以下称为 12平面)所发生的角度转动量(以弧度为单位),在单位时间的转动量称为角速度。ω12值的正负由下述约定给出:如果ω12为正值,那么,根据右手法则,四指按反时针由 e1转向 e2,大拇指所指的方向就代表在 12平面上所发生的转动向量的方向[5],该转动的大小与方向可表示为ω12e3;反之,ω21代表在 12平面上按顺时针方向转动,转动向量的方向指向 -e3,该转动的大小和方向可表示为 -ω21e3,因ω21=-ω12,则ω21e3=-ω12e3,说明 12平面上的转动向量与约定的时针方向无关,其他两个平面上的旋转向量亦可依此类推。最后可得由式(13)所表示的旋转向量ω表达式为

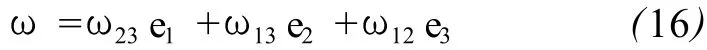
设:cosα、cosβ与 cosγ分别为向量ω的方向余弦,则ω的单位向量为

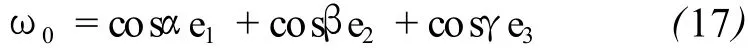
式中,

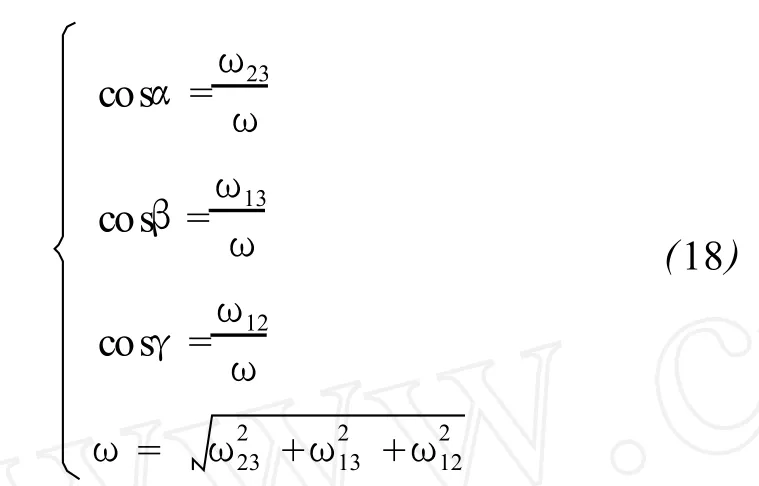
旋转向量ω又可表示为

式中：ω0表示由位移所引起的单位转动向量;ω表示由位移所引起的与ω0相正交平面上的旋转量,其正负根据右手法则给出;ω23、ω13、ω12分别为ω在23、13、12平面上的分量,而ω本身也就是旋转向量的模。

不同坐标系下的旋转张量矩阵亦如应变张量矩阵一样,也可通过这两个坐标系的转换矩阵 c进行转换,其表达式为[1]:

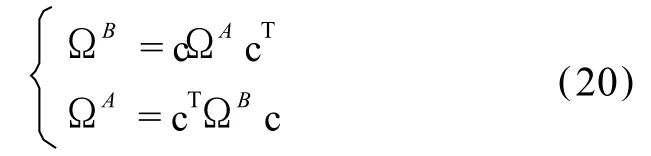
式中,c=cB,其中 cB与 cA分别为由M点处的直角坐标系的单位标架转换到该点处的 B与 A坐标系的单位标架的转换表达式[5],且 ccT=I,故旋转张量矩阵如同应变张量矩阵一样也是相似矩阵,旋转分量与的转换亦同应变张量分量的转换一样是可转换的。

考虑到旋转张量矩阵ω为一个由式 (13)所表示的一个已退化的转动向量,当然ω =(ω23,ω23, ω23)亦可由坐标系转换公式得到以下相互转换表达式:

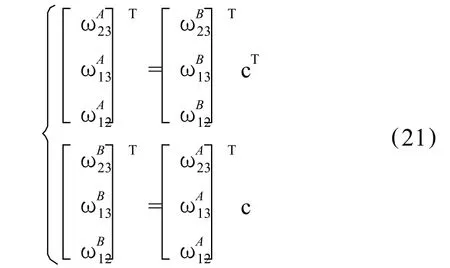
式中,c=cA由于 c为正交矩阵,ccT=I,不难证明：

故不同坐标系下的旋转张量都能给出该质点处地壳整体旋转方向及其旋转角位移,这正是该矩阵所隐藏的几何物理不变量。

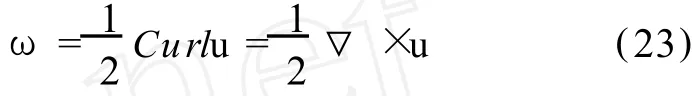
顾及到式 (15),则式 (23)又可写为：

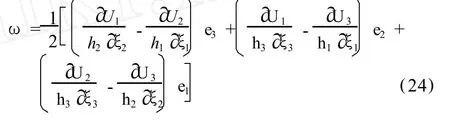
4 地表面旋转张量的运动方程

旋转张量矩阵与应变张量矩阵都是同出而异名,即它们都是位移梯度矩阵的不同组合。前者为减组合,后者为加组合。根据数字滤波理论,前者为高通滤波器,后者为低通滤波器。在无地震情况下,地壳噪声一般表现为地脉动,其振幅都是较小的,因此,地壳旋转分量的数值一般比平移和应变要小。

地壳旋转如同应变一样,都是由地壳剪切应力所引起的。在这里,我们仅讨论地表旋转问题,因为我们目前还没有这样一个三维形变观测系统。根据牛顿第二定律与物体转动的力矩平衡原理,绕垂直于地表面的 Z轴旋转的旋转运动方程为[4]:

式中,θz是绕 Z轴的转动角,Iz为地壳体积微元dxdydz绕 Z轴的转动惯量,Gz为体积力力矩密度的Z轴分量,Gzdxdydz为该 Z轴分量绕 Z轴的旋转力矩,Iz=ρdxdydz[(dx)2+(dy)2]平均,其中ρ为地壳密度,σxy与σyx分别为地表面上的 2个剪应力。当体积微元 dxdydz趋于零时,转动惯量 Iz趋于零的速度更快,因而上式变为:

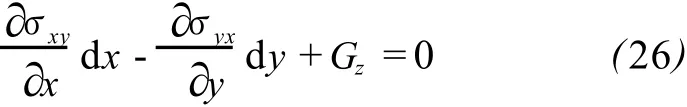
在小应力情况下,上式又可近似写成:

同理,可得绕 X轴与 Y轴转动的运动方程:

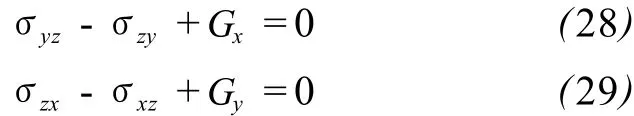
式中,Gx与 Gy分别为体积力力矩密度的 X轴与 Y轴分量绕 X轴与 Y轴的旋转力矩。

当上式 Gi(i=x,y,z)=0,则得到剪切应力张量的重要关系式:

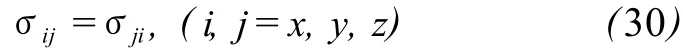
文献[7,8]则直接从力矩平衡方程出发,在假定Δxi(i=1,2,3)→0前提下,同样得到了σij=σji。式(30)表明剪切应力是对称的。在线性小应变弹性波传播理论中,Gi=0是允许的。应力张量的对称性“消隐”了转动运动方程存在的形式,因此,在一般文献中对转动运动方程都不予讨论[4]。张量的对称性本身就呈现了“旋转成分”。

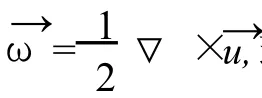
既然旋转为组成地形变 3种成分中的一种,为一种独立成分,据笔者所知,到目前为止,虽然还没有一种专门的观测系统对其进行观测研究,但旋转作为地形变的一种独立成分,如何对它进行观测一直成为学者关注的焦点,其中,地震旋转仪的研制与试测就是显著的一例[9]。该旋转仪的本体为一完全对称的圆环形旋转惯性摆。虽然该仪器经过 1年的试测记录到了一些地震旋转波,但因地震位移波与旋转波同时到达,位移波会对旋转波产生极强的干扰,使旋转波被淹没在位移波中难以分辨,如何抑制地震 P波波动使之不会对旋转波产生影响,是一项非常关键的而又十分不易解决的难题,终因种种原因遭遇到重重困难,最后也只好将试测样机束之高阁而作罢,但不管怎样,研制者却开创了中国地震旋转仪研制的先河。迄今为止,还没有找到一种行之有效的观测系统与计算方法,在这里,本文提出一种简单易行的观测方案与计算方法。

5 旋转张量计算面临的困境

在取得诸测站的位移观测资料后,是否就可直接按式(11)与(13)进行地应变与旋转形变分析呢?回答是否定的,其原因是我们无法知道位移的坐标函数表达式,因此也就无法得到位移诸分量对该测站坐标的偏导数值。根据弹性力学理论基础,地壳介质这种弹性体中所有的物理量都是连续的,即是说,密度、位移、应变、应力都被假定为空间点的连续变量,并且假定空间点变形前后应该是一一对应的,位移向量为空间点的单值函数并具有所需的各阶连续偏导数[1],在一般情况下,我们无法知道位移的坐标函数表达式,但天体起潮力引起的测站位移是个例外。根据固体潮理论,在采用古登堡-布伦地球模型的基础上,天体起潮力引起的位移可根据该测站处的天体起潮力计算出来,从而可得到天体起潮力所导致的测站位移在球坐标系下以测站地心向径ρ、地心纬度φ与经度λ为变量的位移坐标函数表达式,最后根据式(11)与(13)进行应变与旋转张量计算,以得到固体地球应变与旋转张量的理论值[10-12],把应变固体潮观测值进行维尼迪柯夫调和分析,就可在振幅与相位方面对两者进行分析,以取得可靠的地形变信息。

在一般不知位移坐标函数表达式的情况下,如何解决应变张量计算呢?为此,许多学者进行了探讨,例如,文献[13]建议以若干个观测点作为支撑点来确定某个内插函数,在进行内插时,如果没有给观测值提供一种假定的动力学模型数据的话,采用纯粹的几何模型内插方法必须满足观测点的分布密度能保证相邻观测点之间的线性内插达到足够的精度以满足研究的需要,以及所选定的几何内插函数能确保相邻观测点之间存在近似线性内插关系,内插函数可采用样条逼近技术或拟合推估方法求得。文献[14]认为,在我们所得到的是一些离散点的位移,而不是点位的函数时,则无法解析地求出偏导数,此时必须用数值估计,有两种方法可供采用。一种是求一个小区域的导数,此时需要采用有限元方法,另一种是求一个点上的导数,此时可用有限差分法。因此,利用应变张量矩阵公式计算应变张量遇到了建立位移分量的坐标线性拟合公式这个难题。在利用旋转张量矩阵公式计算旋转张量时也遇到了同样的难题,如何绕开这个难题,直接利用位移观测资料进行旋转张量计算只有另觅他途。

6 旋转观测与计算方法探讨

地壳旋转作为地形变的一种独立成分,除了文献[1,2]从理论上给予证明以外,更主要的是要以观测事实予以证明,因为自然科学不像思辨哲学那样仅是在形而上学层面上进行思考,而自然科学本身是一种实证科学,对任何一种理论都必须经过观测或实验加以验证。如何对地形变旋转成分进行观测,本文提出一种观测方案 (图 4)。图中OA与OB相互垂直,分别位于 x轴与 y轴上,OA=OB,分别在A、O、B进行位移观测。

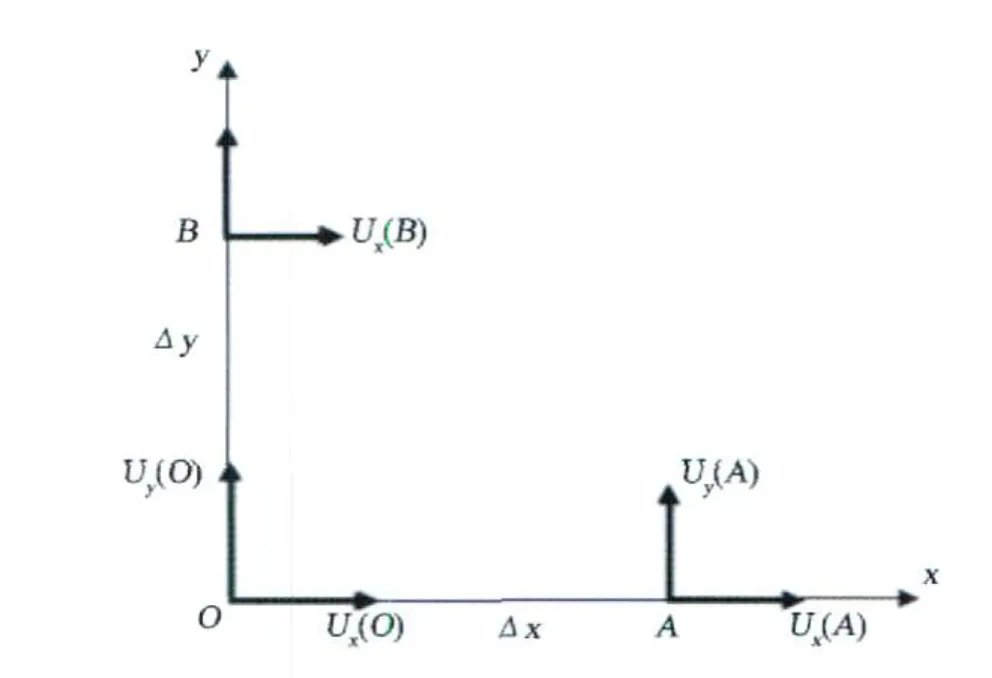
图4 旋转观测示意图Fig.4 Sketch of rotation observation

图 4中Ux(·)与 Uy(·)分别为 A、O、B点的位移分量,其中,Ux(O)与 Ux(A)的差异会使 OA发生胀缩,而Uy(O)与 Uy(A)的差异则会使 OA发生偏转,类似地Uy(O)与Uy(B)之差异会使OB胀缩, Ux(O)与Ux(B)会使 OB发生偏转。图中 OA边旋转角位移向量ωOA为:

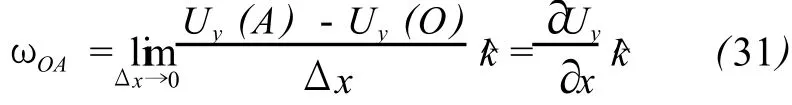
类似地,OB边的旋转角位移向量ωOB为:

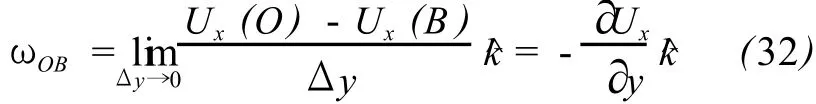
以上计算是依照右手法则来确定旋转向量方向的,旋转方向定为为与地表垂直向上方向的一个单位向量,如果式 (31)与 (32)中右边的系数为正,表明旋转为逆时针,反之为顺时针方向。最后,两边位移所引起的O点处的地壳旋转位移ω为上述两式之平均值：

上式正是由式 (14)所表示的二维地表应变张量矩阵中的ωyx的旋转向量表达式。

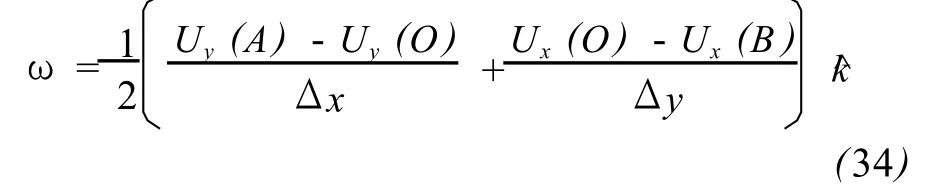
采取这样的方案不但可以对地表旋转进行观测,而且可以进行计算,从而可以弥补这方面的空白。

至于三维地壳旋转张量观测,我们必须在空间6个不同方向进行位移观测。目前,我们还不可能在地壳洞体中建立这样一个观测系统,因此,也就无法取得其他两个旋转张量。如何对地壳旋转进行完备观测与计算,仍然是一个今后值得重视的问题。

在这里,值得提出的是,本文给出的地形变旋转张量观测与计算公式(34),是受旋转张量式 (14)的启发,式(34)不过是式 (14)在图 4中等边直角三角形上的近似展开罢了,观测与计算原理是正确的。由于福建省地震局 GPS网点布设时,没有考虑地旋转观测方案,因此,无法以观测资料实例对该方法的可行性与实效性进行验证。不过我们可以对式(34)计算地旋转张量的精度进行估计。

设:Δx=Δy=l,设 GPS单点观测位移的中误差为σu,设σω为ω的计算中误差,根据误差传播定律,不难得出:

在目前 GPS单点观测精度最高可达σu=1 mm,设 l=100 m=105mm,则按式(35),此时,σω= 10-5(弧度)=2″,如取 l=1 000 m=106mm,则σω=0.2″,如 l=10 km=107mm,则σω=0.02″,此时ω的测定中误差相当于倾斜固体潮最大幅度。因此,采用此种方法是无法胜任旋转固体潮观测的,但可以满足对大震的同震旋转观测,此种旋转观测系统是可以对大震所引起的同震旋转作出响应的,因为大震的同震旋转量较大。

7 认识与讨论

文献[4]认为应力矩阵的对称性“消隐”了应力转动方程存在的形式,但不是意味着旋转成分的消失,而是认为应力张量的对称性本身就呈现了“旋转成分”,旋转成分的存在是一种客观事实,不过其量值比正应变与剪应变值要小罢了,大地震所造成的烟筒或铁轨扭曲就是旋转成分存在的一种例证。究其原因,旋转是由不同距离处的质点位移之差异所造成的,即是由质点的不同空间形变率所造成的。本文从地形变构成出发,阐述了应变与旋转张量矩阵皆为位移梯度矩阵的不同组合,并指出位移梯度矩阵刻画出了空间形变率,并给出了应变与旋转张量矩阵的普适表达式。由式(11)与 (13)可发现,要想根据位移观测资料进行应变与旋转张量分析,首先要给出位移分量的坐标函数式,除了应变固体潮外,我们一般是无法获知位移分量的坐标函数的表达式,此时要从建立动力学或几何模型并采用线性内插方法来取得位移分量的坐标拟合式,在此基础上,才能根据式(11)与(13)进行应变与旋转张量分析[10,11],从这个意义上说,根据式 (13)对位移分量的坐标拟合式取偏导而取得的旋转并不是一种直接观测量,而且存在拟合误差带来的影响。对此,本文给出了一种绕开式(13)进行旋转分析的方法,提出了一种在等边直角三角形 3个顶点进行位移观测及其计算方法,该方法简单易行,可避免采用式 (13)要确定位移分量坐标函数式的困难。在目前的地形变观测系统中,唯缺失旋转观测系统,只有建立了旋转观测系统,我们才真正具有了对地形变 3种成分进行观测的一个完备的观测系统。

1 王敏中,等.弹性力学教程[M].北京：北京大学出版社, 2002.(WangMinzhong,et al.The course of elastic mechanics[M].Beijing：BeijingUniversity Publishing house,2002)

2 米恩斯W D.应力与应变[M].丁中一译,王仁校.北京：科学出版社,1982.(Means W D.Stress and strain[M]. Springer-VerlayNew York,Inc,1976)

3 杨永发,徐勇.向量分析与场论[M].天津：南开大学出版社,2006.(Yang Yongfa and Xu Yong.Analysis of vector and field theory[M].Tianjin：Nankai University Press, 2006)

4 牛滨华,孙春岩.固体弹性介质与地震波传播[M].北京：地质出版社,2005.(Niu Binhua and Sun Chunyan.Solid elastic medium and seismic wave trans mit[M].Beijing：Geologic Press,2005)

5 刘序俨,等.正交曲线坐标系的应变张量转换[J].大地测量与地球动力学,2008,(2)：71-76.(Liu Xuyan,et al. Conversion of strain tensor matrices between t wo orthogonal curvilinear coordinates[J].Journal of Geodesy and Geodynamics,2008,(2)：71-76)

6 GreenbergM D.Advanced engineeringmathematics(The 2nd edition)[M].Beijing：Publishing House of Electronics Industry,2004.

7 Lay T,et al.Modern global seis mology[M].San Diego,New York：Boston：Academic press,1995.

8 Jaeger J C.Elasticity fracture and flow[M].Lodon：Methuen amp;CO.LTO.New york：John wi-leyamp;sows.inc,1964.

9 蔡乃成,付子忠.旋转地震仪的研制[J].地震学报,2009, 31(3)：347-352.(Cai Naicheng and Fu Zizhon.Manufacture of rotation seis mograph[J].Acta Seismological Sinica, 2009,31(3)：347-352)

10 北京大学地球物理系,等.重力与固体潮教程[M].北京：地震出版社,1982.(Depart ment of Geophysics of BeijingUnivisity,et al.Course of gravity and earth tide[M]. Beijing：Seis mological Press,1982)

11 梅尔基奥尔 P.行星地球的固体潮[M].杜品仁,等译.北京：科学出版社,1984.(Melchior P.The tides of the planet earth[M].Translated byDu Pinren,et al.Beijing：Science Press,1984)

12 Vanicek P and Krakiwsky E J.Geodesy：The concepts[M]. New York：Elsevier Science Publishing company,I NC. 1986.

13 Altiner Y.Analytical surface deformation theory for detection of the earth’s crust movement[M].Berlin.Heidelberg.etc.Springer-Verlag,1999.

14 瓦尼切克 P.四维大地测量定位[M].黄立人,等译,陈鑫连校.北京：地震出版社,1990.(Vanicek P.Four-dimensional geodetic positioning[M].Springer International 1987)

RESEARCH ON ROTATION TENSOR OF CRUSTAL DEFORMATION

Liu Xuyan,Huang Shengming and Lin Yanzhao
(Earthquake Adm inistration of Fujian Provine,Fuhzou 350003)

On the basis of the analysis of component combination of crustal deformation,it is pointed out that strain and rotation tensor matries both are different combination of displacement gradient matrix,and the rotation tensormatrix is a half of diffrence of both displacement gradieutmatrix and it is transpose one and anti-symmetrix one.Because its diagonal elements of rotation tensormatrix is zero so it turns into a kind of vector in degradation, the direction and modulus of the vector characterize the crustal rigid rotation.

crustal deformation;displacement gradieatmatrix;rotation tensormatix;rotation observation;calculation of rotation

1671-5942(2010)05-0057-07

2010-06-21

中国地震局老专家基金

刘序俨,男,1939年,研究员,长期从事固体潮与地壳形变研究.E-mail：xuyanliu@126.com

P315.72+5

A