大型国际综合性运动会奖牌数预测研究
——以北京奥运会为例
2010-11-06王国凡薛二剑唐学峰
王国凡,薛二剑,唐学峰
大型国际综合性运动会奖牌数预测研究
——以北京奥运会为例
王国凡1,薛二剑2,唐学峰3
基于计量经济学理论,依据人口数、人均GDP、主场优势、社会制度、上届奥运会的成绩,利用多元非线性回归分析建立初步模型;考虑世界各国竞技体育实力存在差距,利用模糊C均值聚类分析理论,将竞技体育实力划分为5个等级,通过引入虚拟变量,提出经济学与竞技体育实力差异理论相结合的改进模型,对2008年北京奥运会奖牌数进行预测分析。结果表明,该模型既能揭示世界各国奥运会奖牌数变化的总体趋势,又能克服竞技体育实力差异对预测精度的影响;适用于大型国际综合性运动会奖牌数的预测,具有较强的科学性和可行性。
计量经济学;大型国际综合性运动会;奥运会;奖牌;预测模型
自二战后,社会学家和经济学家从不同的国家性质与经济水平等因素分析影响国家在奥运会中获得的奖牌数。较早关于这方面的研究成果有Ball[1],Grimes A Ray等人[2]和Levine N[3],而近30年后关于这方面的理论研究才重新被人们所关注[4-8]。Johnson Daniel K N和Ayfer Ali[9]通过引用一国人均收入(以人均GDP为依据)、人口数、政治体系(是否为一党专政君主政体,是否为社会主义国家或是资本主义国家)、地理位置与气候,以及是否为主办国等社会、经济学方面因素作为变量,基于经济学方法与这些变量,他们甚至计算出一个国家要派出一名运动员参加奥运会及每赢得一枚奥运奖牌需要的“投资费用”。Bernard与Busse[4]以此为基础,提出了基于计量经济学理论,将人口数和经济资源(以GDP为依据)作为生产要素,利用柯布—道格拉斯生产函数对奖牌数分部进行了研究。此外,Bernard和Busse还引入主场优势、不同国家经济体系(计划经济和市场经济)的虚拟变量,同时添加了上届奥运会奖牌数这一变量,并建立回归预测模型,使预测结果更加准确。
在2008年奥运会奖牌预测方法中,国内学者运用了时间序列法[10]、趋势直线外推法[11]、统计回归方法[12]、概率模型[13]、灰色预测[14-15]等方法和手段,开展了大量研究。吴殿廷,吴颖[15]利用模型与东道主效应(或称主场优势)相结合预测出2008年北京奥运会中美两国可能会有的奖牌数,取得了很好的预测结果。但是,这些预测方法仅以历届奥运会奖牌数为基础,部分文献虽结合了主场优势进行分析预测,但这类“以牌推牌”的预测方法,存在较大的偶然性。国外也有不少专家对2008年北京奥运会奖牌数进行了预测研究,遗憾的是,大部分预测结果与真实成绩都存在着较大差距。
笔者认为,单纯运用经济学原理提出预测的模型可能适合一个或若干个国家,但把它应用到所有国家是缺乏依据的。本文以2008年北京奥运奖牌数的预测研究为例,尝试提出一种适用于大型国际综合性运动会奖牌数的较精确模型。在笔者建立的新模型中,不仅考虑到国家人口数、人均GDP、主场优势、上届奥运会成绩这些关于社会、经济学方面的变量,另外,加入了在国际竞技体育中关键的实力差距评估这一因素。事实上,正是这些因素的共同作用决定了一个国家可能获得奖牌的数目[16-17]。新模型引用模糊C均值聚类分析理论,将各国竞技体育实力划分为5个等级,通过虚拟变量,基于计量经济学与各国竞技体育实力差距相结合的方法,对2008年北京奥运会成绩进行预测研究,结果发现该模型预测精度大大提高。该模型也适用于国际综合大型运动会奖牌数的预测。
1 数据来源
本文采用的世界各国在历届奥运会获得奖牌数据来源于中国奥委会官方网站上公布的成绩。世界各国人口数据来源于Angus Maddison,Historical Statistics for the World Economy:1-2003 AD。世界各国GDP来源于联合国贸易与发展组织统计的数据。2008年世界各国GDP来源于由美国中央情报局(CIA)在The World Factbook《世界概况》刊登统计的数据。本文计算所用世界各国人口数及GDP均为举办历届奥运会年底的数据。
2 模型的依据
2.1 人 口
人口数对参赛国获得奖牌的多少起着重要的作用。人口基数大,国家具有潜在运动天赋的运动员数目就大,就有更大几率出现优秀运动员从而获得奥运奖牌。
2.2 人均GDP
国家的经济发展水平可通过国内生产总值(GDP)与人口比值来表示,即人均GDP。人均GDP对一个国家的体育发展起着至关重要的作用,对获得奥运会奖牌数具有重要的制约作用。
2.3 主场优势
在奥运会比赛中,主场优势往往起着十分重要的作用[18-20]。由于主办国的运动员更加熟悉比赛环境和竞赛器材,同时,众多本国观众的主场助威会调动本国运动员的积极情绪和裁判无意识的支持主队等,最终能够在一定程度上有助于主办国运动员竞赛成绩的提高。
2.4 社会制度
社会制度的不同对奥运会也会产生影响。社会主义国家对待像夏季奥运会这样的大型国际竞赛,在经济上往往通过“举国体制”来进行全力保障;而资本主义的经济体制是自由市场经济,其投入也是有条件的。有研究表明,不同国家的经济体制,对奥运会奖牌是有影响的——社会主义国家比资本主义国家在奥运会奖牌分享中,更具有优势。
3 初步模型的建立与分析
3.1 建立初步模型
基于上面的因素分析,将影响国家获得奥运会奖牌数目的因素选择为人口、人均GDP、主场优势、社会制度以及上届奥运会成绩,从而建立如下计量经济模型:
以奖牌占有率M作为因变量[4],即:

上式表示第i个国家在当届奥运会取得的奖牌数(medalsi)与当届奥运会总奖牌数(的比值。根据本文前面的分析,若不考虑边际收益递减原理,人口越多,就会拥有更多有天赋的优秀运动员;人均GDP越大,就会有更多经费训练出优秀的运动员,从而共同决定着国家在奥运会比赛中取得的成绩,笔者在此将它们的影响程度以非线性的方式进行处理,取人口数(log(POP))与人均GDP(log(POP))以10为底的对数作为变量,建立的多元非线性回归模型如下:

式中:M为奖牌占有率;t为时间趋势(1=1988年奥动会,2=1992年奥动会);POP为当年参赛国人口数(个);PGDP为当年参赛国人均GDP(美元);Home为虚拟变量,Home=1表示奥运会主办国,Home=0表示非主办国;P为虚拟变量,P=1为社会主义国家,P=0为资本主义国家;α为常数;βj,(j=1,…,5)为各解释变量的系数。
3.2 基于多元非线性回归模型的2008年北京奥运会成绩预测
二战以后,越来越多的国家与地区代表队陆续参与奥运会同台竞技;而在这之前,由于部分国家受多种原因限制无法参加夏季奥运会以及大国之间的抵制,因此,受到社会经济方面的影响因素也较小,使得各国运动成绩缺乏可比性。此外,在1984年洛杉矶奥运会中,以前苏联为首的社会主义国家抵制参与奥运会,导致世界各国奖牌占有率失衡,即1984年奖牌占有率可视为异常数据。因此,为了提高预测精度,1988年汉城奥运会不作为预测样本数据,最终选取1992—2004年奥运会数据进行预测。在国家选择上,将获得至少一枚奖牌的国家作为当年奥运会的样本国家,而没有获得奖牌数的国家被剔除。
基于1992—2004年数据的拟合,即可得到模型(2)各解释变量的系数,并假设解释变量系数在对2008年北京奥运会的预测中是不变的;与此同时,可类似建立金牌占有率(Mg)多元非线性回归模型。得到的奖牌与金牌占有率回归结果见表1。

表1 1992—2004年奖牌与金牌占有率回归结果
根据该回归结果,预测出2008年北京奥运会奖牌数与金牌数(见表2、表3)。从表2、表3的预测结果可以看出,部分国家的预测奖牌数、金牌数与真实值差距较大。
针对上述传统多元非线性回归模型在预测精度上的不足,笔者引入模糊C均值聚类算法,对奥运会参赛国竞技体育实力进行等级评估;在此基础上,利用引入多个虚拟变量表示竞技体育实力等级,对模型(2)进行改进,提出一种更高预测精度的预测模型。

表2 2008年北京奥运会各国奖牌预测值
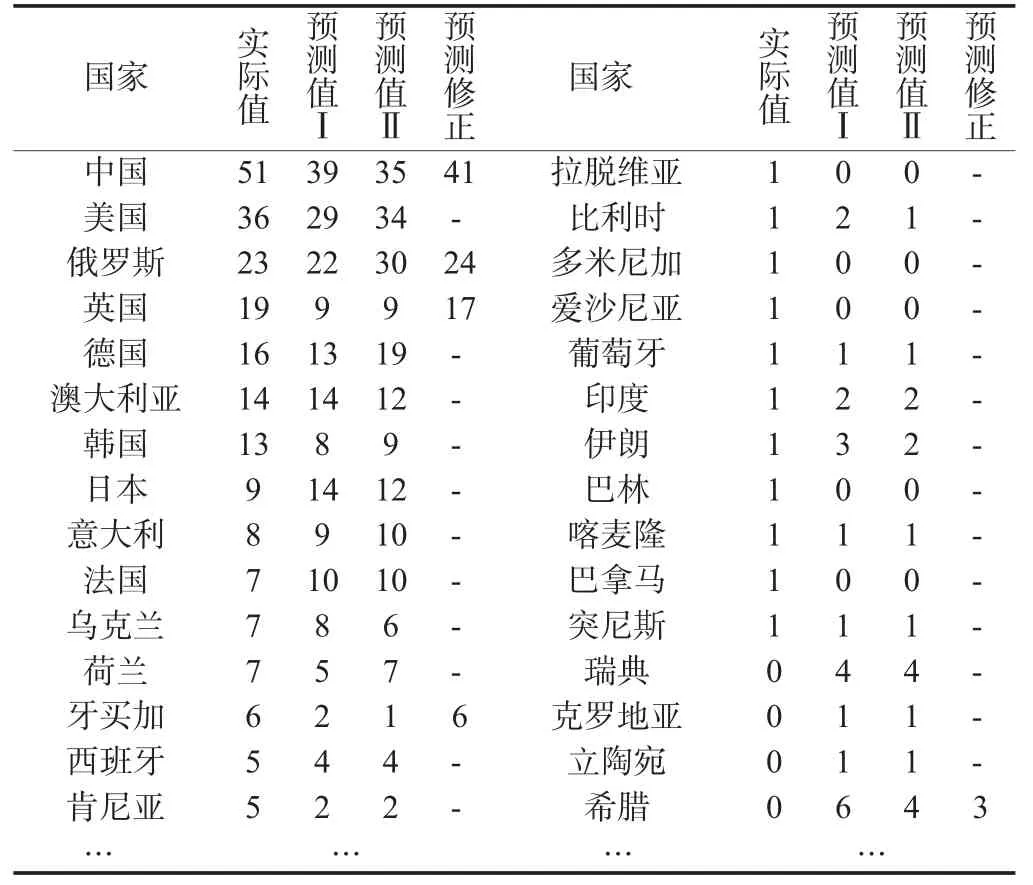
表3 2008年北京奥运会各国金牌预测值
4 基于模糊C均值聚类算法对参赛国进行等级评估
在模糊C均值(FCM)聚类算法中,每一个数据点按照一定的模糊隶属度隶属于某一聚类中心,这一聚类技术作为对传统聚类技术的改进,是jim Bezdek于1981年提出的。该方法首先随机选取若干聚类中心,所有数据点都被赋予对聚类中心一定的模糊隶属度,然后通过迭代方法不断修正聚类中心,迭代过程以极小化所有数据点到各个聚类中心的距离及隶属度值的加权和优化目标[21-22]。
首先对奥运会参赛国建立5个评价等级(见表4),依据1988至2004年各国参加奥运会获得的金牌、银牌、铜牌以及奖牌总数为样本数据,统计出这5届奥运会世界各国获得的奖牌总数,利用模糊C均值聚类进行分类比较,实现工具为MATLAB软件。MATLAB模糊逻辑工具箱提供了模糊C均值聚类方法即FCM命令函数[23]。得到的分类结果见表5。
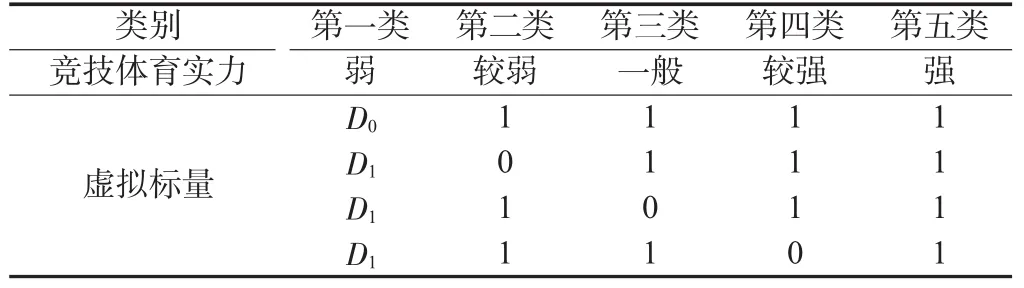
表4 参赛国竞技体育实力标度的划分及虚拟变量设定

表5 基于模糊C均值聚类分类结果
5 改进的多元非线性回归预测模型
在奥运会奖牌数预测中,许多经济变量是可以定量度量的;而某些影响因素若无法量化,将对模型预测结果存在着很大的影响。如竞技体育实力是反映各国家比赛成绩的核心要素,也是决定获得奖牌数增多或减少的主要因素,竞技体育实力将直接决定谁将成为奥运会的霸主。因此,建立的经验模型要想取得准确的预测值,就必须考虑竞技体育实力的影响。笔者采用虚拟变量方法,将这一定性因素定量化,建立含有多个虚拟变量的回归模型,从而能够更好地反映出影响因素的共同作用。
5.1 含有多个虚拟变量的多元非线性回归模型的建立
在当代计量经济学分析中,利用模型进行回归分析是应用比较广泛的一种数据分析技术。一般回归分析中的变量都是定量变量,这是因为模拟回归需要样本数据。而在实际中,模型仅考虑定量变量是不够的,如果某一变量确实受到定性因素影响,将虚拟变量技术用到回归模型中就可以解决该问题[24],本文中就利用了虚拟变量将主场优势影响因素定量化。
将奥运会参赛国进行分类后,所有参赛国竞技体育实力划分为5个不同的等级,可利用虚拟变量表示这5个等级(见表2),再将虚拟变量添加到多元非线性回归模型从而建立新模型。为了避免“虚拟变量陷阱”[25],利用4个虚拟变量D1,D2,D3,D4分别表示5个类别,即:


从表1的回归结果可知,社会制度虚拟变量系数很小,换句话说,在现在奥运会比赛中,社会主义国家的几乎不占优势。故将其忽略。
新模型为:
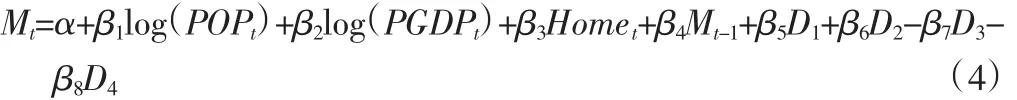
利用1992—2004年奥运会实际数据为样本数据,对新模型(3)进行回归,得到的结果见表6。
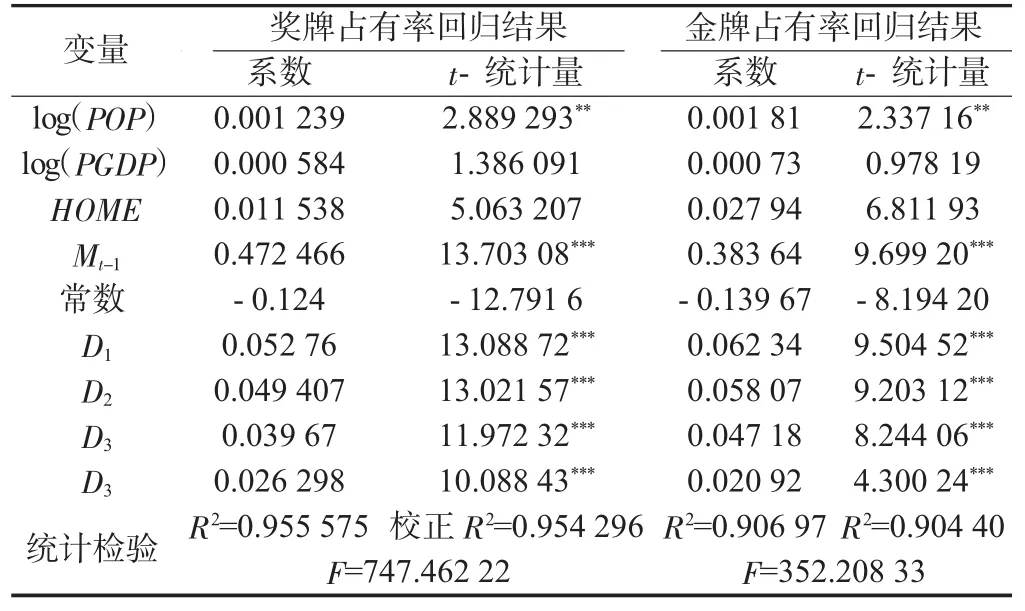
表6 改进模型的奖牌与金牌占有率回归结果
从回归结果可以看出,利用模糊C均值聚类对参赛国分类后,通过添加虚拟变量得到的改进模型(3),拟合优度R2明显大于模型(2)。因此,改进的新模型(3)预测结果更好,因为,R2值越高,预测越准[26]。
5.2 新模型对2008年北京奥运会成绩预测结果
有了新模型(3),就可以重新对2008年北京奥运会奖牌数进行预测,预测结果数据见表2、表3。从预测中可以看出,基于模糊C均值聚类分类的改进模型,在对大部分国家的奖牌预测中,其精度都要高于前模型。
5.3 竞技体育实力“等级跳跃”
利用模型(3)对中国、俄罗斯、德国等几个国家进行预测,结果存有较大差距。出现这种情况是有原因的,在这里可称之为国家的竞技体育实力“等级跳跃”现象;笔者认为:竞技体育实力“等级跳跃”,是指若将奥运会参赛国分成若干个等级区间,各国分别处于不同的等级,但在奥运会比赛中,有时会出现个别国家运动员发挥异常出色,夺牌的实力明显变强,从而使得该国的竞技实力等级上升一级甚至多级;相反,有的国家运动员集体发挥不理想,从而会使该国的竞技实力等级下滑的现象。事实上,历届奥运会都出现过竞技体育实力“等级跳跃”现象。以此分类,中国的竞技体育实力为“较强”,但曾在1988年汉城奥运会出现过实力等级下滑的现象,当届中国的竞技体育实力等级就下降为“一般”。
俄罗斯在近两届奥运会的实力与中国相当,尤其是在夺金上能够体现出来。2000年奥运会俄罗斯比中国多获4枚金牌,但在2004年奥运会上,中国超出俄罗斯5枚金牌。将俄罗斯在2008年奥运会的竞技体育实力下降一个等级(即为类别4),那么奖牌数与金牌数预测值(见表2、表3中的“预测修正”)与真实值相当接近。牙买加异军突起在2008年北京奥运会的田径赛场,搅乱了奥运会田径赛场的原有形势。这个非洲小国的田径实力紧随美国、俄罗斯,因此,使得预测值与真实值差距较大。如果将牙买加的竞技体育实力等级提升,那么预测的奖牌数与真实值差距较小,金牌数预测与真实值则完全相同(见表2、表3中的“预测修正”)。此外,从2008年奥运会还可以看出,英国、乌克兰发挥出色,等级提升;德国、日本、荷兰、罗马尼、匈亚利等国发挥失常,等级下降。但从总体来看,大部分国家均处于所分类的等级之中。
另外,在奥运会主办国,有时还会出现一个“主场优势跳跃”现象,即主办国不仅占有主场优势,甚至还可以由于多种有利因素而再次提升一个甚至多个等级。针对这种情况,笔者利用基于模糊C均值聚类改进的非线性多元回归模型对1992—2004主办国通过“主场优势跳跃”进行预测,即不仅考虑主场优势这个虚拟变量,同时,将主办国体育竞技实力提升一个或多个等级,所计算得到的预测值与真实值相差无几。对于2008年北京奥运会的主办国中国,上升一个等级(即为类别5)再进行预测,从而得到的奖牌数为97(见表2、表3中的“预测修正”),与实际奖牌数仅差3枚。
值得一提的是,主办国通常在下届奥运会表现出实力有较大幅度的下滑现象,笔者称之为“次场效应”。例如,文中对希腊的预测结果,真实值与预测值就存在着较大的差距。从分类结果可以看出,希腊竞技体育实力等级为“较弱”,若将希腊下降一个等级,即为类别1(弱),其预测值与真实值则较为接近。
6结 论
(1)从计量经济学角度出发,指出人口数、人均GDP决定着国家获得奥运会奖牌数目,同时分析了主场优势以及上届奥运会成绩也会对获得奖牌数有一定程度的影响。以此为依据,建立初步的多元非线性回归模型(2),这样建立的模型,解决了以往国内仅以历届奥运会成绩为基础,部分结合了主场优势所提出的预测结果偶然性较大的问题。
(2)提出了对世界各国竞技体育实力5个等级划分的理论。运用计量经济学与竞技体育实力等级差异理论相结合,对原有模型进行改进后建立的新模型(3)大大提升了对奥运会奖牌预测的精度。
(3)对于奥运会主办国奖牌数的准确预测,有时还应该考虑引入“主场优势跳跃”因素。
(4)对奥运会主办国在下届奥运会比赛中奖牌数的准确预测,有时还应该考虑引入“次场效应”因素。
7 分析与讨论
7.1 等级跳跃
新模型(3)的建立虽然提升了以往预测的精度,但还存在对少数国家预测不准确的问题,笔者在此引入了竞技体育实力“等级跳跃”现象。以竞技体育“等级跳跃”为判据,进行了预测修正,从而提升了预测的准确性。笔者认为,出现竞技体育实力“等级跳跃”现象的原因,可能是由于某国个别运动员异常出色的发挥;或者是某国在特定时期对竞技体育给予相当大的重视及特别加大竞技体育的投入等,这些有利因素都能使国家体育竞技实力等级上升;相反,一个国家若在自己的强势项目中发挥失常,或者国家政治不稳定,甚至处于战乱状态等,这些不利因素都会使其体育竞技实力等级下滑。
在预测结果中,我们发现竞技体育实力“等级跳跃”现象出现的概率很小,在对2008年北京奥运会奖牌预测中有10个国家出现“等级跳跃”现象,在金牌预测中仅有3个。
7.2 主场优势跳跃
在北京奥运会中,中国代表团取得了骄人的成绩,笔者认为:其中“主场优势跳跃”带来的效益不可忽视。产生的原因除了由于主办国的运动员熟悉比赛环境和竞赛器材、众多本国观众的主场助威、运动员情绪兴奋和裁判无意识的支持主队外,我国政府对北京奥运会极度重视,采用“举国体制”加大对体育的投入和启动“119工程”等。正是这些因素的综合作用,在2008年奥运会中我国运动员的总体实力大大上升,出现了“主场优势跳跃”现象。
7.3 次场效应
笔者在研究中发现,主办国在下届奥运会中表现出的实力通常会有较大幅度下滑:即竞技体育实力等级不但会从“主场优势”回归到正常等级,而且还可能会从正常等级再下滑一个甚至多个等级,笔者称之为“次场效应”。之所以会出现“次场效应”,可能为参赛国的重视不够、投入相对较少、参赛国运动员由于前一次比赛成绩过好,而出现了无意识的松懈现象等,这也是我国运动员对于将要参加的2012年伦敦奥运会所要注意和克服的问题。
[1]Ball Donald W.Olympic Games Competition:Structural Correlates of NationalSuccess[J].International Journal of Comparative Sociologu,1972,12:86-200.
[2]Grimes A Ray,WilliamJ.Kelly,Paul H,Rubin.A Socioeconomic Model of National Olympic Performance[J].Social Science Quarterly,1974,55,777-782.
[3]Levine Ned.Why Do Countries Win Olympic Medals?Some Structural Correlates of Olympic Games Success:1972 [J].Sociology and Social Research,1974,58:353-360.
[4]Bernard Andrew B,Meghan R Busse.Who Wins the Olympic Games:Economic Resources and Medals Totals[J].Review of Economics and Statistics,2004,86(1):413-417.
[5]Kuper G,E Sterken.Olympic Participation and Performance since 1986[J]. Mineo.Department of Economics,University of Groningen.2001.
[6]Oyebanke Oyeyinka.The Determinants of Participation and Success at Olympic Games:A Cross-Country Analysis [J].CarrollRound Proceedings,2007,2:156-180.
[7]Bian Xun.Predicting Olympic Medal Counts:The Effects of Economic Development on Olympic Performance [J].The Park Place Economist,2005,VIII,37-44.
[8]Condon,E M,Golden B L,Wasil E A.Predicting the success of nations at the Summer Olympics usingneural networks[J].Computer&Operations Research,1999,26,1 243-1 265.
[9]Johnson Daniel K N,Ayfer Ali.A Tale of Two Seasons:Participation and Medal Counts at the Summer and Winter Olympic Games[J].Social Science Quarterly,2004,85(4):974-993.
[10]蔺银萍,王建军.运用时间序列法预测2008年奥运会奖牌数[J].南京体育学院学报,2007,6(1):31-32.
[11]范珣,齐辉.运用趋势直线外推法预测2008年奥运会中国获奖牌数[J].辽宁体育科技,2007,29(4):57-58.
[12]江立平.用统计回归方法预测我国代表团在2008年奥运会上的奖牌数[J].南京体育学院学报,2007,6(2):54-55.
[13]刘万民,吴瑕.基于概率模型对2008北京奥运会中国代表团成绩的预测[J].湖北师范学院学报,2008,28(1):16-19.
[14]姜一鹏.第28届奥运会中国奖牌预测[J].天津体育学院学报,2004,19(2):86-87.
[15]吴殿廷,吴颖.2008北京奥运会中国金牌赶超美国的可能性——基于东道主效应的分析和预测[J].统计研究,2008,25(3):60-64.
[16]古扎拉蒂.林少宫,译.计量经济学[M].林少宫,译.北京:中国人民大学出版社,2000.
[17]白海波,郭权.我国与奥运强国竞技体育实力的比较研究[J].沈阳体育学院学报,2004,23(2):163-117.
[18]N J Balmer,A M Nevill,A M.Williams.Modelling home advantage in the Summer Olympic Games[J].Journal of Sports Sciences,2003,21:469-478.
[19]刘万民,柳建庆.体育比赛中主场优势的研究[J].中国体育科技,2006,42(3):101-105.
[20]田雷,刘万民,刘丹.夏季奥运会比赛主场优势的量化研究[J].中国体育科技,2008,44(1):3-6.
[21]高新波.模糊聚类分析及其应用[M].西安:西安电子科技大学出版社,2004.
[22]钱同惠,沈其聪,葛晓滨,等.模糊逻辑及其工程应用[M].北京:电子工业出版社,2001.
[23]张曙红,孙建勋,诸克军.基于遗传优化的采样模糊C均值聚类算法[J].系统工程理论与实践,2004,24(5):121-125.
[24]闻新,周露.MATLAB模糊逻辑工具箱的分析与应用[M].北京:科学出版社,2001.
[25]赵家敏,彭虹.我国证劵投资基金羊群行为及其对股价影响爱那个的实证研究[J].系统工程,2004,22(7):38-43.
[26]严忠,岳朝龙,刘竹林.计量经济学[M].合肥:中国科学技术大学出版社,2005.
Prediction of the Number of Medals in International General Games:With Beijing Olympic Games as an Example
WANG Guofan1,XUE Erjian2,TANG Xuefeng3
(1.School of PE,Anhui Normal University,Wuhu 241000,China;2.School of Mathematics and Computer Science,Anhui Normal University,Wuhu 241000,China;3.School of Physics,University of Science and Technology of China,Hefei 230026,China)
Based on theories of econometrics,population,GDP per capita,home advantage,social system,achievements in the previous Olympic Games,this paper established a preliminary model with multiple non-linear regression analysis.Considering the discrepancy in competitive sports strength between countries,the authors divided competitive sports strength into five scales with fuzzy C-means clustering algorithm.By introducing dummy variable,the authors proposed a revised model which combines theories of economics and discrepancy in competitive sports strength,and conducts a prediction analysis of the number of medals in 2008 Beijing Olympic Games.Results showed that this model can reveal the general tendency in the change of Olympic medals won by different countries,and can overcome the influence of discrepancy in competitive sports strength on prediction precision.This model can be applied to the prediction of the number of medals in international general games due to its scientificity and feasibility.
econometrics;international general game;Olympic Games;medal;prediction model
G 80-32
A
1005-0000(2010)01-0086-05
2009-09-03;
2009-11-15;录用日期:2009-11-16
国家体育总局体育文化发展中心项目(项目编号:08TYWH146);安徽省哲学社会科学规划项目(项目编号:AHSK07-08D102)
王国凡(1964-),男,安徽肥西人,安徽师范大学副教授。
1.安徽师范大学体育学院,芜湖241000;2.安徽师范大学数学计算机科学学院,芜湖241000;3.中国科学技术大学近代物理系,合肥230026。
