长输管道排水过程中的气阻现象与气阻定律
2010-11-04安金龙
安金龙
(中国石化集团江汉石油管理局油田建设工程公司,湖北潜江433123)
长输管道排水过程中的气阻现象与气阻定律
安金龙
(中国石化集团江汉石油管理局油田建设工程公司,湖北潜江433123)
长输管道在试压排水过程中时常会发生气阻现象,导致排水压力大大高于理论估算值。工程实践中,应该采取措施防止气阻现象的产生,以减小试压排水的困难。文章运用流体力学的基本理论,结合塑料管水力实验和长输管道工程实践,对气阻现象进行了分析,对所谓“气阻定律”做出了否定的辨析。文章的结论对于长输管道工程的试压排水和输配水系统的正常操作具有一定的指导意义。
长输管道;水压试验;排水;水力实验;气阻定律
1 长输管道排水压力的估算
建设中的长输管道一般都采用洁净水作为分段试压的介质。分段试压合格后,用压缩空气推动清管球(器)排出管内的试压水。
根据流体力学的基本原理,排水清管器在管内正常行走的正面压力(压缩空气压力,在此称为排水压力)Pe至少应大于以下5种阻力之和:试压管段的最低点与排水口的静水压差γw·ΔHi;试压管段的沿程水头损失γw·hf;试压管段的局部水头损失γw·hj;推动清管器正常行走所需的压力(用于克服清管器的重力与摩擦阻力)Pg;排水口的压力(背压)P0。也就是说,一般情况下应有:

式中Pe——排水清管器正常行走的排水压力(表压,下同)/MPa;
γw——水的重度,取0.01 MN/m3;
ΔHi——试压管段最低点与排水口的高程差/m;
hf——设定排水速度下的沿程水头损失/m;
hj——设定排水速度下的局部水头损失/m;
Pg——推动清管器正常行走所需的压力/MPa,一般为0.2~0.3 MPa;
P0——排水口压力(背压)/MPa,一般为大气压力,取0.1 MPa。
在工程实践中,为便于应用,(1)式常常被简化成下式:

式中k——保险系数,一般取1.3~1.5;
ΔHm——试压管段沿线的最大高程差/m。一般情况下,运用(2)式计算出的排水压力与工程实际压力能够很好地吻合。根据计算结果确定的设备参数能够满足排水的操作要求。但有时也会发生异常现象:排水压力远远超过了按(2)式计算的Pe,排水清管器(球)还是不能正常行走,管内的试压水也不能正常排出。此时,我们通常认为产生了气阻现象。
那么,气阻现象为什么会产生?如何评估气阻现象对试压排水产生的影响?怎样防止气阻现象的产生?
对于这些问题,很多人进行了有益的探索,提出了自己的见解,其中包括翁友彬、阮天恩(以下简称翁—阮)的水力实验和他们的“气阻定律”。
2 气阻定律
翁—阮设计了一组长达17 m的管道实验装置,委托清华大学进行了相应的水力实验,试图揭示重力流输配水管道中发生的气阻现象,并合作撰写了一篇题为《气阻定律》的论文(http://www.studa.net/designs/060307/11483816.html)。
在这篇论文中,翁—阮通过考察管内微段空气柱的受力状态,推导出“气阻定律”:

式中PEmax——管道系统内E-E断面的最大压力(绝对压力);
Pa——管道系统出口处压力(绝对压力);
e——自然对数的底,e=2.718 28……;
σ——管道内气体的黏滞系数,与管道特性有关,通过实验测定;
lσ——管道系统内当量空气柱的长度;
D——管道内径。
对于这个“气阻定律”,笔者认为不能成立,理由是:
第一,它的基本假设与流体在管道内的实际运动状态相去甚远。翁—阮在推导“气阻定律”时将微段空气柱作为考察对象,建立了一个X轴方向的力学平衡式:
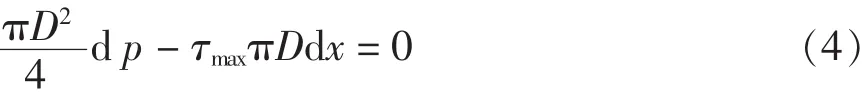
式中dp——微段空气柱的压降;
τmax——单位面积管壁对微段空气柱的黏滞阻力;
dx——微段空气柱的长度。
这个力学平衡式的成立至少需要两个基本条件:一是考察的对象为均质、连续的圆柱形刚性体;二是外部的约束为均质、连续、与圆柱形刚性体紧密接触的弹性体。而空气(或其他流体)本身一不连续,二不是刚性,且因其具有黏性、流动性和可压缩性,管道断面上各质点沿X轴方向的流速并不相同(一般沿半径方向从里到外逐渐减小)。也就是说,管道内的微段空气柱并不是平行向前移动。因此,式(4)的力学平衡式不能成立,由此而得出的“气阻定律”当然也不能成立。
第二,对水力实验的理论解释不正确。翁—阮对自行设计的管道实验装置在实验中出现的断流现象进行了分析。他们认为,出现断流现象的原因在于管道系统的某一断面存在未知力PE,这个未知力阻止了水管中水的流动。同时,对一个确定的输水管道系统而言,存在一个临界掺气量,当输水管道系统内的掺气量达到或超过这一临界掺气量时,正常的水流被气体阻隔,发生断流。
笔者不清楚他们的实验装置能否清晰地观察到管内流体的运动状态,但通过类似的塑料管水力实验可以肯定地认为,这种分析既没有找到断流现象发生的真正原因,也没有注意到这套实验装置所阐释的普遍意义。只要我们注意到这套实验装置所具备的“管道系统存在波状起伏”和“管道系统内同时存在气、液两相介质”这两个基本特性,就可以用传统流体力学的基本原理加以分析和解释(参见本文第3部分)。管道系统产生气阻现象的基本条件就是要具备这两个基本特性。出现断流现象是系统作用的结果,而不是某一断面未知力作用的结果。
第三,气阻定律不具备基本的普遍适应性。根据翁—阮的“气阻定律”,当管道直径D、特性值σ和出水端压力Pa一定时,PEmax随着管内当量空气柱长度lσ成指数上升。也就是说,如果翁—阮“气阻定律”的基本假设是正确的,对于如图1所示的最简单的输水管道系统,要想出水口有水流出,应该有he>>h0;但实际上,如果忽略管道的沿程和局部水头损失,只要he>h0,打开阀门n、o,管道内就会有介质流动,出口端就会有水流出。这种现象符合传统流体力学的基本原理。

图1 简单重力输水系统示意
3 塑料管水力实验
尽管翁—阮的“气阻定律”不能成立,但他们在论文中阐述的断流现象(实际上就是通常所说的气阻现象)确实是客观存在。那么,到底是什么原因导致实验装置产生了断流现象呢?
为了更直观地反映这类管道系统内气、水两相介质的运动状态,笔者用透明塑料管进行了类似的水力实验。方法如下:
在标有高程刻度的墙壁上将一根长10 m、直径20 mm的透明塑料管安装成不规则的蛇形状态(见图2)。蛇形管的一端与大气连通,另一端与高位水箱相接。打开阀门n、o,在水流速度足够小、水流到达末端o或保持流动时,将形成如图2所示的状态:在k-j、g-f、c-b段会残存一定体积的空气。
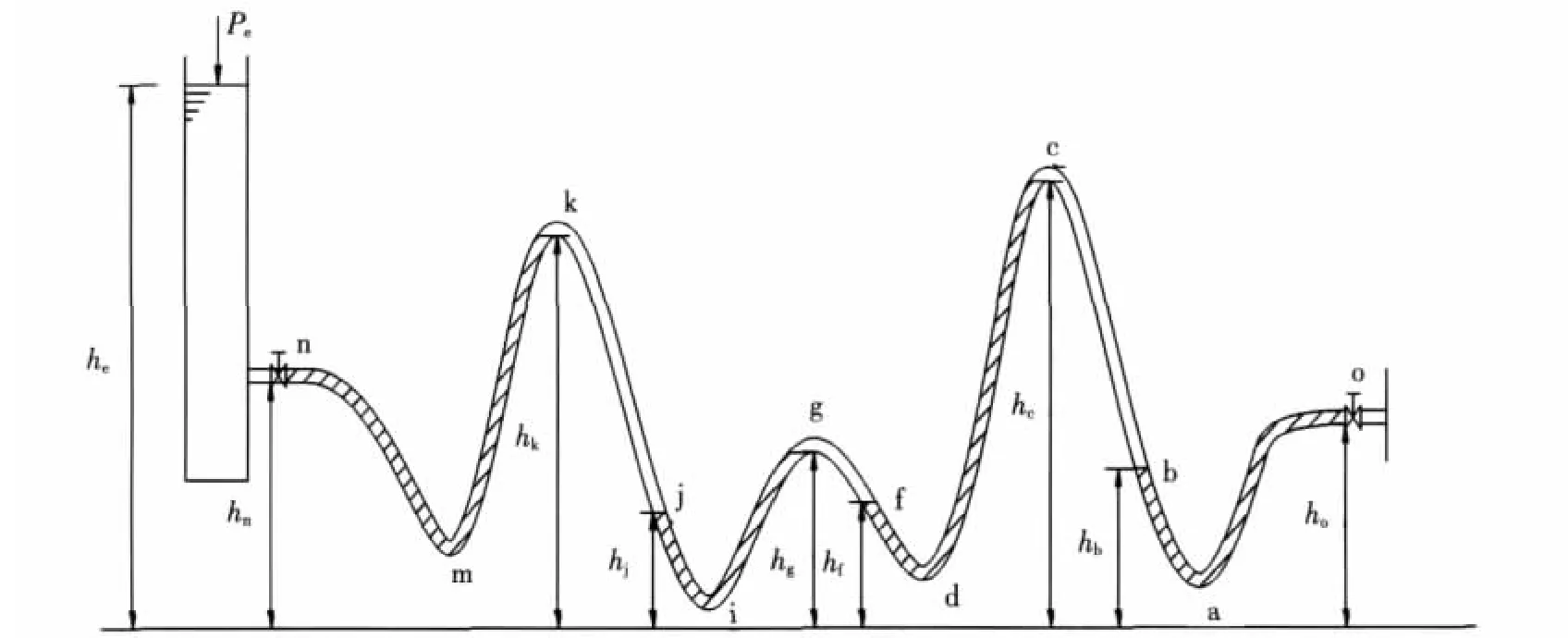
图2 塑料管水力实验示意
设出水端压力为Po,进水端压力为Pe,忽略空气的质量,在管道系统达到静态平衡时有:
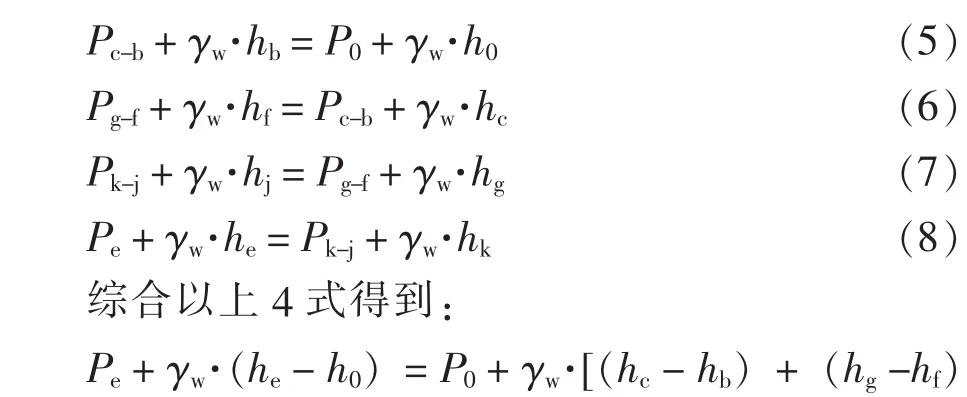

从(9)式可以看出,对于波状起伏,且存在气—液两相介质的管道系统而言,管道系统内液体正常流动的基本条件是:进水端液面的压力与位能之和大于出水端液面压力、位能与各段弯管波峰两侧液柱的重力差之和。
对于翁—阮设计的水力实验装置(见图3),也可以用此方法进行分析。

图3 翁—阮水力实验装置(图中标高尺寸为m)
无论是先打开管道末端阀门,还是先打开管道首端阀门,如果不在水与空气之间放置隔离球(器),由于水与空气存在较大的密度差,在放水过程中,管道系统内总会或多或少地残存部分空气,从而形成一定的气阻。气阻的大小与管道系统的特性(波峰的高度、数量,管道的直径、内壁粗糙度等)有关。
极端的情况,下坡段(波峰右侧)的空气全部积存在管内,被上坡段(波峰左侧)的水密封住,此时系统末端出水所需的压力(排水压力)达到最大。这个最大的排水压力在具体情况下可以计算出来,但计算的过程非常复杂。我们通过(2)和(9)两式可以推断。

式中ΔH——管段波峰与波谷的高程差/m。
4 工程实践
某段蜿蜒穿行于低山丘陵地区的输气管道,管径711 mm,长度38 km,最大高程差72 m。管道焊接下沟后按要求进行了清管、测径,然后用洁净水作为分段试压的介质。试压合格后用板式清管器推球排水。按(2)式的计算,压缩空气的压力只要达到1.2~1.5 MPa就足以推动排水清管器将管内试压水推出。但实际操作中,进气端压力(表压)达到1.6 MPa,出水端的压力仍然为零,没有试压水排出。再加压至2.5 MPa,试压水仍不能排出。为什么会出现这种状况呢?
最初的分析只考虑到两种可能:一是测径完毕后,管道受外力作用(例如重型车辆或机械挤压)局部变形,致使排水清管器在某处卡阻;二是排水清管器损坏。
通过对管道沿线进行反复勘察,排除了第一种可能。将该管段从中间较高点切断后分段排水,推出排水清管器检查,发现清管器也完好无损,且断点一侧的管段没有试压水。
这说明在推球排水的过程中,发生了气阻现象。正是气阻的存在导致了排水清管器不能正常行走,试压水不能正常排出。
5 结论
通过以上的分析,并以工程实践为佐证,可以作出以下结论:
(1) 以理想流体为基本假设的传统流体力学的正确性不应受到怀疑。
(2) 翁—阮的“气阻定律”不能成立。因为它的基本假设与流体在管道内的实际运动状态相去甚远,对水力实验的理论解释不正确,且不具备基本的普遍适用性。
(3) 产生气阻现象必须同时存在两个基本条件:一是管道系统存在波状起伏;二是管道系统内同时存在气、液两相介质。
(4) 长输管道试压排水过程中发生气阻现象的主要危害是提高了排水压力,对排水设备提出了更高的要求。当排水设备无法达到这种要求时,可能导致切管。
(5) 在工程实践中,特别是在山区、丘陵地段长输管道的试压上水过程中,应该采取严密措施防止气阻现象的发生。一要合理使用隔离球(器),避免大量空气残存在管内;二要认真检查上水系统的密封状况,避免试压水中混入空气。
(6) 试压排水所需的最小压力不仅与试压管段的最大高差有关,也与试压管段的起伏状况(起伏次数和每次起伏的高差等)和试压水中的空气含量有关。基于这种考虑,(2)式中的k值应提高至2~2.5,并尽可能取上限,或者直接按(10)式估算排水压力。
Abstract:Air lock phenomena often happen during dewatering in long-distance pipeline pressure tests,which causes the dewatering pressure to be greater than the theoretical estimated value.In engineering practice,measures of preventing air lock phenomenon should be taken to reduce dewatering difficulty in pressure test.In this paper,air lock phenomenon is analyzed by applying the fundamental theory of fluid mechanics together with the plastic tube hydraulic experiment and the long-distance pipeline engineering practice,and the so-called“air lock law”is discriminated as a mistake.The conclusion offers certain guidance for dewatering in long-distance pipeline pressure test and the normal operation of water supply and distribution system.
Key words:long-distance pipeline;hydraulic pressure test;pipeline system;dewatering;hydraulic experiment;air lock law
(13)Air Lock Phenomenon and Law during Long-distance Pipeline Dewatering
AN Jin-long(Oilfield Construction Co.,SINOPEC Jianghan Petroleum Administration,Qianjiang 433123,China)
TE973.6
A
1001-2206(2010)05-0013-04
安金龙(1963-),男,湖北黄梅人,教授级高级工程师,1983年毕业于西南石油学院石油储运专业,2004年毕业于华中科技大学工程管理专业,获硕士学位。现从事施工技术管理工作。
2009-11-16
