特征多项式与最小多项式相等的充要条件及其应用
2010-11-02谭玉明
谭玉明
(滁州学院 数学系,安徽 滁州239012)
特征多项式与最小多项式相等的充要条件及其应用
谭玉明
(滁州学院 数学系,安徽 滁州239012)
给出了矩阵的特征多项式与最小多项式相等的几个充分必要条件以及它们的应用.
特征多项式;最小多项式;不变因子;初等因子
0 引言
设Mn(F)是数域F上n阶方阵的集合,F[x]是F上一元多项式的集合,A∈Mn(F)的特征多项式和最小多项式分别为fA(x),mA(x).设g(x)=xn+a1xn-1+…+a0∈F[x],则称n阶方阵
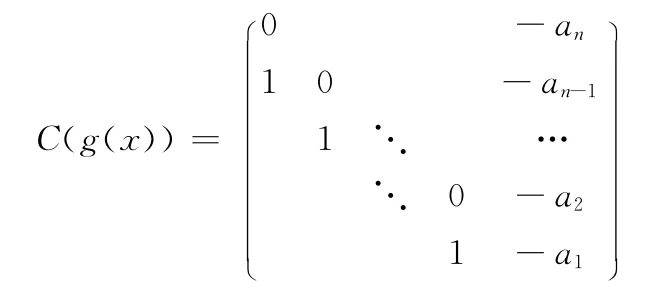
为g(x)的友阵.若首1多项式g1(x),…,gr(x)∈F[x],gi+1(x)|gi(x),i=1,2,…,r-1,则称准对角阵diag(C(g1(x)),…,C(gr(x)))为有理标准形.设p(x)为F[x]中首1不可约多项式,则称分块下三角形矩阵
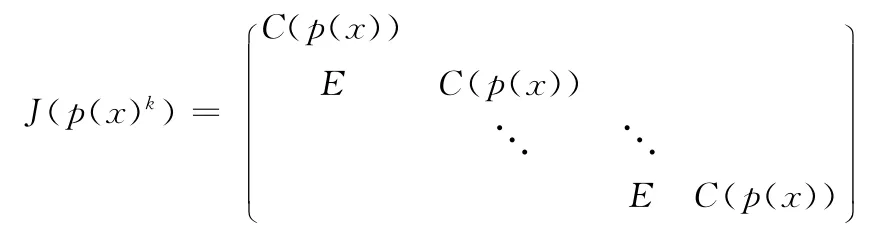
为(p(x))k的广义若当块,其中
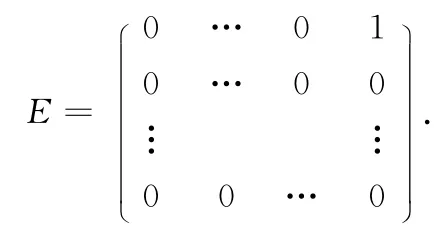
特别地,当p(x)=x-c时,
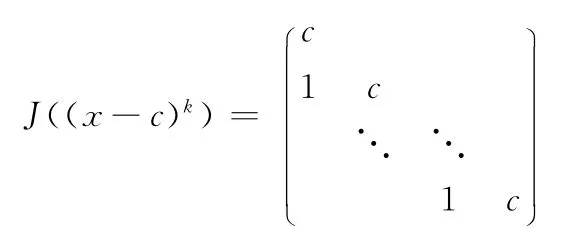
为k阶若当块,此时J((x-c)k)可简记为Jk(c).若p1(x),…,pr(x)是数域F上首1不可约多项式,则称准对角阵
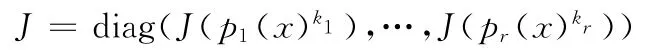
为广义若当标准形.特别地,当p1(x)=x-c1,…,pr(x)=x-cr时,J=diag(Jk1(c1),…,Jkr(cr))为若当标准形.不难验证,友阵、广义若当块、若当块的最小多项式与特征多项式均相等.若A∈Mn(F)在F上的不变因子组和初等因子组分别为g1(x),…,gr(x)(gi+1(x)|gi(x),i=1,2,…,r-1)和p1(x)k1,…,ps(x)ks(p1(x),…,pr(x)是F上首1不可约多项式),则A在F上相似于有理标准形diag(C(g1(x)),…,C(gr(x)))和广义若当标准形diag(J(p1(x)k1),…,J(ps(x)ks)),而且除了对角块的排列次序外两种标准形都是惟一的.
一般地,对A∈Mn(F),有mA(x)|fA(x)且两者根集相等,但实际问题中常遇到mA(x),fA(x)是否相等的问题,弄清这些问题有利于学生理解线性代数中的一些重要定理,因而对此作深入探讨是有意义的.
1 主要定理
定理1 设A∈Mn(F),则以下命题等价:
(1)mA(x)=fA(x);
(2)A的不变因子组为1,…,1,fA(x);
(3)A的有理标准形为C(fA(x));
(4)A对应的线性变换所作用的线性空间是一循环空间;
(5)A的初等因子组是F上两两互素的首1不可约多项式的幂:p1(x)k1,…,ps(x)ks;
(6)A的广义若当标准形为diag(J(p1(x)k1),…,J(ps(x)ks)),其中p1(x)k1,…,ps(x)ks是A在F上的初等因子组;
(7)在复数域C上,A的若当标准形为diag(J(c1),…,J(cs)),其中c1,…,cr为A的全部不同特征值;
(8)在复数域C上,A属于每个特征值只有1个线性无关特征向量;
(9)矩阵方程AX=XA的解空间的维数是n;
(10)与A可换的矩阵均为A的多项式.
易证(1)、(2)、(3)、(4)等价,(2)、(5)、(6)、(7)、(8)等价.为证(7)与(9)、(10)等价,先证明以下引理
引理1 设A=diag(J(c1),…,J(cs))为若当标准形,则矩阵方程AX=XA的解是X=(Xij)s×s与A的分法相同的分块矩阵,且

其中下三角分层矩阵是指如下形状的矩阵:
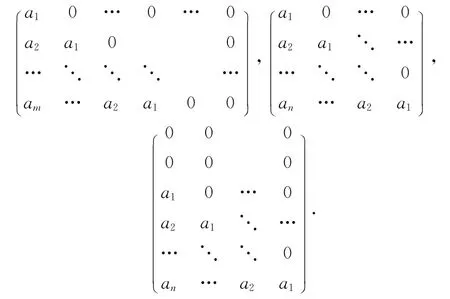
证明 方程AX=XA相当于J(ci)Xij=XijJ(cj),i,j=1,2,…,s.当ci≠cj时,J(ci)与J(cj)无公共特征值,故Xij=0.当ci=cj时,J(ci)Xij=XijJ(cj)相当于J(0)Xij=XijJ(0),两边乘开比较元素可得Xij为下三角分层矩阵.
下面证(7)与(9)等价:若在复数域C上A的若当标准形为J=diag(J(c1),…,J(cs)),其中c1,…,cr互不相同.设X是任意与A可换的矩阵且J=P-1AP,令Y=P-1XP,则方程AX=XA等价于方程JY=YJ,由引理1得Y=(Yij)s×s,其中

由于当1≤i≠j≤s时,ci≠cj,故Yij=0,从而Y=diag(Y11,…,Yss)且对角线上的小块均为下三角分层矩阵.所以Y中共有n个自由参数,故X=PYP-1中也有n个自由参数,所以方程AX=XA的解空间的维数是n.
若在复数域C上,A的若当标准形J=diag(J(c1),…,J(cs))中c1,…,cr有相同的情形,不妨设c1=c2,由引理1知,方程JY=YJ的解Y=(Yij)s×s中除对角线上的小块均为下三角分层矩阵外,Y12,Y21也是下三角分层矩阵.因此Y中自由参数个数大于n,从而原方程的解空间维数大于n.
再证(7)与(10)等价:若在复数域C上A的若当标准形为J=diag(J(c1),…,J(cs)),其中c1,…,cr互不相同.设X是任意与A可换的矩阵,J=P-1AP,Y=P-1XP,故JY=YJ.由上面证明知,Y=diag(Y11,…,Yss)且对角线上的小块均为下三角分层矩阵.取Lagrange-Sylvester内插多项式p(x),可使p(J)=Y.p(x)的具体算法参见文献[1].所以X=PYP-1=Pp(J)P-1=p(PJP-1)=p(A).
若在复数域C上,A的若当标准形J=diag(J(c1),…,J(cs))中c1,…,cr有相同的情形,X,Y同上所设,由上面证明知Y=(Yij)可以取到非准对角形Y0,所以不存在任何多项式p(x)使p(J)=Y0,从而也不存在任何多项式g(x)使g(A)=X0=PY0P-1.
注1 由(4)知,mA(x)=fA(x)等价于A有一个循环向量,即存在列向量α∈Fn,使α,Aα,…,An-1α为Fn的一组基.
由(7)知,mA(x)=fA(x)等价于A的若当标准形中属于每个特征值的若当块只有一块,可见这样矩阵的若当标准形中的若当块没有“分裂”.
由(10)知当且仅当mA(x)=fA(x)时,A的中心化子C(A)={X∈Mn(C)|AX=XA}等于{g(A)|g(x)∈C[x]}.
2 应用举例
推论1 设c1,…,cr为A∈Mn(F)的互不相同特征值,g(x)∈F[x],若g(c1),…,g(cr)互不相同且g′(c1),…,g′(cr)均不为0,则

证明 (⇒)由(7)可设A=Pdiag(J(c1),…,J(cr))P-1,其中c1,…,cr为A的全部不同特征值.则
g(A)=Pdiag(g(J(c1)),…,g(J(cr)))P-1,
其中

因g′(c1),…,g′(cr)均不为0,则g(J(ci))的若当标准形为

又由于g(c1),…,g(cr)互不相同,所以g(A)的若当标准形中属于不同特征值的若当块只有一块,由(7)得
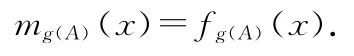
(⇐)假如mA(x)≠fA(x),由(7)知,A的若当标准形中属于某一特征值的若当块至少有两块,从而g(A)的也是.再由(7)得mg(A)(x)≠fg(A)(x).
注2 尽管A的若当标准形中属同一特征值若当块只有一个,但是g(A)的若当标准形中的同一特征值的若当块一般会发生两种情况的变化:一是原来属于不同特征值的几个若当块“整合”成了属于同一特征值的若干若当块,这是由于g(x)将这些不同特征值变为相同;二是属于某特征值ci的阶数大于1的若当块“分裂”成几个属于同一特征值的若当块,这是由于g′(x)将ci变为0.推论1的条件g(c1),…,g(cr)互不相同保证了A的属于不同特征值若当块不会“整合”,条件g′(c1),…,g′(cr)均不为0保证了A的属于同一特征值的若当块不会“分裂”.
推论1 容易推广到g(x)为在A的谱影上有定义的任意复变函数,谱影的定义可见文献[1],这里不再赘述.例如,当可逆矩阵A满足mA(x)=fA(x)时,mA3(x)=fA3(x),meA(x)=feA(x),mA-1(x)=fA-1(x),mA*(x)=fA*(x),但是mA2(x),fA2(x)不一定相等.
推论2 设A∈Mn(F)且mA(x)=fA(x),则A在数域F上可对角化当且仅当A在F中有n个不同特征值.
证明:(必要性)因A在数域F上可对角化,则A在数域F中有n个特征值.假如有相同的特征值,则mA(x)≠fA(x).充分性显然.
由此不难推出,对复数域上正规矩阵A,mA(x)=fA(x)当且仅当fA(x)无重根.故实对称矩阵A的特征多项式如有重根,则mA(x)≠fA(x).
推论3 设A∈Mn(F)在数域F上有k次方根B,即Bk=A.若mA(x)=fA(x),则mB(x)=fB(x).
证明 (反证法)若mB(x)≠fB(x),由(7)知,B的若当标准形中属于某一特征值的若当块至少有两块,则A=Bk的也是,矛盾.
注3 对实数域R上的矩阵A=Pdiag(Jk1(c1),…,Jkr(cr))P-1,若c1,…,cr∈R互不相同且A在R上有平方根B,则B的若当标准形为diag(Jk1(d1),…,Jkr(dr)),其中d1,…,dr∈R互不相同且d2i=ci,i=1,…,r.因此,当c1,…,cr出现0或负数时,A在R上没有平方根B.
下面以参考文献[2]、[3]中几个习题为例来说明定理1及其推论的应用.
例1 证明:σ2有循环向量,则σ也有循环向量.反过来对吗?
证明 化为矩阵问题是:A2有循环向量,则A也有循环向量.因A2有循环向量,由(4)知,则mA2(x)=fA2(x),再由推论3得mA(x)=fA(x),再由(4)知A也有循环向量.
例2 设σ是F上n维线性空间V的线性变换,有循环向量.证明:与σ可换的线性变换τ必为σ的多项式.
证明 化为矩阵问题是:A有循环向量,则与A可换的线性变换B必为A的多项式.这可直接由命题(4)(10)得.
例3 设σ是F上n维线性空间V的线性变换,证明:V中有向量α具有如下性质:对任意多项式f(x),若f(σ)α=0则f(σ)=0(此种向量称为分离向量).再证明,若σ有循环向量,则循环向量是分离向量.
证明 仍化为矩阵问题.设σ对应的矩阵是A,由A的有理标准形知,Fn中存在向量α以mA(x)为其最小零化子,由题意知对任意多项式f(x),若f(x)是α的零化子,则mA(x)|f(x),故f(A)=0,从而f(σ)=0.
若A有循环向量β,则由(4)知,mA(x)=fA(x),且β的最小零化子mA(x)=fA(x).对任意多项式f(x),若f(A)β=0,则mA(x)|f(x),从而f(A)=0,故β是分离向量.
例4 设N为域F上n阶方阵,Nn=0,Nn-1≠0.证明:不存在n阶方阵A使A2=N.
证明 由题意知mN(x)=fN(x)=xn,n>1.由(7)知N的若当标准形为n阶方阵Jn(0),由注3知N无平方根.
例5 设A为n阶复方阵,证明:存在一个n维向量α使α,Aα,…,An-1α线性无关的充分必要条件是,A的每个特征值恰有一个线性无关的特征向量.
证明 存在一个n维向量α,使α,Aα,…,An-1α线性无关,等价于Cn为一循环空间(对A),由(4)(8)等价直接可得证.
[1]王耕禄,史荣昌.矩阵理论[M].北京:国防工业出版社,1988.
[2]张贤科,许甫华.高等代数学[M].北京:清华大学出版社,1998.
[3]王品超.高等代数新方法[M].济南:山东教育出版社,1989.
On Necessary and Sufficient Conditions for Equality of Characteristic Polynomial with Minimum Polynomial and their Application
Tan Yuming
(Department of Mathematics,Chuzhou University,Chuzhou 239012,China)
Some necessary and sufficient conditions for equality of characteristic polynomial with minimum polynomial and their application are given in this paper.
characteristic polynomial;minimum polynomial;invariant factors;elementary factors
O151
:A
:1673-1794(2010)05-0001-03
谭玉明(1965-),男,副教授,硕士,主要从事代数学教学科研。
安徽省高等学校应用数学省级教学团队项目,滁州学院本科优质课程建设项目
2010-08-03
