用“几何画板”的函数功能研究物理疑难问题
2010-10-30何征宇
何征宇
(武进高级中学 江苏常州 213161)
“几何画板”在物理教学中的应用已经得到了广大物理教师的认可;它不仅能演示现象,还能够拓展思维空间,发现“意料之外,道理之中”的问题.
笔者在高三复习教学中碰到这样一道题:
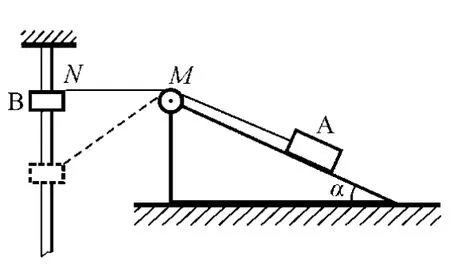
图1
如图1所示,一轻绳通过无摩擦的定滑轮,一端与放在倾角为α=30°的光滑斜面上的质量为m1的物体A相连,另一端与套在光滑竖直杆上质量为m2的物体B相连,定滑轮M到竖直杆的距离为l=m,杆上N点与定滑轮的高度相同,当物体B在距N点下方1m处时,A和B恰好静止.求:
(1)物体A和B的质量之比.
(2)将物体B从N点静止开始释放,物体B下滑过程中的最大速度大小.
分析:对于第(1)问,根据平衡条件不难求出,物体A和B的质量之比为m1:m2=4∶1.
对于第(2)问学生在讨论中出现了以下两种观点.
观点1:由于物体B在N点下方1m处为平衡位置,因此,物体B经过该点时加速度为零,速度达到最大.由题目所给条件可知此时滑轮左侧的绳子转过的角度为30°.这种观点得到了绝大部分学生支持.
观点2:当物体B到达N点下方1m处时,受力不一定平衡,因为物体A未必处于平衡状态,所以无法确定该点是否为B物体下滑的最大速度所在位置.这种观点只有很少几个学生赞同.
那么,到底两种观点谁是谁非呢?
分析:设物体下落时左侧绳子与水平方向夹角为θ,将B物体的速度v分解为沿绳子方向的分速度v1和垂直绳子方向的分速度v2(图2),则有
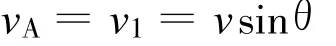
当B物体向下运动时 θ增大,可知即使B物体的速度v保持不变,A物体的速度vA也会随θ的增大而增大.

图2
假如观点1成立,即B物体在N点下方1m处受力平衡,速度最大,那么在B达到最大速度时的极短时间内,其运动可以看作是匀速运动,根据以上关系式可得,A物此时处于加速状态,绳中张力应该大于B物静止在该点时绳中的张力,即B物体在此处受力是不平衡的,这与假设矛盾.所以观点1错误,观点2成立.
但是,仅仅通过上面的定性分析仍然无法确定B物体最大速度所在位置.下面通过计算来确定这一位置.
由机械能守恒定律得

化简后得
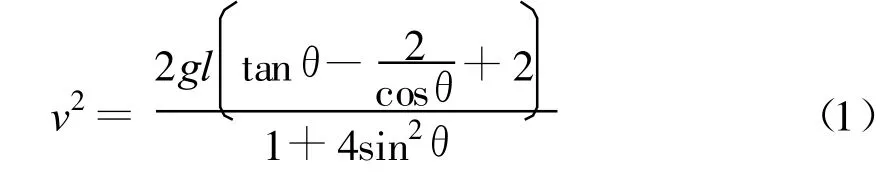
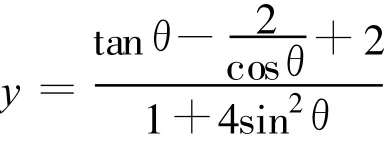
现在只需要讨论(1)式中的函数的单调情况.从数学角度看,求出该函数的一阶导数为零时的θ值,就能求得y的极值.但对此函数求导难度很大,而且即使求出来,也很难解出对应的 θ值.因此,想到用“几何画板”的函数功能进行研究.
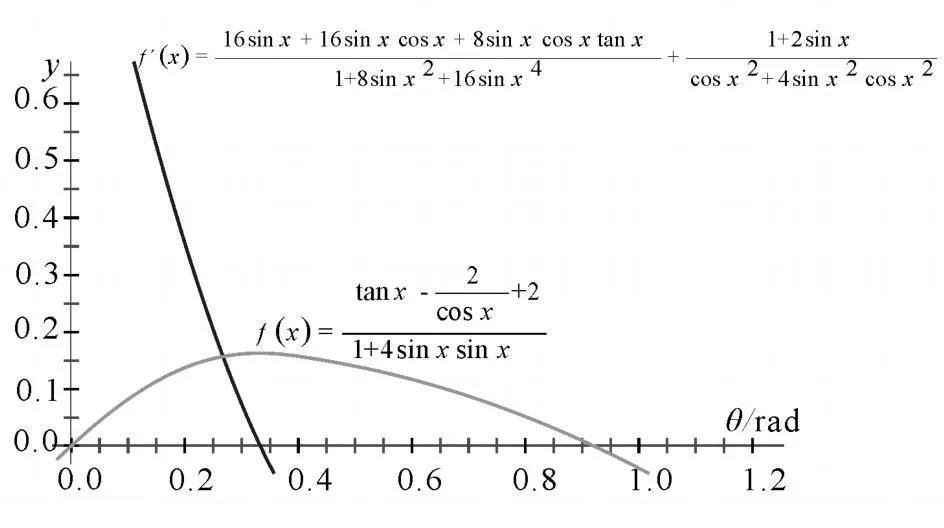
图3
建立函数:在“几何画板”中选择“图表”菜单的“新建函数”项,输入上面的函数(用x变量代替θ),确定后就能得到以上的函数表达式 f(x),然后选中此函数表达式,再选择“图表”菜单中的“导数”项,就可以由电脑完成对此函数的求导,得到导数表达式 f′(x)(图3).但要解出 θ仍然很困难,因此,继续采用“几何画板”的图像功能来进一步研究.
绘制图像:选中这两个函数表达式,在“几何画板”中选择“图表”菜单的“绘制函数”,就得到了这两个函数的图像(图3).
由此图可以看出θ约为0.33rad,即θ=18.9°时B物体速度最大;并不是第一种观点中的30°时速度最大.
体会:“几何画板”具有强大的计算功能和图像功能,可以用来迅速有效地处理数据,展示物理规律,这给我们研究物理问题突破难点提供了一种有效途径.充分利用这些功能解决常规手段难以解决的物理问题,有利于推动信息技术在物理教学中的应用.同时,也提醒我们,在编题、选题时要有科学的批判精神,要注意检验,用实事求是的态度对待教学,不要仅仅采取“拿来主义”.
