K-原子能级移动与能级宽度的计算

梁春恬，李灵侠，戴芳欢

(天津城市建设学院 a. 基础学科部；b. 电子与信息工程系，天津 300384)

K-原子就是一个带负电的K介子(K-)进入原子外围轨道，通过放出 X射线退激发进入较低能级，最终落入原子核，被原子核吸收.此时 K-介子的地位有点像原子中的电子，只是 K-介子的质量比电子大得多，因而 K-介子轨道半径比电子轨道半径小得多；由于K-介子与核的表面靠得很近，因此K-介子与核之间除了库仑相互作用外，还有强相互作用[1].K-原子对研究者了解介子与原子核的强相互作用有着非常重要的意义.K-原子中强相互作用的存在带来的介子原子的能级移动ε (相对于无强相互作用时的能级)和能级宽度 Γ (核吸收的量度)是两个非常重要的物理量，在实验中可以测量[2].理论方面，K-原子满足 Klein-Gordon 方程，考虑 K-介子与原子核之间的强相互作用，引入合适的光学模型势，求解则可得到能级移动ε 和能级宽度 Γ.若理论计算结果与实验符合，就可以提取描述介子与原子核间强相互作用的势场，获取介子与原子核之间强相互作用的信息[3].

前些年，研究者从低能散射角度计算了相应的散射长度[4-6]，得出 K-与核间强相互作用的平均效果为吸引力；但近几年的实验结果表明，K-与核的强相互作用不是吸引力，而是排斥力[7-8].本文利用 DD(density dependent，简称DD)光学模型势，通过对K-原子 Klein-Gordon方程的数值求解，得到了 K-原子的能级移动ε和能级宽度Γ，其结果反映了DD光学模型势描述K-原子强相互作用的正确性.

1 DD模型

K-原子是具有自旋为0的原子体系，可用Klein-Gordon方程来描述[9]

式中：m为K--原子核的约化质量；B为K-介子在原子系统中的束缚能；Vopt(r)为描述 K-介子与原子核之间强相互作用的光学势，Vc(r)为 K-介子与原子核之间的库仑相互作用势，且

如果不考虑 K-介子与原子核之间的强相互作用，这时Klein-Gordon方程被简化为

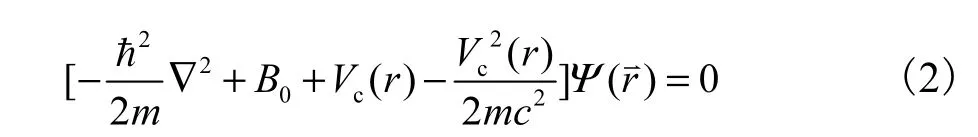
其中：B0为没有强相互作用时 K-介子在原子系统中的束缚能.

由于吸收效应的存在，Vopt(r)和 B都是复数.由方程(1)可以计算束缚能B的实部ReB和虚部ImB，由方程(2)可以计算束缚能 B0，则能级移动 ε和能级宽度Γ的计算如下

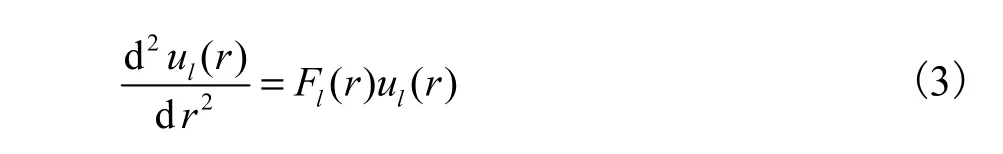
方程(3)可以通过数值方法求解[10].系数Fl(r) 在方程(1)中表示为

在方程(2)中表示为

Vopt(r)的表示采用DD模型的形式[11]

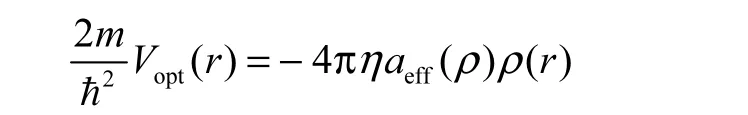
其中：η=1+mk/mN，mk为K-介子的质量，mN为所研究原子核的质量；aeff(ρ)为有效散射长度[7]

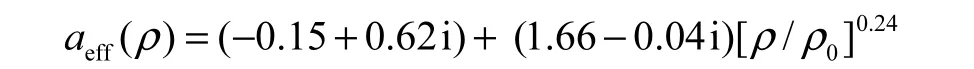
其中：ρ为核密度，本文通过相对论平均场(RMF)方法计算[12]

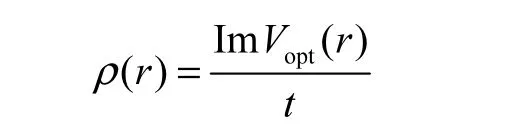
式中：t= 30 MeV· fm .

2 结果与分析

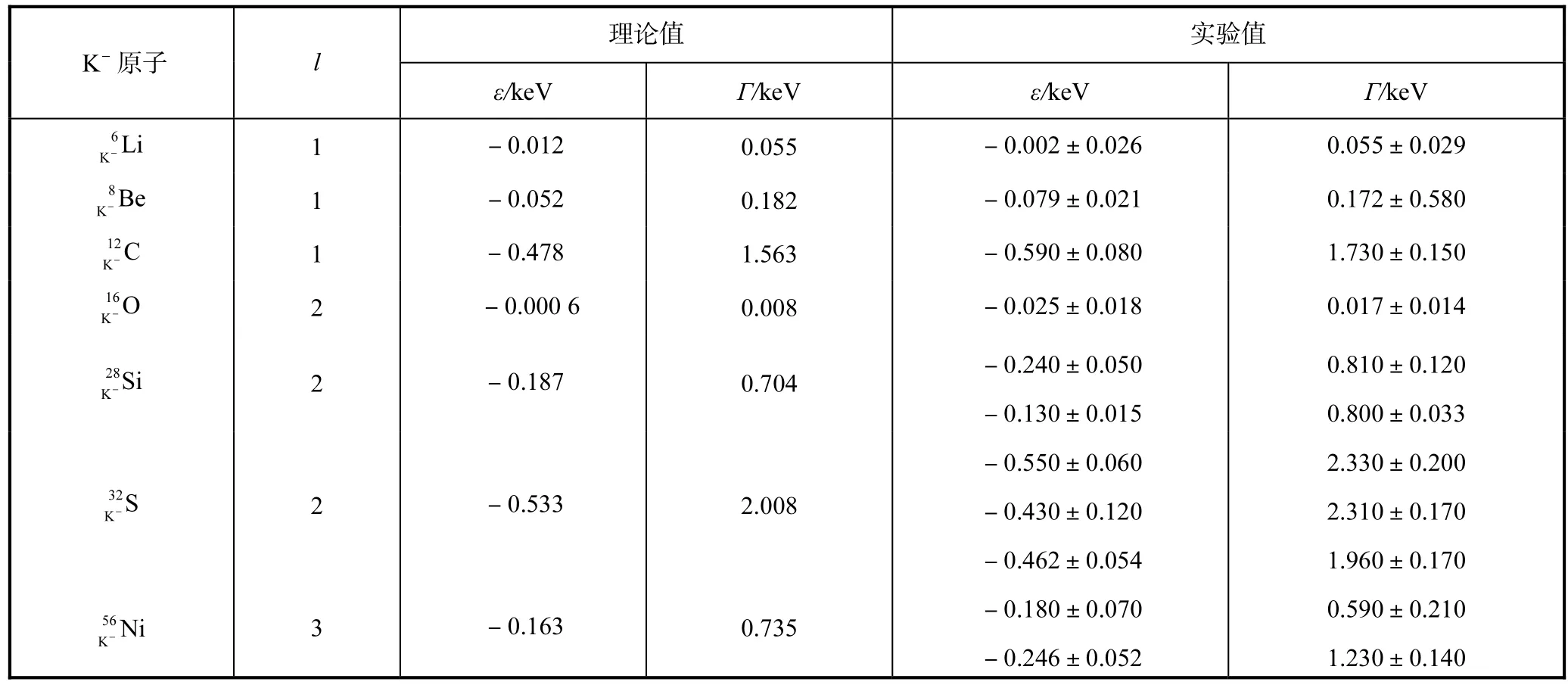
表1 K-原子的能级移动ε和能级宽度Γ理论值与实验值的比较

从表1可以看出，理论计算结果与实验数据符合较好．说明本文所采用的 DD模型可以很好地描述K-原子中K-介子与原子核之间的强相互作用．

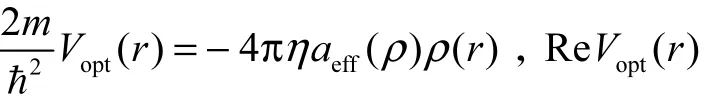
［1］王景丹，钟显辉，宁平治. 原子与原子核的新形态——介子原子和介子核[J]. 现代物理知识，2005，17：32-34.

［2］CARGNELLIA M，BAZZIB M，BEERC G，et al. Kaonic atoms studies at DAFNE by the SIDDHARTA experiment[J]. Nucl Phys，2010，A835：27-34.

［3］YAN Y，POONSAWAT W，KHOSONTHONGKEC K，et al. Kaonic hydrogen atoms with realistic potentials[J].Phys Rev，2010，C81：065208.

［4］FRIEDMAN E，GAL A，BATTY C J. The density dependent potentials and the strong interactions [J]. Phys Lett，1993，B208：6-12.

［5］BROWN G E，KUBODERA K，RHO M，et al. The scattering length from the evaluation on the low-energy scattering angle [J]. Nucl Phys，1994，A567：837-852.

［6］BATTY C J. Strange exotic atoms [J]. Nucl Phys，1995，A585：229-238.

［7］DABROWSKI J，ROZYNEKJ，ANAGNOSTATOS G S.Κ-atoms and ΣN interaction [J]. Eur Phys J，2002，A14：125-131.

［8］NOUMI H. Sigma-nucleus interaction in medium to heavy nuclei [J]. Nucl Phys，2003，A721：995c-998c.

［9］BATTY C J，FRIEDMAN E，GAL A. Strong interaction physics from hadronic atoms [J]. Phys Rep，1997，287：385-445.

［10］蔡崇海，李 磊. 束缚态径向方程和Ξ-超核的结合能[J]. 高能物理与核物理，2003，27：1005-1008.

［11］MIZOGUCHI M，HIRENZAKI S，TOKI H.Microscopic kaonic-atom optical potential in finite nuclei with Λ(1405)and Σ(1385)resonances [J]. Nucl Phys，1994，A567：893-918.

［12］FRIEDMAN E，GAL A，MAREŠ J，et al. K-nucleus relativistic mean field potentials consistent with kaonic atoms[J]. Phys Rev，1999，C60：024314.