二项分布的零频率估计

刘瑞香

(山西农业大学文理学院,山西太谷 030801)

二项分布是一种常见的离散型随机变量的分布,在许多场合有重要的应用,如在保险问题中应用非常广泛[1]。关于二项分布的参数估计问题常见的有矩估计和极大似然估计法,而零频率估计有许多好的性质。本文研究二项分布参数的零频率估计。

1 零频率估计

若离散型随机变量X有如下的概率分布:

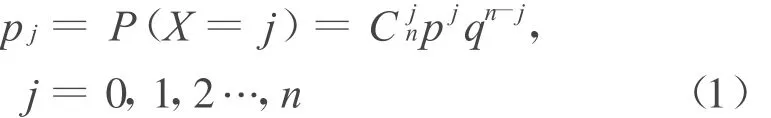
其中n＞0,0＜p＜1为参数,q=1-p,则称X服从参数为n,p的二项分布,记作B(n,p)[2]。

若X服从二项分布B(n,p),则X的数学期望E(X)=np,方差var(X)=nqp 。

零频率估计法就是用样本观测值中取零的频率来估计总体X取零的概率。

设总体X服从二项分布B(n,p),参数n,p未知,下面讨论n,p的零频率估计。

若x1,x2,……,x N为抽自二项分布B(n,p)总体X的随机样本,记 f i为样本观测值中取i的个数(或频数),i=0,1,2…,n。则样本观测值中取零的频率为样本均值

因总体X取零的概率为

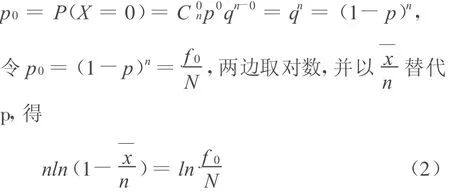
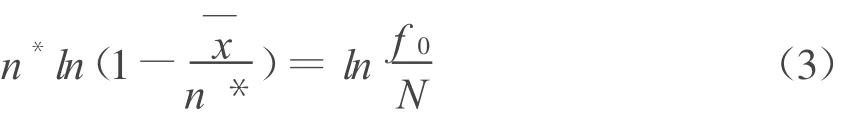
若方程(2)的解 n存在,唯一,记作n*,即则称n*为二项分布 B(n,p)参数n的零频率估计。此时为参数p的估计,且称(n*,p*)为二项分布B(n,p)参数(n,p)的零频率估计。

2 零频率估计的存在性与唯一性

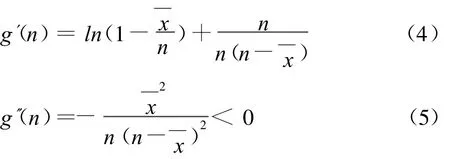
所以g＇(n)为n的单调减函数,且g＇(+∞)→0。从而,对任意的 n＞0,有 g＇(n)＞0 。故 g(n)为 n的单调增函数。又

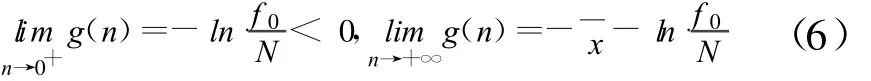
3 零频率估计的渐近正态性

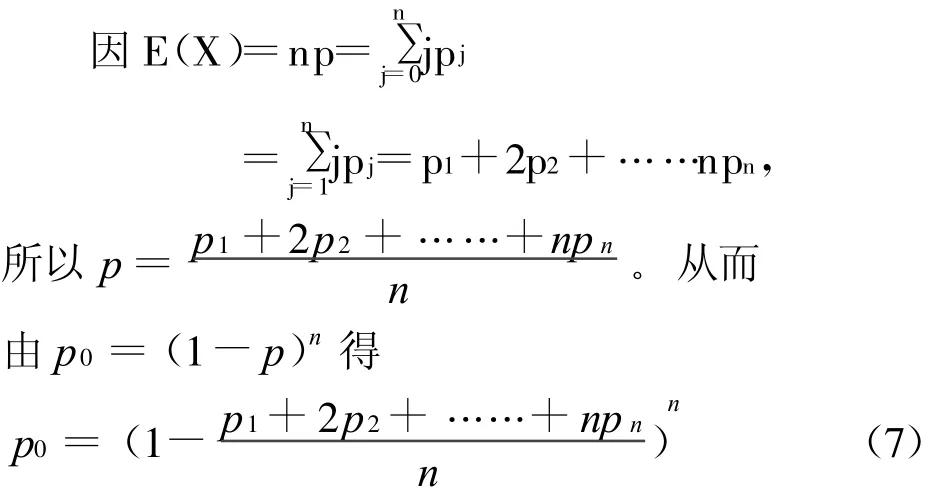
(7)式两边取对数,得

由方程(8)所确定的函数n=h(p 0,p 1,……pn)的一阶偏导数为:

其中

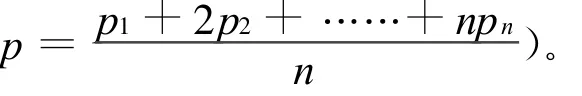
同理 ,得

由文献[3]第119页的公式(2.22),有

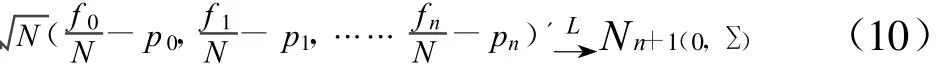
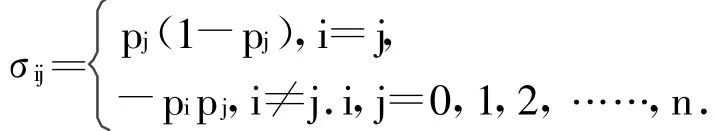
若n满足方程(8),n*为(3)的解,即

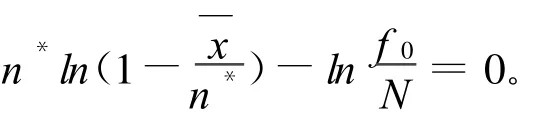
其中

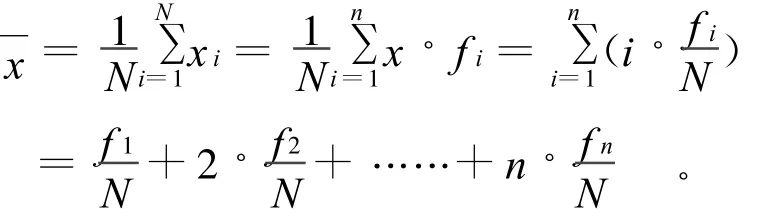
则由文献[4]第151页的定理4.3,有

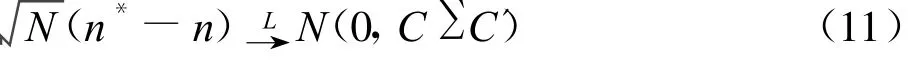
其中

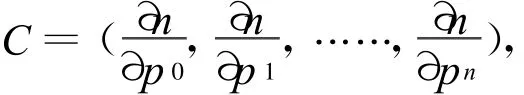
经计算,得

且

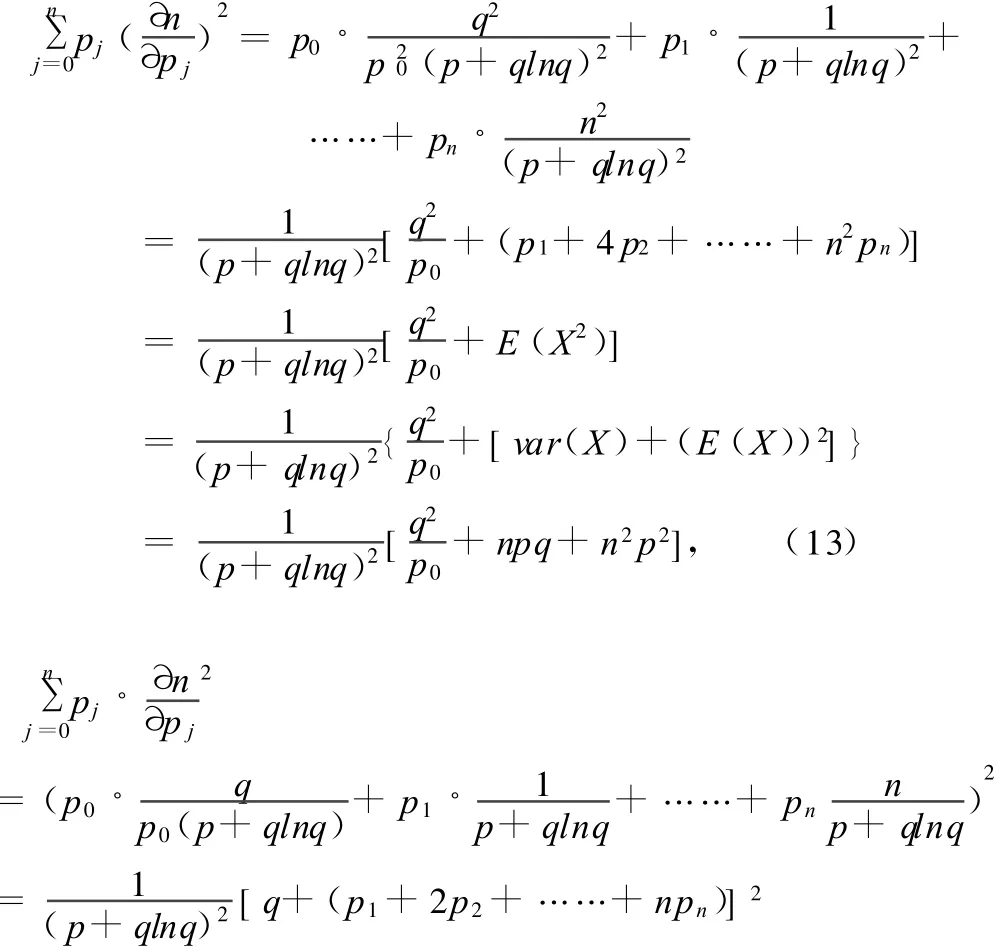
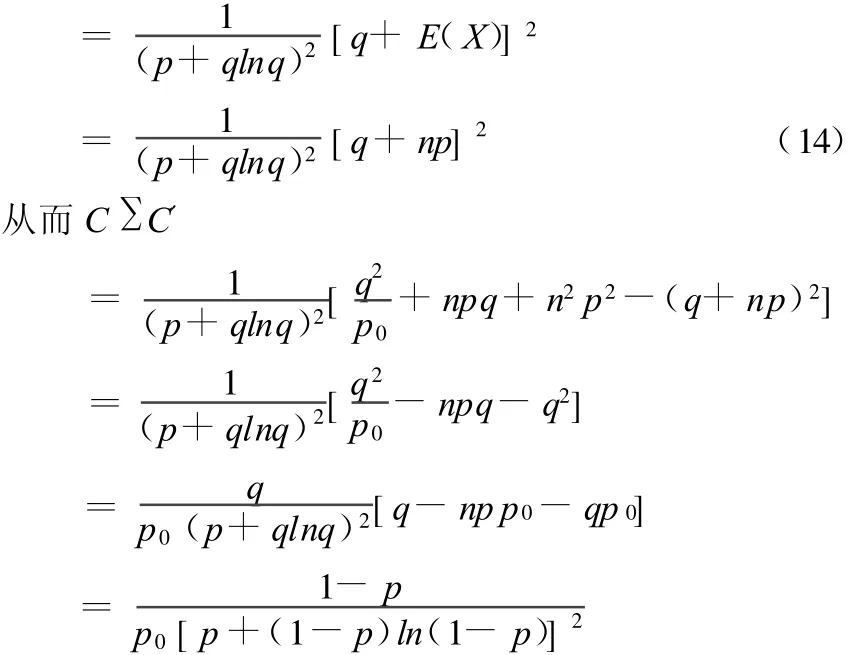
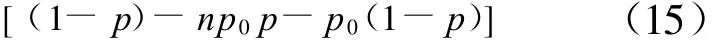
即

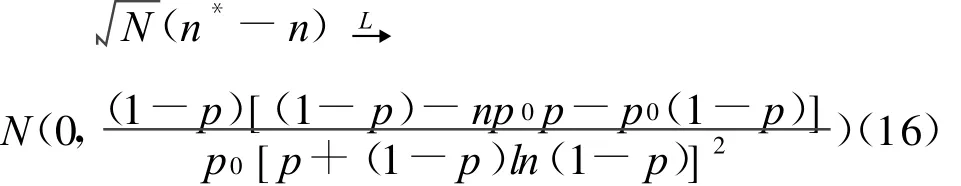
故N*有渐近正态性。

从以上得出的结果可以看出,零频率估计是一种很好的估计方法。进一步可以研究零频率估计与其他估计方法的优劣。

[1]于向红.二项分布的计算及其在保险问题中的应用[J].电大理工,2005,5(2):7-9.

[2]何书元.概率论[M].北京:北京大学出版社,2006:58-59.

[3]茆诗松,王静龙,濮晓龙.高等数理统计[M].北京:高等教育出版社,1998:119-120.

[4]陈希孺.高等数理统计学[M].合肥:中国科学大学出版社,1999:151-152.