二元含参量正常积分函数的分析性质

顾先明

（唐山师范学院 数学与信息科学系，河北 唐山 063000）

1 引言及预备知识

众多数学分析类教科书[1-4]都对含参量正常积分做了比较细致的研究，并得出了含参量正常积分在定义域上满足一定条件后可以具有连续性、可微性和可积性等不错的结果。之后的研究主要集中在对含参量正常积分已有的性质的推广和深化[5-9]，而对于含参量正常积分中的被积函数的进一步推广研究不是很多。笔者发现如果将含参量正常积分中的被积函数推广到三元函数（甚至是n元函数）后也会得到一些类似的结果。本文将含参量正常积分中的被积函数推广到三元函数后定义了一类二元含参量正常积分函数，并重点讨论其具有的分析性质。

定义 1 设 f( x,y,z)是定义在闭长方体区域D=[a,b]×[c,d]×[g,h]上 的 的 三 元 函 数 ， 当(x, y)∈ [a,b]× [c,d ]上取某定值，函数 f (x,y,z)就是定义在[g,h]上的以z为自变量的一元函数，倘若这时f(x,y,z)在[g,h]上可积，则其积分值是(x,y)在有界区域[a ,b ]× [c,d]上取值的二元函数，记它为I(x,y)，则有

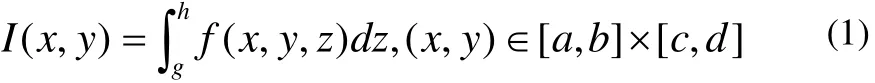
我们把形如(1)的函数叫做二元含参量正常积分函数。

定义 2 设区域 D ⊂ R3， f:D →R，如果∀ε＞0，∃δ ＞ 0，使得对任意的点 (x1, y1, z1)，( x2,y2, z2)∈D， 并且当

时，有

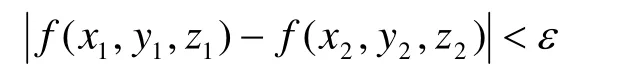
则称f在D上一致连续。

引理 1 若函数 f (x,y,z)在有界闭区域 D⊂ R3上连续，则函数 f在D上一致连续。

引理 2 若函数 f (x,y,z)是定义在有界闭区域D上的连续函数，那么该函数必在该有界闭区域D上可积。

2 主要结果及证明

定理 1（连续性） 若三元函数 f (x,y,z)在闭长方体区域 D=[a,b]×[c,d]×[g,h]上连续，则函数

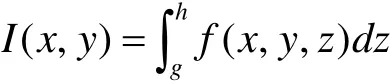
在区域 E= [a,b] × [c,d ]上连续。

证明 设 ∀(x, y)∈ [a,b]×[c,d ]，对充分小的Δx,Δy，令(x+Δx,y+Δy)∈[a,b]×[c,d ]（若(x,y)为矩形区域的边界，则仅考察的情形），于是

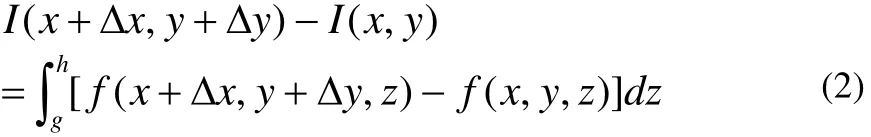
由于 f (x,y,z)在有界闭区域D连续，从而一致连续。即 对 ∀ε ＞0, ∃δ ＞0。 对D内 任 意 两 点 (x1, y1, z1)，(x2,y2,z2)，只要

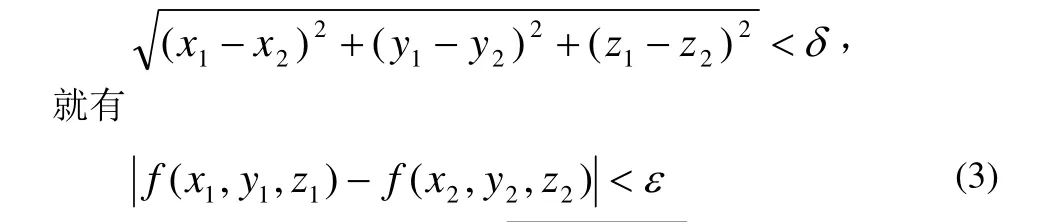
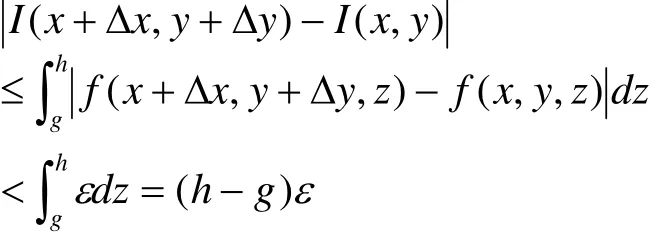
这就证得I(x,y)在 E= [a,b ]× [c,d ]上连续。

注 对于定理1的结论也可以写成如下的形式：

若f (x,y,z )在闭长方体区域D上连续，则对∀(x0,y0)∈[a,b ]×[c,d]，都有

定理2 若函数 f (x,y,z)与其偏导数

都在闭长方体区域 D=[a,b]×[c,d]×[g,h]上连续，则

分别关于x,y在区域 E= [a,b] × [c,d ]上可微，且

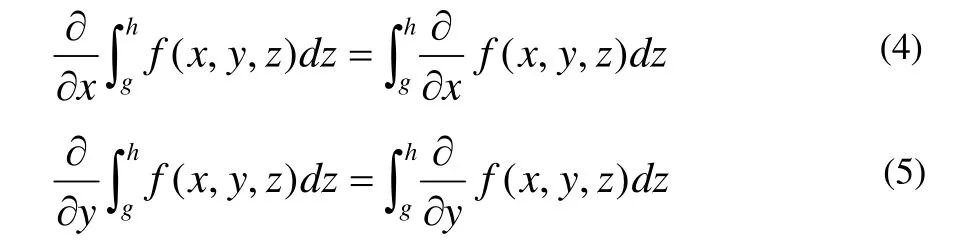
证明 只证明其中之一，另一个可类似证明，证明(4)。

对 区 域 E= [a,b] × [c,d]内 任 意 一 点(x,y)， 设(x+Δx,y+Δy)∈[a,b]×[c,d ]，则

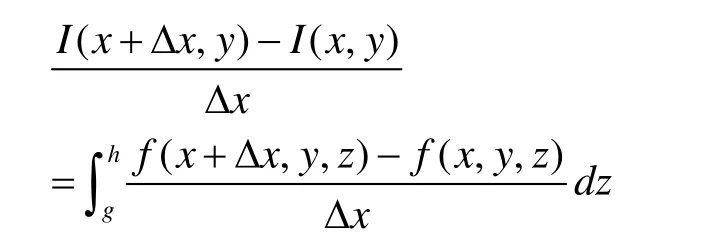
由微分中值定理（拉格朗日中值定理）及

在有界闭域D上连续（从而一致连续），对 ∀ε ＞0, ∃δ ＞0只要＜δ时，就有

其中θ ∈ (0,1)，因此

这就证得对 ∀(x, y)∈ [a,b]×[c,d ]，有

根据文献[10]所给出的“多元函数可微的充要条件”的结论影响，可以进一步加强上述的定理2。

定理3 （可微性） 二元含参量正常积分函数

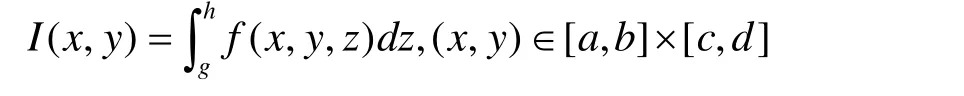
在点 M ( x0, y0)可微当且仅当I(x,y)在 M ( x0, y0)处偏导都存在，且 ∀ε ＞0, ∃δ ＞0，当时，有

证明 （必要性）已知函数I(x,y)在点 M ( x0, y0)处可微，故 Ix(x0,y0),Iy( x0, y0)都存在，且

令h=(6)式，则当

当ρ→0时，(7)→0，从而当 (x, y)→ ( x0, y0)时，对∀ε ＞0,∃δ ＞0时，当0时，有

（充要性）已知函数I(x,y)在点 M ( x0, y0)处的偏导数都存在，且对 ∀ε ＞ 0， ∃δ ＞ 0，当时，便有

则当ρ→0 时

于是当 (x, y)≠ ( x0, y0)时，

易知当ρ→0 时，(8)→0，故

由二元函数在一点可微的定义可知，二元函数u= I(x,y)在点 M (x0,y0)处可微。

定理4（可积性） 若 f (x,y,z)在闭长方体区域

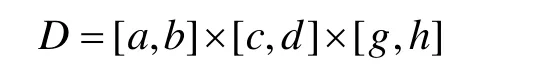
上连续，则I(x,y)在有界区域 E= [a,b] × [c,d ]上可积。

证明 由定理 1已证得函数I(x,y)在有界闭区域E= [a,b ]× [c,d ]上连续，由引理2可知I(x,y)在有界区域E上可积。

定理5 若函数 f (x,y,z)在闭长方体

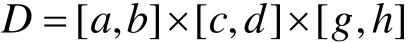
上可积，且对于任意的 (x,y)∈E =[a,b]×[c,d ]，定积分

存在，那么二元含参量正常积分函数I(x,y)在区域E上可积，并且

证明 对∀ε＞0，用平行于坐标面的平面网T做分割，它把D分成有限个小长方体

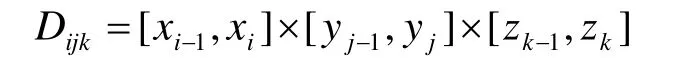
这时，我们也得到D的一个分割T1，设 Mijk,mijk分别为 f (x,y,z)在Dijk上的上、下确界，则对于

因为函数 f (x,y,z)在长方体区域

上可积，故∃δ＞0，使T ＜δ时，有

从而，根据可积的充要条件可知I(x,y)在D上可积，且

又由文献[11]中的定理21.15可知

于是综合上述证明过程可知

事实上，从上述定理的证明过程来看，我们还可以将含参量正常积分中的被积函数中的自变量的个数作进一步推广，它仍然具有类似的连续性、可微性以及可积性等结果，这里就不再赘述。