修正的土体等温水分扩散系数求解方法探讨

谈云志, 刘晓玲

(三峡大学三峡库区地质灾害教育部重点实验室,湖北宜昌 443002)

地表路基所受地下水的作用是长期反复的过程,特别是在地势低洼或地下水比较丰富的地段,对于具有水敏性的红黏土,地下水位的涨落对其影响更加剧烈,而红黏土分布的区域多属炎热多雨地区,因此地下水对红黏土路基的作用问题得到关注[1-4]。地下水对路基影响的本质是非平衡基质势与毛细效应引起水分迁移后土体强度发生了弱化。红黏土路基中地下水分毛细上升的规律是有效分析和治理路基病害的根据。

等温水分扩散系数可用来评价地下水在路基中的毛细上升性状,直接利用该系数的物理定义求解存在很多难以测量的物理量,通过试验方法确定成为一种有效手段。文献[5]利用水平吸渗试验测试了该系数;文献[6]利用γ射线连续3个月测试了水平封闭土柱含水量随时间的变化规律,计算了其等温水分扩散系数;文献[7]利用同样的方法进行了这方面的测试工作,很显然土样水平放置时没有考虑重力对水分迁移的影响。但地下水向路基迁移是一个竖直上升的过程,重力的影响还有待商榷。

1 等温水分扩散系数的推导

试样来源于厦门至成都高速公路湖南省郴州段内,试样的基本性质见文献[4]。根据路基压实度控制标准制备不同干密度的圆柱土样,然后竖直放在等温水分扩散系数试验装置上,如图1所示。让试样底部在某一瞬间吸水,试样底部与透水石接触,通过不断提供水源使该端部很快就能达到或接近土样的饱和含水量,并在整个试验过程中保持这一含水量值不变。

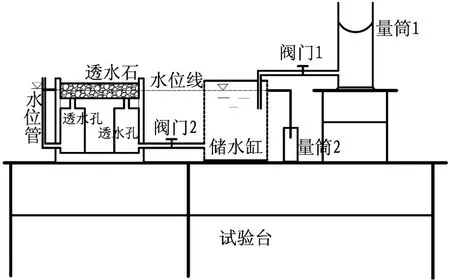
图1 等温水分扩散系数试验装置

水分在毛细势和基质势的作用下向上运动,该运动过程可以利用(1)式进行描述。从达西定律和连续性方程可以推导出非饱和多孔介质中的流动方程[5]为:

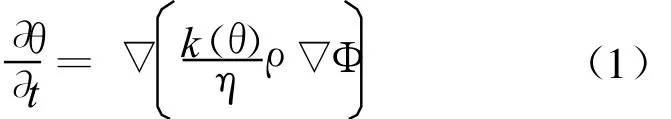
其中,θ为土壤体积含水量;ρ为流体密度;η为流体黏滞系数;Φ为水势;k(θ)为非饱和渗透系数。

对于竖直向的一维情况,(1)式变为:

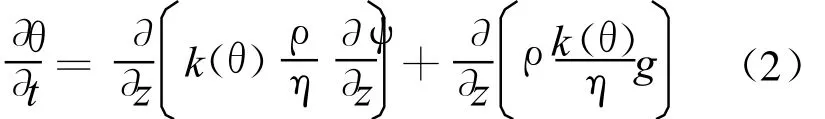
土水势可以看成由重力势和压力势(ψ)组成,文献[8,9]指出,可以把简化的热扩散系数及渗透系数概念应用到(2)式中,因而可得:

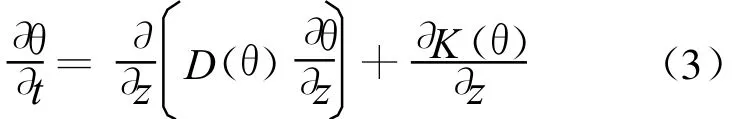
根据上述测试方法,其边界条件可以表示为:

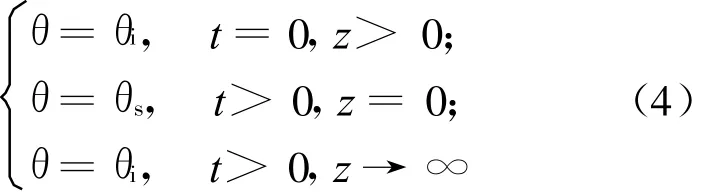
当把θ当作独立变量时,则可以换成以坐标z(θ,t)为函数的方程,即

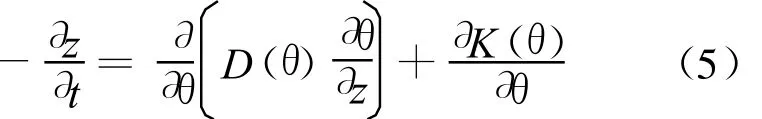
其中,t为时间。

利用分离变量法对(5)式进行转换,现假设z(θ,t)=β(t)κ(θ),代入(5)式得 :

方程的左边是变量t的函数,而右边是变量θ的函数,且在0≤z＜∞上均成立,所以两端相等必须同为一个常数,设为c。则有:

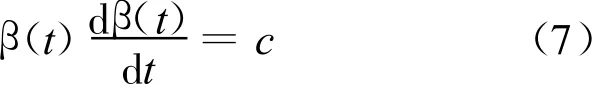
对(7)式进行积分得:

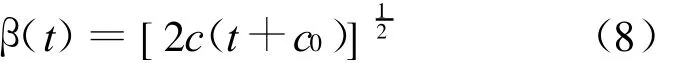
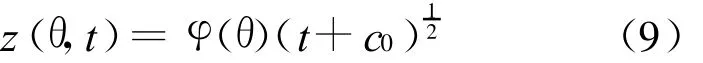
将(9)式代入边值条件(4)可得:

水分在土壤中扩散实际存在一个极限高度,故(11)式应为一个常数,所以c必须为零或者是无穷大。当c为无穷大时,(11)式就为零,与实际情况不符,因此,c只能为零。

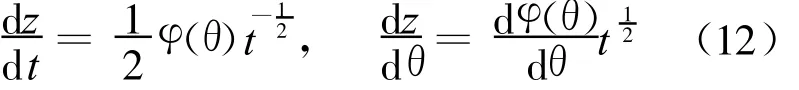
将(12)式代入 z(θ,t)=β(t)κ(θ),得 :

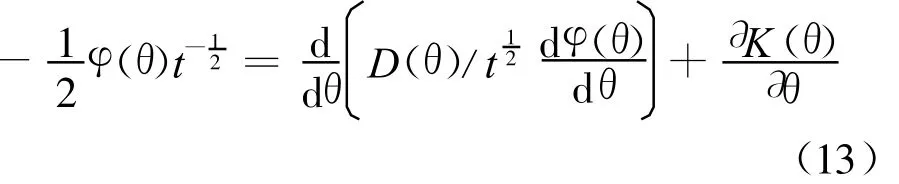
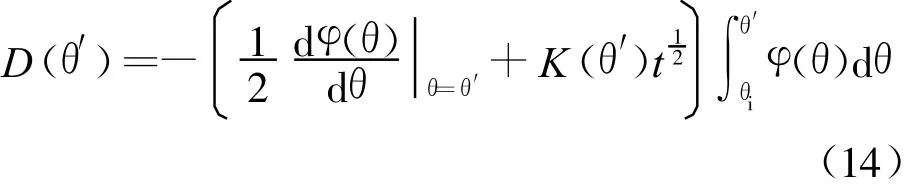
从(15)式可看出,只要已知试验在某一终止时刻(t=t0)时土壤含水量沿竖直方向的分布及土壤的非饱和渗透系数,就可以通过数学方法求得在某一含水量θ′下的等温水分扩散系数。

2 非饱和渗透系数的推导

通过严格的非饱和土室内试验来测定非饱和渗透系数,是一项十分耗时且对操作者要求很高的工作,通过土水特征曲线来预测非饱和渗透系数是解决这个难题的间接方法。文献[10,11]建立了土水特征曲线与导水系数的关系经验方法,即

其中,n、B为经验系数;θ为体积含水量。

当体积含水量为土水特征曲线进气值对应的含水量或饱和体积含水量θs时,则ks=Bθns,利用饱和导水率作为归一化因子,对(16)式归一化后得非饱和渗透系数为:

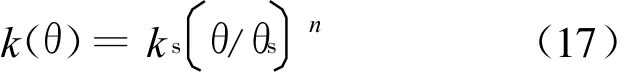
把(17)式代入(15)式便可求出某一含水量对应的考虑重力影响的等温水分扩散系数。

3 试验结果验证

按照(15)式计算扩散系数D(θ)的方法,对土柱中含水量沿高度的分布曲线先拟合,对拟合后的数据分别进行微分和积分。通过计算得出水分扩散系数与含水量的关系,如图 2所示。由图2可看出,扩散系数随含水量的变化呈单峰形状,故采用高斯公式对其试验数据进行拟合得:

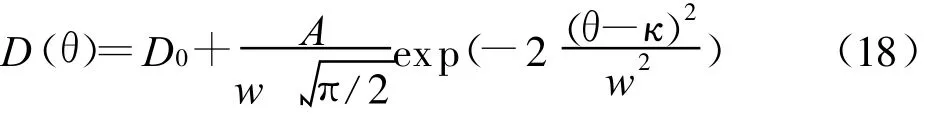
其中,D0、A、w、κ为拟合参数。拟合时D0取0。

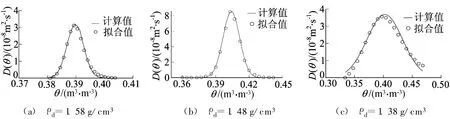
图2 扩散系数与体积含水量的关系

扩散系数公式参数的拟合结果见表1所列。

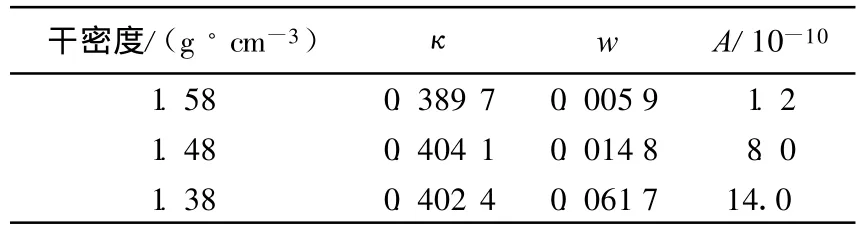
表1 拟合参数

从图2可知,水分因毛细效应扩散的能力随含水量的变化存在一个最优的含水量点,孔隙中的水分太多或太少都不利于水分的扩散。

4 结束语

路基在地下水的毛细上升作用过程中,重力对其水分迁移的影响不可忽略。本文在水平入渗试验得出的等温水分扩散系数基础上,推导了考虑重力影响的等温水分扩散系数。该系数只要已知试验在某一个终止时刻(t=t0)时土壤含水量沿竖直方向的分布及土壤的非饱和渗透系数,就可通过数学方法求得在某一个含水量θ′下对应的系数值,最后利用自制的仪器分析了3组不同干密度的试样,验证了上述求解扩散系数的方法。

[1] 赵颖文,孔令伟,郭爱国,等.广西原状红黏土力学性状与水敏性特征[J].岩土力学,2003,24(4):568-572.

[2] 赵颖文,孔令伟,郭爱国,等.广西红黏土击实样强度特性与胀缩性能[J].岩土力学,2004,25(3):369-373.

[3] 谈云志.非饱和红黏土三轴试验研究[J].合肥工业大学学报:自然科学版,2009,32(5):725-729.

[4] 谈云志.压实红黏土的工程特征与湿热耦合效应研究[D].武汉:中国科学院武汉岩土力学研究所,2009.

[5] Bruce R R,Klute A.T he measurement of soil moisture diffusivity[J].Soil Science Society of American Proceeding s,1956,20:458-462.

[6] Cassel D K,Warrick A W,Nielsen D R.Soilk-water diffusivity values based upon time dependent soil-water content distributions[J].Soil Science Society American Journal,1968,32:774-777.

[7] 任奋芝.温度梯度作用下非饱和土壤水分运动试验研究[D].武汉:中国科学院武汉岩土力学研究所,1991.

[8] Klute A.Some theoretical aspects of the flow in of water in unsaturated soils[J].Soil Science Society American Journal,1952,16:144-148.

[9] Miller E E,Miller R D.Theory of capillary flow:I.practical implications[J].Soil Science Society American Journal,1955,19:267-271.

[10] Brooks R H,Corey A T.Hydraulic properties of porous media[J].Colorado State University Hydrology Paper,1964,3(3):850-858.

[11] Brutsaert W.The permeability of a porous medium determined from certain probability laws for pore size distribution[J].Water Resources Research,1968,4:425-434.