巨型框架减振结构的动力时程分析
2010-10-25淦克丽盛宏玉叶献国
淦克丽, 盛宏玉, 叶献国
(合肥工业大学土木与水利工程学院,安徽合肥 230009)
0 引 言
近年来,随着社会技术进步和经济发展,人们已不再满足于大震不倒的抗震要求,结构控制获得了工程界的极大重视。结构控制可分为被动控制、主动控制、混合控制和半主动控制等,其中,以被动控制的研究和应用较多。被动控制的种类繁多,归纳起来,主要可分为基础隔震(如橡胶垫支座隔震、滑移型支座隔震等)、调频质量减振(如采用质量块、质量泵等)和阻尼耗能减振(如设置粘弹性阻尼器、铅挤压阻尼器等)。
巨型框架结构体系由主框架和次框架组成。主框架是以电梯和楼梯间等竖筒作为主框架柱,以每隔若干楼层设置的巨型梁作为主框架梁。巨型结构的发展由普通的巨型框架结构到巨-子型控制结构体系,直至后来改进到带附加柱的巨-子型控制结构体系。主框架是一种大型的跨层框架,每隔若干层设置一道巨型框架梁,每隔若干个开间设置巨型框架柱。主框架巨型梁之间的楼层另设柱网尺寸较小的次框架。主框架承担水平荷载和由次框架传来的竖向荷载,次框架只承担本身楼层的竖向荷载并传递给主框架,其水平荷载通过各楼层楼盖直接传递到主框架。由于巨型框架结构体积庞大,抗侧刚度及自重极大,因而将承受巨大的水平地震作用[1,2]。
为了降低巨型框架结构的地震反应,提高其抗震性能,本文采用层间隔震方案,用橡胶垫支座将最上端的2个次框架与主框架隔开组成减振结构体系,并与原来的抗震结构体系进行地震反应的对比分析。结构体系如图1所示。
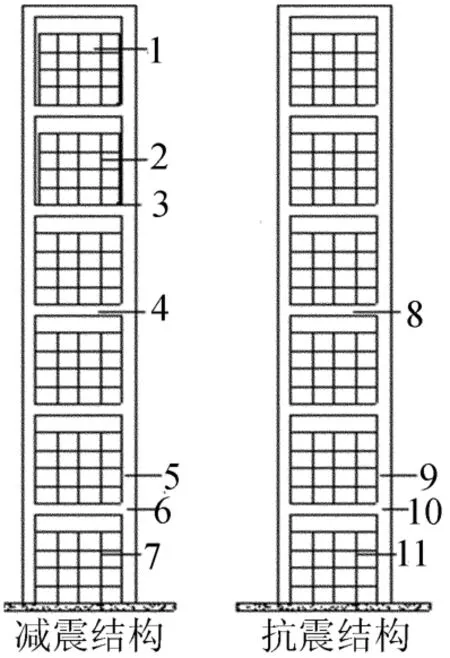
图1 结构体系
1 减振体系的结构动力模型建立
下面仅以2个子结构为例说明结构动力方程的建立过程[3],计算简图如图2所示。对于有任意多个隔震子结构的情况,推导过程与此类似。
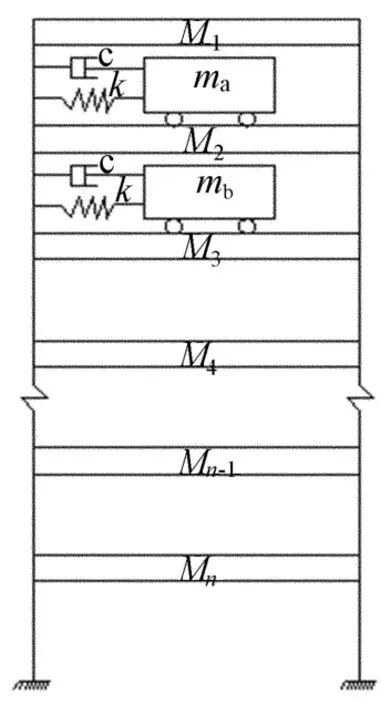
图2 计算简图
设地面某方向的运动加速度为¨xg,主框架与子结构A和子结构B分别用M个和N个隔震支座相连接。
将主框架、子结构A和子结构B的位移矢量分别划分为:xp=(xp0xpaxpb)T、xa=和。其中和以及和分别为连接主框架与子结构A和子结构B所用隔震支座两端的诸结点相对于地面的位移分量而组成的矢量。
在下面的推导过程中约定:上标或下标p表示主框架的有关量;a和b表示子结构的有关量;0表示主-子结构无直接关联的有关量。每个隔震支座的刚度系数和阻尼系数分别为kai、cai(i=1,2,…,M)和(j=1,2,…,N)。
主框架与2个子结构的运动方程可分别表示为:
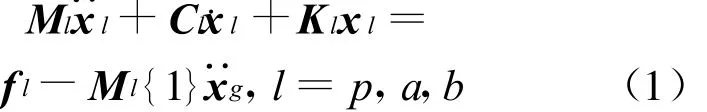
其中,质量矩阵和刚度矩阵可用分块矩阵表示:
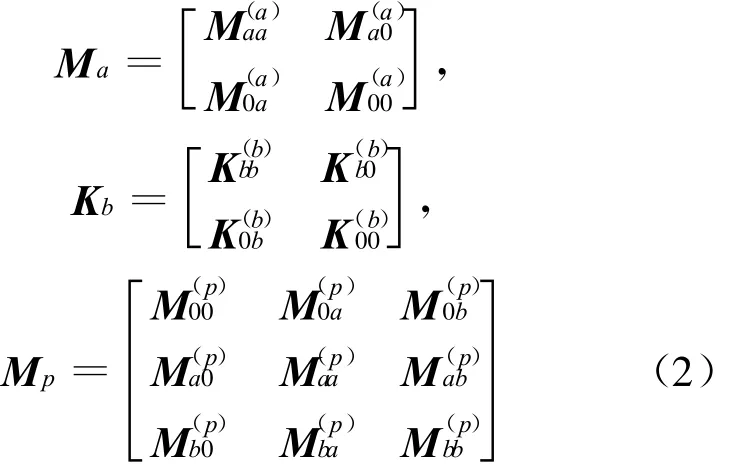
采用瑞雷阻尼模型,可将(1)式中的阻尼矩阵表示为:
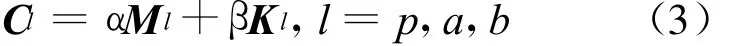
fl为主框架与子结构在隔震支座处所受到的反力矢量,也可分块表示为:
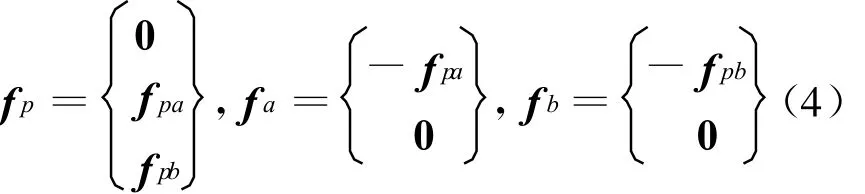
其中
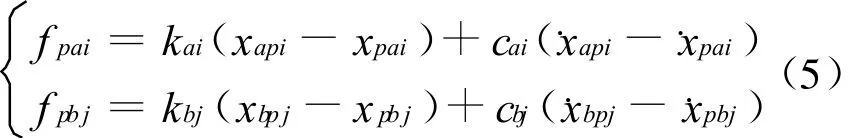
(5)式中,xapi和xpai分别为连接主框架与子结构A的第i个隔震支座两端的结点位移,其他符号的含义与此相同。
联立方程(1)~(5),可得整个结构体系的运动方程如下:
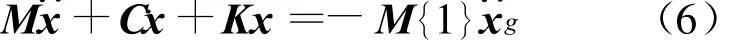
其中,矢量{1}为运动耦合矢量,其元素由0和1组成,即与地面运动相对应的自由度其值为1,其余为0。x为整个结构相对于地面的结点位移矢量,可分块表示为:
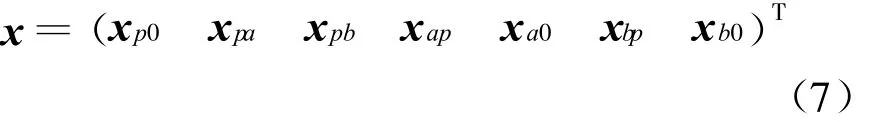
相应地,整个系统的矩阵也可分块表示为:
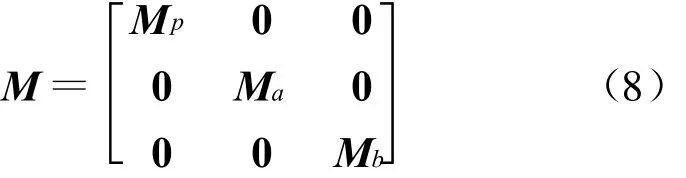
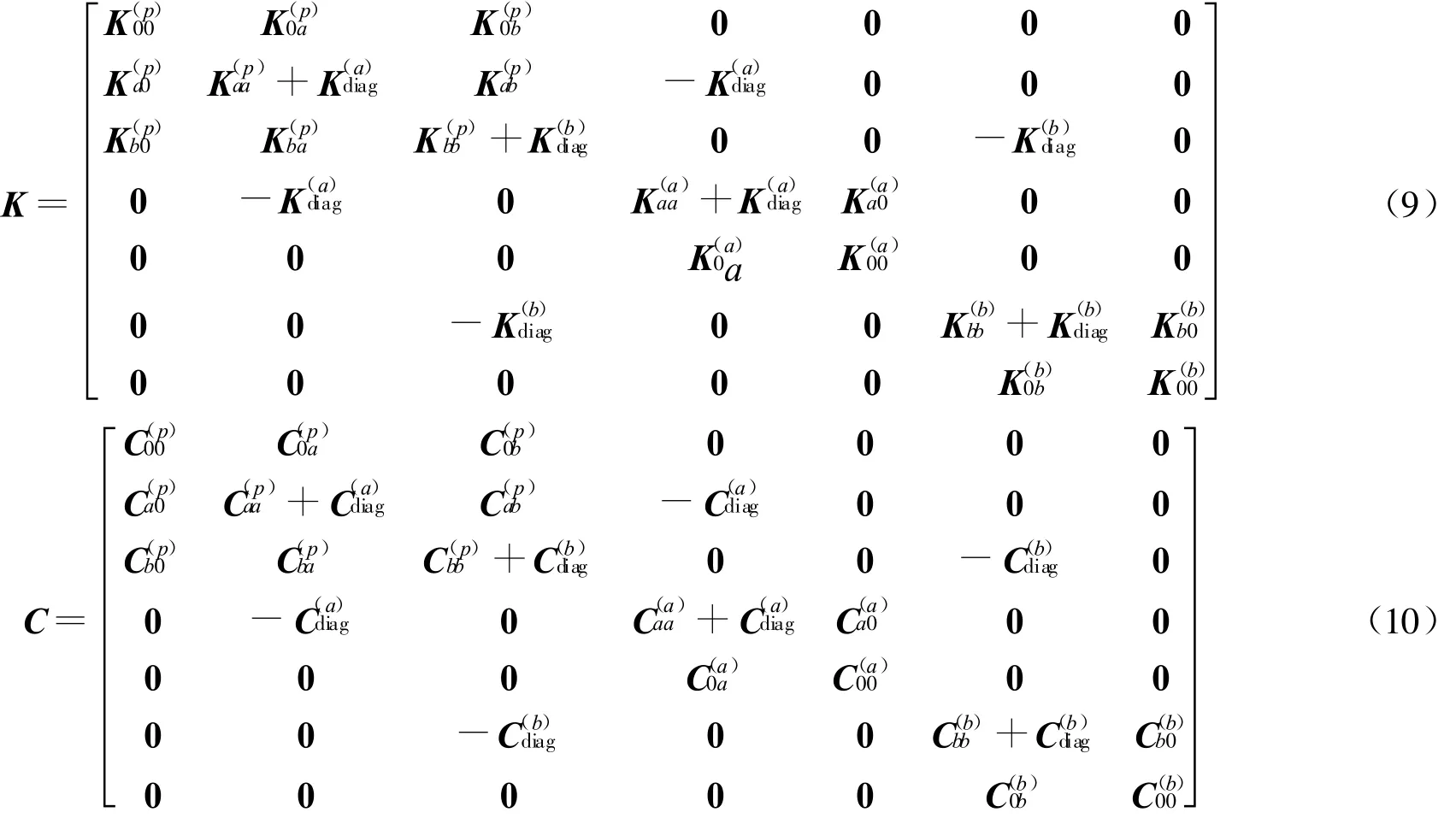
2 巨型结构算例分析
本文算例是主框架6层,次框架5层,主框架每层16 m,次框架每层3 m。巨柱和巨梁取2 m×2 m和0.8 m×2 m,混凝土强度等级C50,次框架的梁柱截面分别取0.25 m×0.5 m和0.5 m×0.5 m,混凝土强度等级C30。隔震支座放置在子结构A和子结构B的柱底(隔震支座布置见图3),总共58个,每个隔震支座的有效刚度为:193 kN/m,有效阻尼为:53.9 kN◦s/m[4-6]。
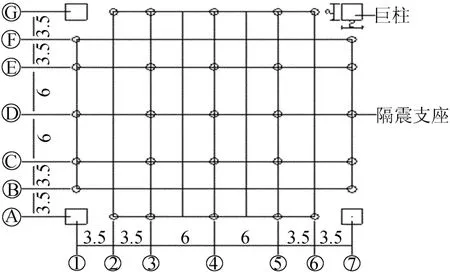
图3 隔震支座布置图
建筑类别为乙类建筑,设防烈度为8度,场地为Ⅱ类场地,根据有关规定[7],采用时程分析法时所用地震加速度时程曲线的最大值,多遇地震时为70 cm/s2。
根据SAP2000[8]中模态分析的结果,分别提取了抗震结构和减振结构前10阶自振周期并作对比,见表1所列。
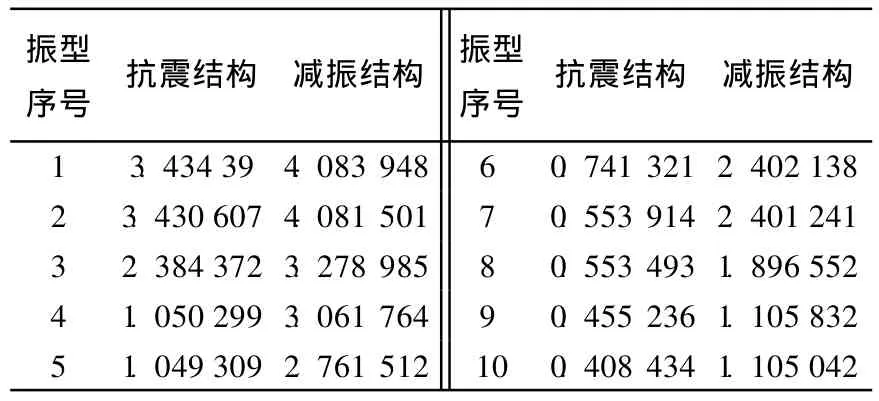
表1 抗震结构和减振结构自振周期对比
由表1可知,设置隔震支座后,结构的自振周期有所增加,抗震结构各阶振型的周期分布得比较离散,而减振结构各阶振型的周期分布得比较密集。
本算例采用一条地震波即El-centro波,时程计算时间为53.76 s。整理得出抗震结构和减振结构在地震作用下的主框架每层位移和主框架层间位移见图4和图5所示。
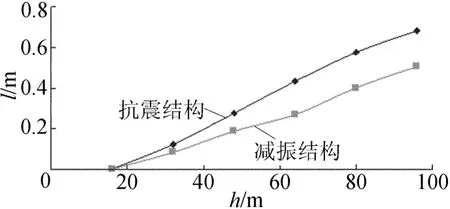
图4 主框架位移图
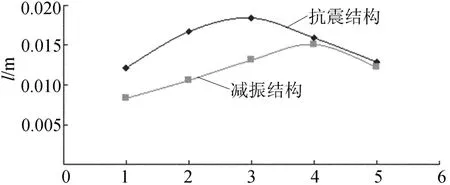
图5 主框架层间位移图
由图4、图5可知:
(1)减振结构的主框架位移有显著减小,越到结构的顶部位移减小的越明显。从主框架位移图可以看出结构的侧移曲线为剪切型。
(2)减振结构的主框架层间位移同样也有显著的减振效果,抗震结构主框架增加位移的最大值为0.018 43 m,对应减振结构的增加位移为0.015 12 m,减振效果可达17.96%。
图6所示是减振结构和抗震结构的顶点位移时程曲线图。
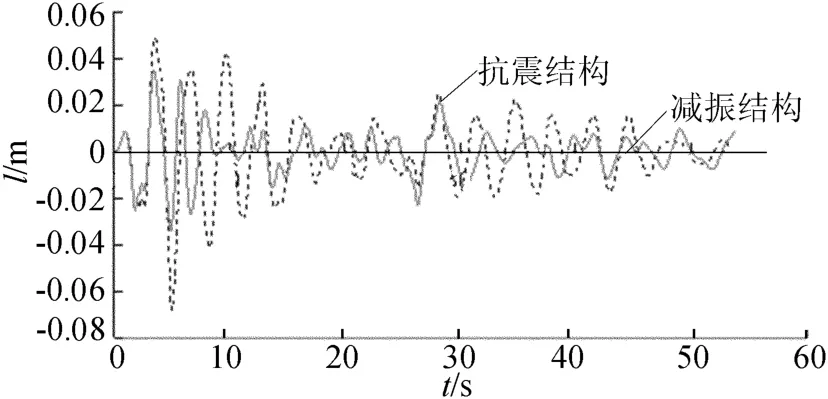
图6 结构顶点位移的时程曲线图
由图6可知:抗震结构主框架结构的顶点位移最大值为6.826 cm,减振结构的主框架结构的顶点位移最大值为5.066 cm。减振效果达到25.78%。
图7所示的是减振结构和抗震结构的基底剪力图。
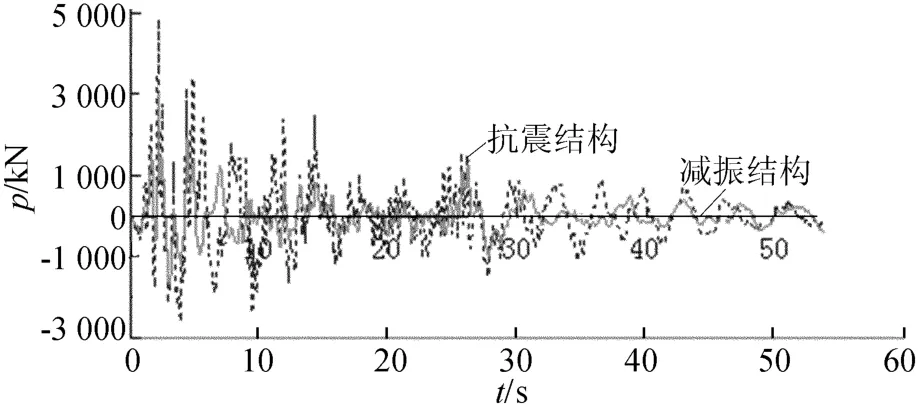
图7 结构基底剪力图
由图7可知,减振结构相对于抗震结构基底剪力有显著地减小,抗震结构的基底剪力最大值为4 826 kN,减振结构的基底剪力最大值为3 023 kN,减振效果达到37.36%。
3 结 论
在次框架和主框架连接处设置隔震支座,把巨型框架结构体系转变为一个大型的调频质量系统。其中每个子结构起着双重作用。一方面,它相当于体系中的一个巨大的调频质量块;另一方面,它又相当于具有基础隔震装置的多层框架结构。因此,减振结构具有多重减振功能。
本文采用有限元方法对巨型框架多功能减振结构进行建模,形成运动方程的过程可以采用子结构技术。采用子结构技术建模,但概念清楚可以较好地处理非经典阻尼结构的有限元计算问题。根据数值模拟的结果可以看出,减振结构与同等高度的抗震结构比较,有很好地减振效果。
[1] 蓝宗建,邹宏德,梁书亭,等.钢筋混凝土巨型框架多功能减振结构地震反应分析[J].建筑结构学报,2001,(4):77-83.
[2] 田玉基.巨型框架多功能减振结构的减振原理及优化设计方法[D].南京:东南大学土木工程学院,2002.
[3] 盛宏玉.结构动力学[M].合肥:合肥工业大学出版社,2005:10-147.
[4] 周福霖.工程结构减震控制[M].北京:地震出版社,1997:49-149.
[5] 日本建筑学会.隔震结构设计[M].刘文光,译.北京:地震出版社,2006:28-45.
[6] 刘文光.橡胶隔震支座力学性能及隔震结构的地震反应分析研究[D].北京:北京工业大学建筑工程学院,2003.
[7] GB50011-2001,建筑抗震设计规范[S].
[8] 北京金土木软件技术有限公司,中国建筑标准设计研究院.SAP2000中文版使用指南[M].北京:人民交通出版社,2006:450-486.
