基于经验模态分解的子带自适应声学回声消除算法

李 娜 陆晓明 陈盛云

（昆明理工大学信息与自动化学院,昆明 650051）

19世纪70年代至今,通信领域发生了翻天覆地的变化.传输方式上由最初的无线电报发展到后来的电话网,再到如今的移动通信网络；传输媒介由最初的无线电波,发展到同轴电缆,甚至光纤；交换技术也从电路交换的方式发展为现在的分组交换.人们在享受通信带来的便捷生活时,也一直受到回声现象的困扰,对于回声消除的研究一直以来都是科学家和技术家们探讨的课题.随着无线电话的广泛应用以及无线运营商之间的竞争,话音传输质量和客户服务成为用户评价运营商网络的关键因素.因此看来,对回声消除进行研究不仅具有理论意义,还能产生巨大的经济效益.

在学术研究上,国内外很多大学和研究机构都致力于自适应算法和滤波器结构的研究,并取得了很多成果.其中子带自适应滤波是当前研究的一个热点[1-2].Hallack[3]等人验证了子带方法应用在回声消除中较之全带方法能减少计算量、提高收敛速率；向赛辉[4]等人基于组合滤波器提出的组合算法实现两路回声的消除,合理分配了有限的资源；作者[5]基于小波变换提出的WL-APNLMS算法提高了收敛速率,计算复杂度较低.但是上述算法各有缺点,基于组合滤波器的组合算法收敛速率较慢,而基于小波变换的WL-APNLMS算法又要面临选择小波基的问题.近年来经验模态分解（EMD）已被引入自适应滤波器[6-7],EMD先对自适应滤波器的输入进行正交变换[8],减小了自适应滤波器输入向量自相关阵特征值的分散程度,大大增加了算法的收敛步长,提高收敛速度.较之于小波变换,EMD是一种采用自适应基的时频局部化分析方法,克服了小波变换需要选择小波基的问题.信号经EMD分解后每个IMF所包含的频率成分不仅与采样率有关,而且更为重要的是它还随着信号本身的变化而变化.因此,EMD是一种自适应的时频局部化分析方法,比小波变换更适用于回声这种非平稳信号的处理[9].

1 声学回声的产生及其消除原理

1.1 声学回声的产生

声学回声是由于扬声器与麦克风之间的耦合形成的,如图1所示.在无线电话,有线电话,以及扬声器电话的免提设备中都会出现声学回声.这些问题是由低质量的手机、周围环境中的回声（例如在汽车、旅馆或工厂中）或者电话听筒串话造成的.甚至高质量的手机也会出现声学回声,因为话音信号会通过用户的脸颊反射回麦克风.

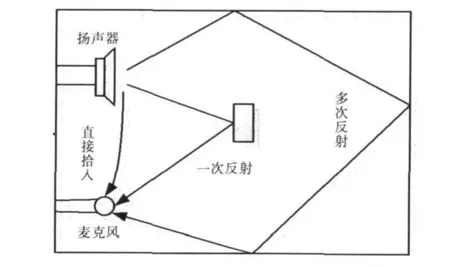
图1 声学回声的产生

1.2 声学回声消除原理

声学回声消除的原理如图2所示,图中的回声估计器和加法器是自适应滤波器的两个组成部分.h为回声路径的单位脉冲响应向量,输入信号x（n）在传输过程中产生回声信号d（n）为

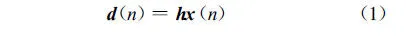
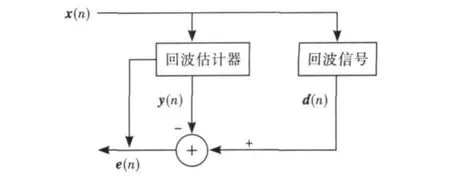
图2 声学回声消除的原理

y（n）是模拟回声路径产生的回声信号,其表达式为

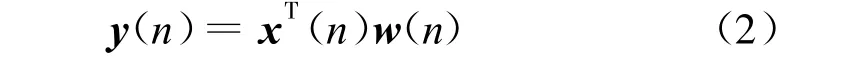
式中,x（n）=[x（n）,x（n-1）,x（n-2）,…,x（n-M+1）]T表示n时刻的输入信号矢量,由最近M个信号采样值构成,w（n）=[w0（n）,w1（n）,…,wM-1（n）]T表示n时刻自适应滤波器的系数矢量估值.

模拟的回声信号y（n）与真实的回声信号d（n）之差记为e（n）:

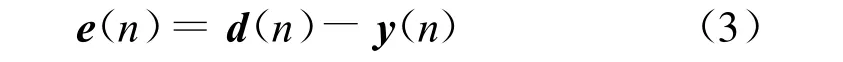
若自适应滤波器的单位脉冲响应向量h能很好地模拟回声通道的传递函数时,残留的回声信号e（n）就能达到最小,此时的声学回声就被抵消了.

2 子带自适应滤波

2.1 子带自适应滤波

因为语音信号是相关性很强的信号,很多实践证明用NLMS算法进行回声消除时,收敛速率较慢[10],而基于子带自适应滤波器的回声消除器设计则成为当前解决声学回声消除问题的主流方向.

子带自适应滤波器的原理是将输入信号被滤波器组划分成若干个子带,这些子带具有不同的频段[11],最后的误差信号是各个子带的回声误差信号的累加.图3是子带自适应滤波器的结构图.

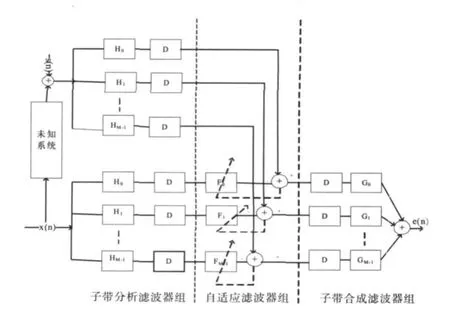
图3 子带自适应滤波器的结构图

如图 3所示,H0、H1、…、HM-1构成子带分析滤波器组；G0、G1、…、GM-1构成子带合成滤波器组；F0、F1、…、FM-1构成自适应滤波器组；子带的个数为 M,抽取因子为D,D＜M.

子带自适应滤波相对于全带自适应滤波的好处有以下几点:（1）在各个子带的自适应滤波过程中,滤波器长度是减少的,这使得子带滤波比全带滤波具有更大的计算效率.（2）由于在子带内语音信号的谱动态范围减少了,因而子带滤波将获得更大的收敛速率.（3）这种独立的结构使得所有的子带处理都能够并行实现,使系统性能更优.基于以上所提出的优点,本文提出的新算法也采用子带自适应滤波器用于消除回声.

2.2 基于组合滤器的组合算法[4]

该算法将语音信号分成5个频率段,H0（n）部分包含0～1000 Hz,H1（n）部分包含 1000～2000 Hz,H2（n）部分包含2000～3000Hz,H3（n）部分包含3000～ 4000 Hz,H4（n）部分包含 4000～ 8000 Hz,分段进行自适应回声消除,结构中用到3个分析滤波器组,在每个滤波器组的每个通道中进行了抽样,并在两路回声路径中分别加入了40dB的噪声,结构框图如图4所示.

图4 基于组合滤波器的组合算法的结构图

2.3 基于小波变换的WL-APNLMS算法[5]

将输入信号进行小波分解重构成低频（a5）和高频（d1～ d5）部分,再对 a5、d5 、d4 应用 APA 算法,而针对相对而言的高频部分d3、d2、d1则使用NLMS算法.最后将处理后的不同频段的信号相加即可得最终处理的结果.该算法的总体设计图如图5所示.

2.4 仿真结果

回声抵消效果一般采用回声返回衰减增益（ERLE）来评价[12],其定义如下:

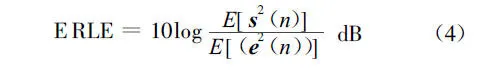
图5 基于小波变换的WL-APNLMS算法在回声消除中的总体设计

ERLE值越大,则表明e（n）越小,回声抵消效果越好,收敛快,一般要求ERLE＞6dB.

（1）输入信号波形.本文所采用的输入信号是用音频软件cool edit截取的一段wav格式的语音信号.信号长度N=5000,其波形如图6所示.

图6 输入的语音信号

（2）组合算法 、WL-APNLMS 、NLMS 、FAP 算法收敛速率的比较.仿真中,回声路径用式（5）脉冲响应来模拟,其中长度L=64,r（n）为幅度在-0.5～0.5之间均匀分布的随机向量,其值为rand（L,1）-0.5.

针对图6中的输入信号分别采用组合算法、NLMS、FAP算法,得到 ERLE曲线如图7所示.从图7可以看出,组合算法的收敛速率虽然已经达到了FAP算法的收敛速率,但较之WL-APNLMS算法则速率较低.WL-APNLMS算法虽然收敛速率较快,但它面临选择小波基的麻烦.这是因为小波分析是通过选择小波基进行分解的,其分解结果与所选的小波基密切相关.经验模态分解是一种采用自适应基的方法,可以避免选择小波基的麻烦,因此基于经验模态分解的自适应算法具有一定的优势.

图7 组合算法、NLMS、FAP算法 ERLE性能比较

3 基于经验模态分解的自适应算法（EMD-APNLMS）

3.1 新算法（EMD-APNLMS）在回声消除中的总体设计

如图8所示,将输入信号进行EMD分解为低频c1（n）、c2（n）、c3（n）、c4（n）、c5（n）、c6（n）和高频 c7（n）、c8（n）、c9（n）、c10（n）、c11（n）、res（n）部分.信号的频率高,采样率则低,导致采样点数少,算法的计算量就少.反之,信号的频率低,采样率则高,采样点数就多,计算量则大.为了降低算法的计算复杂度,本文对于不同的频段子带信号采用不同的自适应算法.为此,对于计算量少的较高频信号c1（n）、c2（n）、c3（n）、c4（n）、c5（n）、c6（n）采用计算复杂但收敛快的APA算法；对于计算量多的较高频信号c7（n）、c8（n）、c9（n）、c10（n）、c11（n）、res（n）采用计算简单但收敛慢的NLMS算法.那么整个处理过程中相对单独使用APA、NLMS算法,计算量较低.

图8 新算法（EMD-APNLMS）在回声消除中的总体设计

3.2 仿真结果

（1）将图6中的语音信号用经验模态分解.如图9 所示 .其中 c1（n）、c2（n）、c3（n）、c4（n）、c5（n）、c6（n）频率较高 ,c7（n）、c8（n）、c9（n）、c10（n）、c11（n）、res（n）频率较低.

图9 经验模态分解信号

（2）EMD-APNLMS算法的ERLE特性.

根据结构图图 8,对 c1（n）、c2（n）、c3（n）、c4（n）、c5（n）、c6（n）子带信号采用APA 算法；对c7（n）、c8（n）、c9（n）、c10（n）、c11（n）、res（n）子带信号采用 APA 算法.其中抽样因子D=8.仿真结果如图10所示.

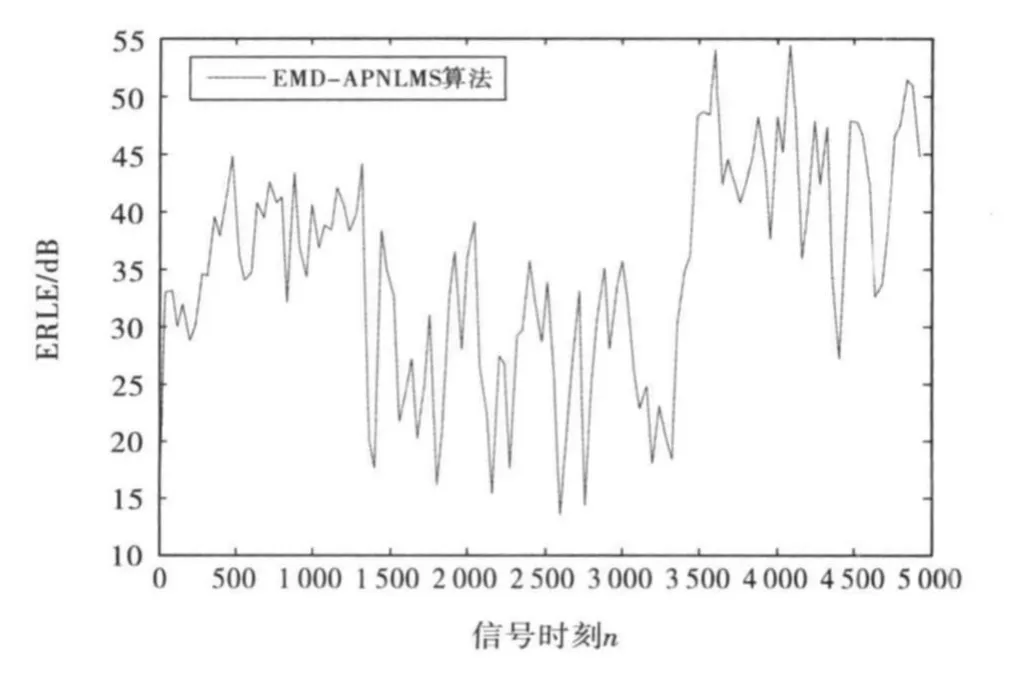
图10 EMD-APNLMS算法ERLE性能

（3）EMD-APNLMS、WL-APNLMS 、组合算法的ERLE特性比较,仿真结果如图11所示.由此可见,提出的EMD-APNLMS算法的收敛速率在0～1500时刻快于WL-APNLMS算法,1500时刻以后,与WL-APNLMS算法相当,又避免了 WL-APNLMS算法选择小波基的麻烦；新算法的收敛速率高于组合算法,克服了组合算法收敛较慢的缺点.

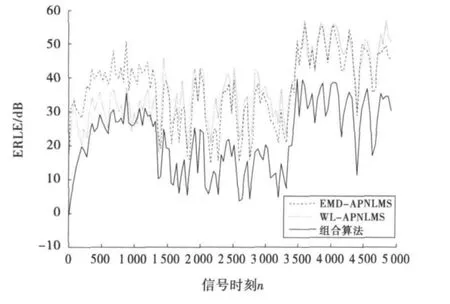
图11 EMD-APNLMS、WL-APNLMS、组合算法的ERLE特性比较

4 结 语

基于经验模态分解（EMD）的子带自适应滤波算法-EMD-APNLMS,实现了回声的良好消除,克服了NLMS遇到语音信号收敛速率慢的缺点,体现了子带滤波算法的优势.该算法较之组合算法有更好的收敛速率,并且该算法克服了WL-APNLMS算法选择小波函数的麻烦.

[1]M ayyas T,Aboulnasr T.A Fast Exact Weighted Subband Adaptive Algorithm and Its Application to Mono and Stereo Acoustic Echo Cancellation[J].Journal of The Franklin Institute,2005,342:235-253.

[2]Myllyla V.Residual Echo Filter for Enhanced Acoustic Echo Control[J].Signal Processing,2006,86:1193-1205.

[3]Hallack F S,Petraglia M R.Performance Comparison of Adaptive Algorithms Applied to Acoustic Echo Canceling[C].IEEE International Symposium on Industrial Electronics,2003（2）:1147-1150.

[4]向赛辉.电话会议系统中多路回声消除理论与应用研究[D].昆明:昆明理工大学,2008:12.

[5]李 娜,陈盛云,马 涛.一种新的基于小波变换的自适应算法在声学回声消除中的应用[J].四川师范大学学报:自然科学版,2009,32（1）:32-34.

[6]孔国杰,张培林,徐龙堂等.基于经验模态分解的自适应滤波算法及其应用[J].信号处理,2009,25（6）:958-962.

[7]钱 勇,黄成军,戚 伟.基于经验模态分解的自适应滤波算法在局部放电窄带干扰抑制中的应用[J].继电器,2006,34（22）:27-31.

[8]万 建.基于HHT语音识别技术研究[D].哈尔滨:哈尔滨工程大学,2006.

[9]徐 双,刘增力,丁 锐.基于希尔伯特黄变换方法的非平稳信号仿真与分析[J].昆明理工大学学报:理工版,2009,34（1）:108-112.

[10]Breining C,Drescitcl P,Hansler E,et al.Acoustic Echo Control:An Application of Very-High-Order Adaptive Filters[M].IEEE Signal Processing Magazine,1999:42-69.

[11]Sheila S,Hemami,Robert M.Gray.Subband Filters Optimized for Lost Coefficient Reconstroction[J].IEEE Trans on Signal Processing,1997,45（3）:10-14.

[12]Gansler T,Gays L,Sondhi M,et al.Doubletalk Robust Fast Converging Algorithms for Network Echo Cancellation[J].IEEE Trans.On Speech and Audio Processing,2000,8（6）:656-663.