星形两嵌段共聚高分子薄膜微相分离的耗散粒子动力学模拟

徐 毅, 冯 剑

(1.上海大学环境与化学工程学院,上海 200444;2.滁州学院化学与生命科学系,安徽滁州 239012)

星形两嵌段共聚高分子薄膜微相分离的耗散粒子动力学模拟

徐 毅1, 冯 剑2

(1.上海大学环境与化学工程学院,上海 200444;2.滁州学院化学与生命科学系,安徽滁州 239012)

利用耗散粒子动力学模拟研究两类典型的星形两嵌段共聚高分子薄膜的微相分离行为,观察到一系列有序结构,并获得相应的相图.结果表明:(Ax)4(By)4体系的相图比 (AxBy)4体系具有更明显的对称性,且前者比后者更易发生相分离,这与体相中的情况相近,而同等条件下,后者比前者更易形成岛状结构;组成相同的星形共聚高分子体系在体相与薄膜中所形成的介观结构之间存在对应关系,且一维受限能够使得该体系所形成的微相分离结构更为多样化;较小的薄膜厚度与较强的A-B组分间的排斥作用均有利于增强所形成结构的有序性.

星形两嵌段共聚高分子薄膜;微相分离;耗散粒子动力学

Abstract:M icrophase-separating behaviors of two typical star-diblock copolymer films have been investigated using the dissipative particle dynamics(DPD)technique.A seriesof ordered structures and corresponding phase diagrams have been obtained.Results show that,compared to(AxBy)4,the phase diagram of(Ax)4(By)4is distinctly symmetric. It is easier to carry out phase-separating for the latter than for the former,similar to their behaviors in bulk.Additionally,it is easier for the island phase to appear in(AxBy)4filmsunder the same conditions.Some structures formed in bulk and film at the same composition fraction can correspond to each other to a certain extent,and one-dimension confinement can make these systems form more kindsof microphase-separating structures.Besides,both thinner film and stronger A-B repulsion can contribute to enhance the order of relevant structures.

Key words:star-diblock copolymer film;microphase separation;dissipative particle dynamics

由于嵌段共聚高分子能够形成层状、柱状、球状以及双连续等一系列微相分离结构[1-2],从而具备了独特的优良性能并得到广泛应用[3-4],因此受到人们的广泛关注.此类体系的微相分离行为不仅可以通过内部组成来调节,更会受到外部几何限制的影响.迄今为止,针对本体相已开展了大量卓有成效的研究.越来越多的研究者开始借助理论分析与计算机模拟两种手段对嵌段共聚高分子在一维受限薄膜中的微相分离行为进行全面而又深入的研究.在线性两嵌段共聚高分子体系方面,现有的研究工作已涵盖了一维[5-7]、二维[8-10]与三维[11-13]的几何限制情况.然而,对于非线性嵌段共聚高分子受限体系,即便是在一维受限的情况下,其所受到的关注程度也要低得多.最为简单的非线性高分子模型,是指连接于同一点的 3条线性链所组成的星形共聚高分子.Han等[14]通过自洽场 (self consistent field,SCF)理论研究了星形三嵌段共聚高分子薄膜的微相分离行为,并重点关注了对称与非对称相互作用下结构上接近对称的星形高分子所形成的微观形态与薄膜厚度和表面场之间的关系.此外,Romiszowski与Sikorski等[15-17]利用Monte Carlo模拟对星形高分子在一维受限体系中的微观性质进行了全面考察,但却未涉及到嵌段共聚高分子体系.因而,针对星形两嵌段共聚高分子在受限体系中的微相分离行为的研究显得极为迫切.

一般而言,有两种类型的星形两嵌段共聚高分子,分别以 (Ax)n(By)n和 (AxBy)n来表示,结构如图1所示,其中 (Ax)n(By)n是由 n条线性 AxBy共聚高分子链在嵌段连接点处相连而成,而 (AxBy)n则是在其中的一端 (A或 B)相连而成.因此,单个(Ax)n(By)n星形分子共含有 2n条分枝,其中 n条分枝中的每一条由 x个 A单体组成,另外 n条分枝中的每一条由 y个 B单体组成;而单个 (AxBy)n星形分子则总共含有 n条分枝,且每条分枝都对应于一条完整的线性AxBy共聚高分子链.

在跟踪考察高分子体系复杂微观相的动态形成过程中,耗散粒子动力学 (dissipative particle dynamics,DPD)方法发挥了重大作用.本研究利用该方法对(Ax)n(By)n和 (AxBy)n两类星形共聚高分子在薄膜中的微相分离行为进行了计算机模拟研究.

1 模拟方法与模型构造

DPD方法由Hoogerbrugge和Koelman首次提出[18-19],后经他人多次完善[20-21],现已在众多领域得到了成功应用,并被证明是一种研究复杂流体介观尺度行为的有效方法[22-24].DPD体系中的基本单元为代表实际体系分子集团的粗粒化软粒子,其时间演化遵循牛顿运动定律[21].粒子间的相互作用力 fi由 3部分组成,其中每一部分均通过成对加和计算得出,公式如下:

星形两嵌段共聚高分子单体模型完全按照图1所示进行构造.如图2所示,每个星形分子均由与A,B粒子相似的中心粒子 C将 4条线性 AxBy两嵌段自由链按照相应的方式连接于其上而成,其中灰色与黑色粒子分别代表 A,B嵌段,连接中心的空心圆代表 C嵌段.两类星形高分子则可分别表示为(Ax)4(By)4与 (AxBy)4,其中每条线性链由 10个具有相同直径 rc的软粒子组成,即 x+y=10,每一个星形分子中含有 41个粒子.每一条自由链通过键对间的简谐振动弹性力 FSij=Crij,将单个粒子串接而成,其相邻粒子间的初始键长均为单位长度.

图1 星形两嵌段共聚高分子的结构示意图Fig.1 Schematic represen tation of two types of stard iblock copolymer s

图2 两类星形共聚高分子的 DPD模型Fig.2 DPD models of two types of star-d iblock copolymer s

模拟在一大小为 41(x)×41(y)×L(z)的矩形盒子中进行,其中 x和 y方向采用周期性边界条件,而 z方向则设定为相距 L(即膜厚)且不可穿透的边界,每一个靠近边界的粒子均受到排斥力 apb=25.0作用,以使其尽可能远离边界.此外,粒子与 z方向边界发生无能量损失的弹性碰撞之后,将以对称的路径反弹回体系中以防止其“逃逸”,即反弹后的速度在 x,y方向不变向,而在 z方向则完全反向.体系数密度ρ=3.0,对比温度 kBT=1.0.A-A,B-B,A-C与B-C间的排斥力均取为 25.0.A-B间的相互作用能有三种选择:50.0,75.0和 100.0,分别对应弱、中、强排斥体系.膜厚 L在 [6,18]范围内以固定间隔选取.随机力标准差σ=3.67,弹性系数 C=4.0.运动方程采用标准的 velocity-Verlet算法[20]进行积分求解,其步长Δt=0.05.每一轮模拟均运行500 000步以保证达到体系平衡.

2 模拟结果与讨论

2.1 微相分离结构及其相图

在不同A-B相互作用强度下改变 A嵌段的组分分率 fA(计算时未涉及 C嵌段)以及薄膜厚度 L.然后,我们通过 DPD模拟观察到微团状 (M)、岛状(IS)、相连岛状 (CIS)、螺旋状 (HE)、迷宫状 (MA)、层状 (LAM)、平行管状 (PT)以及随机管状 (RT)等一系列介观有序结构,如图3所示 (灰色部分为 A嵌段等密度分布,空白部分代表 B嵌段).相应的描述星形 (Ax)4(By)4与 (AxBy)4两嵌段共聚高分子微相分离行为的相图分别如图4和图5所示,其中“D IS”代表未发生相分离的无序状态,且每一组均包含有弱、中、强排斥 3种情况.显然,与 (AxBy)4相比较,(Ax)4(By)4体系的每一张相图都是完全对称的,这一点与两类星形高分子本身的结构特征相一致,且类似于我们此前研究工作中所发现的它们在本体相中的微相分离行为[25].此外,就结构显著不对称体系而言,(A1)4(B9)4与 (A9)4(B1)4两类体系在中等强度排斥下均形成了有序结构,而此时(A1B9)4与 (A9B1)4却仍处于无序状态,即在相同条件下,(Ax)4(By)4要比 (AxBy)4更容易发生微相分离,这一点同样可以归结为是由两类高分子本身结构的差异所造成.由图2不难发现,(Ax)4(By)4分子中每条分支上的 A,B嵌段是完全分离的,而在(AxBy)4分子中则是完全混合的,因而后者较前者更难发生相分离.这一现象再次与该体系在本体相中的情况相似[25].还有一点值得关注,(AxBy)4体系在 fA=0.2时已出现主要特征为“A嵌段点阵矗立于 B嵌段内”的岛状结构,而 (Ax)4(By)4体系在此组成下则未出现岛状结构.同样根据图2所示,(AxBy)4分子中 A嵌段显然处于“内部”,而 B嵌段则构成“外围”,即其分子结构本身已符合岛状结构的基本特点,而 (Ax)4(By)4的分子结构则不具备此特点.因此,在相同情况下,(AxBy)4比 (Ax)4(By)4更易形成岛状结构.

2.2 影响因素分析

两嵌段共聚高分子体系中所形成的微相分离结构往往取决于两个嵌段组分间的竞争.无论体相还是受限体系,任一组分均希望占据嵌段分隔曲面(界面)的凸面一侧,以便拥有更大的伸展空间.而此竞争的结果则由两个嵌段组分的相对聚合度来决定.如果两个嵌段在体系中所占据的组分分率相等或较为相近,则竞争的结果为平坦界面;若二者相差较大,则会在体系中形成弯曲界面,组分分率较高的嵌段占据凸面一侧,而另一嵌段则占据凹面一侧.因而,就体系组成而言,当 A,B两种嵌段的组分分率fA与 fB相等 (fA=0.5)或相差较小 (fA=0.4,0.6)时,星形共聚高分子薄膜往往形成平行层状或类层状的迷宫状结构;随着 fA与 fB之间差距的逐渐增大,体系将会形成螺旋状、相连岛状、平行 (随机)管状以及微团状等一系列更为多样的微相分离结构.与此前的研究结果[22]进行对比,可以发现,相同组成的星形共聚高分子体系在体相与薄膜中所形成的介观结构之间还存在一定的对应关系.例如,图3(a)所示的微团状结构可对应于体相中形成的体心立方球状结构;图3(b)和图3(d)中所展示的平行管状与岛状两类结构仅在取向上有所不同,但均可对应于体相中形成的六方圆柱结构;图3(f)所示的螺旋状结构可对应于体相中所形成的螺旋状结构.此外,体相与薄膜体系中的层状结构亦可相互对应,而随机管状、相连岛状以及迷宫状等 3类结构则未出现于本体相中.由此可见,一维受限能够在一定程度上使得该体系所形成的微相分离结构更为多样化.

就薄膜厚度而言,厚度越大,模拟体系中的粒子数越多,在相互作用一定的情况下形成微相分离结构的难度就越大,从而在一定程度上降低了有序性.例如,随着 L不断增大,平行管状结构将会退化为随机管状结构;岛状结构先退化为相连岛状结构,进而过渡到螺旋状结构.

就组分间相互作用而言,排斥越强,同一体系中不同嵌段间的分离程度就越大,所形成的微相分离结构则更为规整有序.例如,随着 A-B间排斥作用的逐渐增强,分子结构对称性较强的体系 (fA=0.4～0.6)所形成的迷宫状区域明显缩小,层状区域逐步扩大;分子结构不对称性较强的体系 (fA=0.1～0.3,0.7～0.9)所形成的相连岛状区域明显缩小,岛状区域逐渐扩大;随机管状区域缩小,平行管状区域扩大.

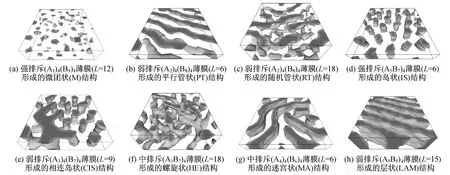
图3 星形两嵌段共聚高分子薄膜的微相分离结构Fig.3 Representative simulated mesoscop ic structure for the star-d iblock copolymer f ilm s

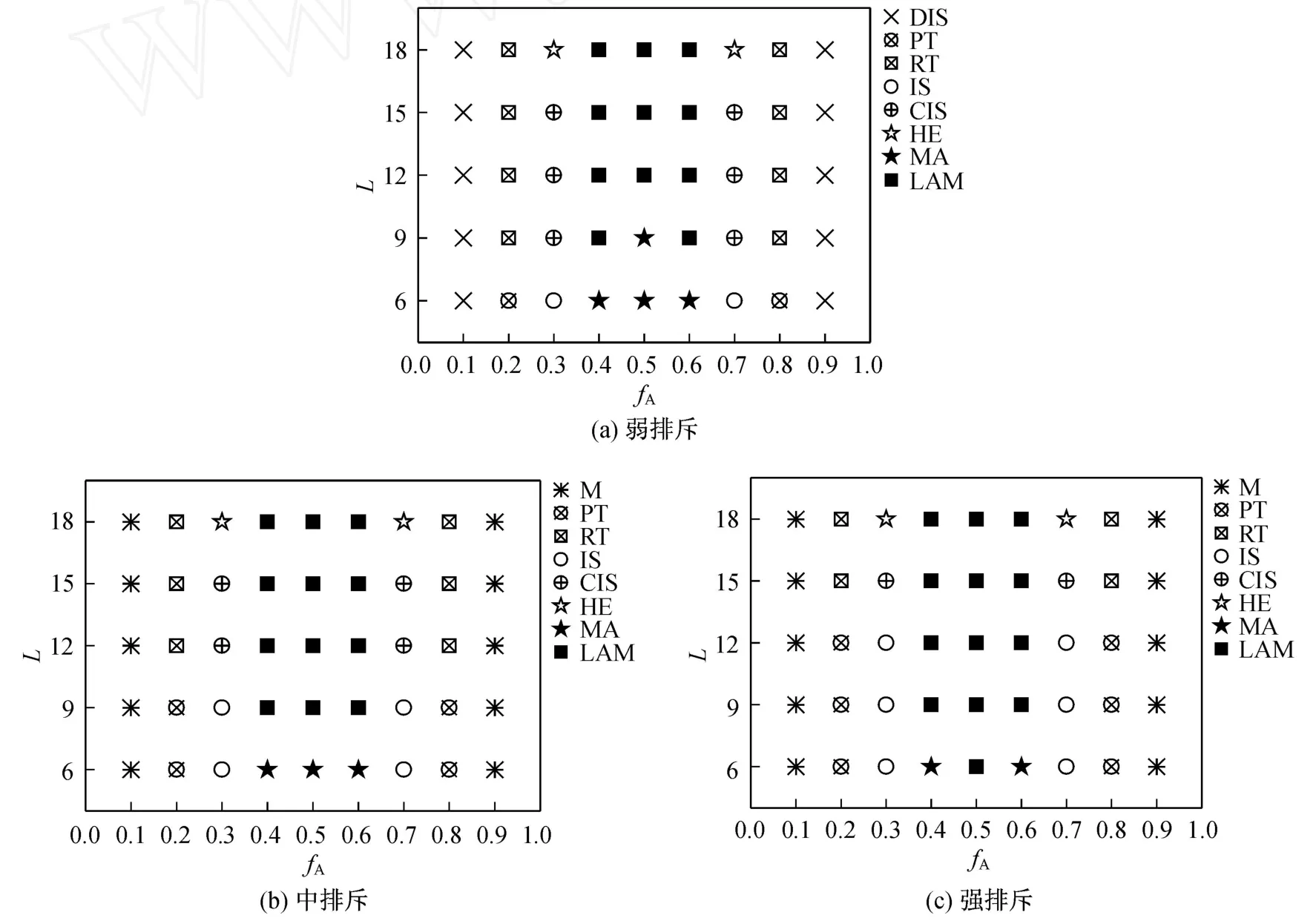
图4 星形(Ax)4(By)4两嵌段共聚高分子分别于弱、中、强排斥作用下的微相分离相图Fig.4 Simulated phase d iagram s for the(Ax)4(By)4star-d iblock copolymer film s in the cases of weak,med ium and strong repulsions,respectively

图5 星形(AxBy)4两嵌段共聚高分子分别于弱、中、强排斥作用下的微相分离相图Fig.5 Sim ulated phase d iagram s for the(AxBy)4star-d iblock copolym er f ilm s in the cases of weak,med ium and strong repulsion s,respectively

3 结 束 语

本工作利用耗散粒子动力学模拟方法研究了(Ax)4(By)4与 (AxBy)4两类典型的星形两嵌段共聚高分子薄膜的微相分离行为,观察到了一系列有序结构,并且获得了相应的相图.研究结果表明:(Ax)4(By)4体系的相图较 (AxBy)4体系具有更明显的对称性,且前者比后者更易发生微相分离,这一点与体相中的情况相类似,而同等条件下后者比前者更易形成岛状结构;组成相同的星形共聚高分子体系在体相与薄膜中所形成的介观结构之间存在着一定的对应关系,且一维受限能够使得该体系所形成的微相分离结构更为多样化;较小的薄膜厚度与较强的A-B组分间排斥作用均有利于增强所形成结构的有序性.

[1] BATES F S,FREDERICKSON G H.Block copolymer thermodynamics-theory and experiment[J].Annual Review of Physical Chemistry,1990,41:525-557.

[2] CORBERI F,GONNELLA G,LAMURA A.Two-scale competition in phase separationwith shear[J].Physical Review Letters,1999,83(20):4057-4060.

[3] LOPESW A,JAEGER H M.Hierarchical self-assembly of metal nanostructures on diblock copolymer scaffolds[J].Nature,2001,414(6865):735-738.

[4] TURN-ALBRECHT T,SCHOTTER J,KAESTLE G A,et al.Ultrahigh-density nanowire arrays grown in selfassembled diblock copolymer templates[J].Science,2000,290(5499):2126-2129.

[5] ANGERMAN H J,JOHNER A,SEMENOV A N.M icrophase separation in thin block copolymer films:a weak segregation mean-field approach [J].Macromolecules,2006,39(18):6210-6220.

[6] FENG J,L IU H L,HU Y.M icrodomain morphology of symmetrical diblock copolymer thin films confined in a slit[J]. Macromolecular Theory and Simulations,2002,11(5):549-555.

[7] FENG J,L IU H L,HU Y.Asymmetric diblock copolymer thin film confined in a slit:microphase separation and morphology[J].Macromolecular Theoryand Simulations,2002,11(5):556-565.

[8] FENG J,L IU H L,HU Y.Mesophase separation of diblock copolymer confined in a cylindrical tube studied by dissipative particle dynamics[J].Macromolecular Theory and Simulations,2006,15(9):674-685.

[9] XIAO X Q,HUANG YM,L IU H L,et al.Morphology transition of block copolymers under curved confinement[J].Macromolecular Theory and Simulations,2007,16(8):732-741.

[10] HECKMANN M,DROSSEL B.Cylindrical phase of block copolymers in thin films[J].Macromolecules,2008,41(20):7679-7686.

[11] HE X H,SONGM,L IANG H J,et al.Self-assembly of the symmetric diblock copolymer in a confined state:Monte Carlo simulation [J]. Journal of Chemical Physics,2001,114(23):10510-10513.

[12] FRAA IJE J G EM,SEV INK G J A.Model for pattern formation in polymer surfactant nanodroplets[J].Macromolecules,2003,36(21):7891-7893.

[13] FENG J,L IU H L,HU Y.M icro-phase separation of diblock copolymer in a nanosphere:dissipative particle dynamics approach[J].Fluid Phase Equilibria,2007,261(1/2):50-57.

[14] HAN W C,TANG P,L IX,et al.Self-assembly of star ABC triblock copolymer thin films:self-consistent field theory[J].Journal of Physical Chemistry B,2008,112(44):13738-13748.

[15] ROM ISZOWSKI P,SIKORSKIA.Monte Carlo simulations of star-branched polymers confined between two walls[J].Journal of Chemical Physics,2002,116(4):1731-1736.

[16] SIKORSKIA,ROM ISZOWSKI P.Properties of branched confined polymers[J].Journal of Chemical Physics,2004,120(15):7206-7211.

[17] ROM ISZOWSKI P,SIKORSKIA.Star-branched polymers in an adsorbing slit:a Monte Carlo simulation[J].Journal of Chemical Physics,2005,123(10):104905.

[18] HOOGERBRUGGE PJ,KOELMAN JM V A.Simulating microscop ic hydrodynamic phenomena w ith dissipative particle dynamics[J].Europhysics Letters,1992,19(3):155-160.

[19] KOELMAN J M V A,HOOGERBRUGGE P J.Dynamic simulations of hard-sphere suspensions under steady shear[J]. Europhysics Letters,1993,21(3):363-368.

[20] ESPAÑOL P,WARREN P B.Statistical mechanics of dissipative particle dynamics[J].Europhysics Letters,1995,30(4):191-196.

[21] GROOT R D,WARREN P B.Dissipative particle dynamics: bridging the gap between atomistic and mesoscopic simulation [J]. Journal of Chemical Physics,1997,107(11):4423-4435.

[22] GROOT R D,MADDEN T J.Dynamic simulation of diblock copolymermicrophase separation[J].Journal of Chemical Physics,1998,108(20):8713-8724.

[23] GROOT R D,MADDEN T J,TILDESLEY D J.On the role of hydrodynamic interactions in block copolymer microphase separation [J]. Journal of Chemical Physics,1999,110(19):9739-9749.

[24] YUAN SL,CA IZ T,XU G Y.Mesoscopic simulation of aggregates in surfactant/oil/water systems[J].Chinese Journal of Chemistry,2003,21(2):112-116.

[25] XU Y,FENG J,L IU H L,et al.M icrophase separation of star-diblock copolymer melts studied by dissipative particle dynamics simulation[J].Molecular Simulation,2006,32(5):375-383.

(编辑:赵 宇 )

M icrophase Separation of Star-D iblock Copolymer Film s by D issipative Par ticle Dynam ics Simulation

XU Yi1, FENGJian2
(1.School of Environmental and Chemical Engineering,Shanghai University,Shanghai200444,China;2.Department of Chemistry and Life Science,Chuzhou University,Chuzhou 239012,Anhui,China)

O 242.1

A

1007-2861(2010)05-0476-06

10.3969/j.issn.1007-2861.2010.05.006

2010-06-08

上海市重点学科建设资助项目(S30109);上海高校选拔培养优秀青年教师科研专项基金资助项目(SHU07013);上海大学科学技术发展基金资助项目(A10011107901);上海大学创新基金资助项目(A 10011108008)

徐 毅 (1980～),男,讲师,博士,研究方向为分子模拟.E-mail:tree2000xy@shu.edu.cn