“凸”字形单调多边形三角剖分算法的研究

刘 燕

（赤峰学院 计算机科学与技术系，内蒙古 赤峰 024000）

“凸”字形单调多边形三角剖分算法的研究

刘 燕

（赤峰学院 计算机科学与技术系，内蒙古 赤峰 024000）

单调多边形的三角剖分是计算几何的一个重要分支，其中严格单调多边形的三角剖分已有了线性时间算法，但该算法对于一般单调多边形还不能给出正确的剖分.本文对严格单调多边形三角剖分算法进行了详细分析，给出了一般单调多边形的三角剖分算法.

对角线；单调多边形；三角剖分

1 引言

计算几何研究的任务是如何处理通过各种途径获得的几何信息，给出最优的处理几何信息的方法.而多边形正是许多真实物体外形的一种既方便又精确的描述工具，并且在计算上很容易实现.它的应用包括自动符号识别中单个符号的形状，机器人运动时要避免的障碍物的形状等.但是通常多边形又是相当复杂的，因此经常需要将它们看成是由简单的部分组成，这就是划分多边形的问题.例如对真实图像进行抽象和二值化后，再进行三角剖分，通过和标准图像的匹配，用于外观检测和筛选等[1].可见多边形的三角剖分是计算几何的一个重要分支，随着计算机在图形图像处理方面的广泛应用，对多边形的三角剖分及其对偶图的研究与应用，越来越受到重视.

2 简单多边形三角剖分的重要概念[2]

简单多边形：设平面上n个点p1,p2,…,pn按循环排序方法逆时针排列，p1在pn之后，有设e1=p1p2,e2=p2p3,…,en=pnp1是连接各点的n条线段，则这些线段界限一个多边形，并且满足：

①循环排序中相邻线段对的交点是两者之间的公共单顶点：ei∩ei+1=pi+1；

②不相邻的线段不相交，ei∩ej=覫，j≠i+1；i=1,2,…,n；en+1=e1，pn+1=p1.

（2）链：是一条折线，记作：L=，其中 p={p1,p2,…,i=1,2,…}是顶点集，e={e1,e2,…,i=1,2,…}是边集.

（3）单调：若对于任一正交于链L的直线L'，有L'交L是空集或是一个点，或是一段线段，即至多只交于一个连通的部分，称链L关于直线L`是单调的.如果L'与L只交于一点或不交，则称链L关于直线L`为严格单调.

（4）对角线：P 是多边形，pi、pj∈P，若 pipj∈P，则称pi、pj彼此可视的.若pipj与多边形的边界只交于两个顶点，则称pi、pj是清晰可视的.清晰可视的两顶点之间的线段，称为多边形的对角线.

（5）凸顶点：对于多边形任意三个连续的顶点pi,pi+1,pi+2,若pipi+2是对角线，则角pi+1称为凸角，顶点pi+1称为凸顶点.

（6）三角剖分：多边形三角剖分是指：对于任意简单的多边形，连接其所有的对角线，将多边形划分为若干个三角形平铺的集合.

3 简单多边形的三角剖算法分析

简单多边形的三角剖分方法一般是先经过修剪歧点[2]，将其变为严格单调多边形，再按Y坐标由低到高划分为左右两条严格单调的链Ll与Lr，进而对严格单调多边形进行三角剖分，严格单调多边形三角剖分的算法概要在文献[3]、[4]中有详细的叙述，算法的基本特点为：

（1）p不在凹链上，以p为基点将凹链中的点由下向上去掉三角形，直到p进入凹链为止.

（2）p在凹链上，以p为基点将凹链中的点由上向下去掉三角形，直到p进入凹链为止.

（3）对于当前处理的顶点p，当无对角线输出时，才进入凹链，可见凹链中的顶点除头顶点以外，必然属于同一条多边形的分支链，且是凹的或平的.

为了讨论问题方便起见，本文所用的坐标系为水平向右为x轴，竖直向下为y轴.将上述算法应用于下面的图1，如果在list中，y值相同的顶点，右链处于优先的位置，即list={p1,p3,p4,p2,…}，输出对角线为dlist={p4p1,p4p2,…}，可以给出正确的三角剖分；如果左链处于优先的位置，即list={p1,p2,p3,p4,…}；则输出对 dlist={p3p2,p4p2, …}，由于 p2、p3、p4三点在同一水平线上，则p2p3不是正确的对角线.可见此时不会给出正确的三角剖分.

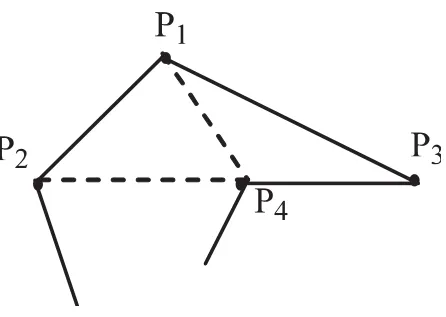
图1

对于图2而，如果在list中，y值相同的顶点，左链处于优先的位置，即list={p1,p2,p3,p4,p5,p6,…}，凹链中顶点为vchain={p1,p2,p3,p4}，p=p5时 ，按原算法依此输出对角线为 dlist= {p5p2,p5p3,p5p4,…}，显然由于 p2、p5不在同一条水平线上，p5p2是正确的对角线，p3、p5虽然共线，但却是左右两链中所有同一条水平线上离的最近的点，因而也是正确的对角线，p4、p5也是水平共线的两点，但由于中间有点p3，因而p5p4不是正确的对角线.可见此时也不会给出正确的三角剖分.如果在list中，y值相同的顶点，右链处于优先的位置，则先输出对角线p5p2后，就与图1相似了，同样不会给出正确的三角剖分.

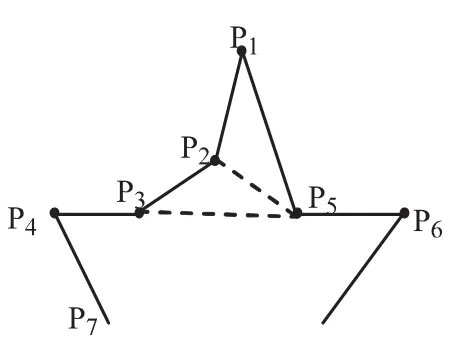
图2

图3和图1的情况也相似，右链优先时可以给出正确的三角剖分，左链优先时不会给出正确的三角剖分.出现错误的原因是上述三个多边形不是严格单调的，它们在水平方向上有多个点共线，构成一个连通的区域，使得由原算法输出的对角线与多边形的边重和，不符合计算几何中对角线的定义.由此得出如下两点结论：

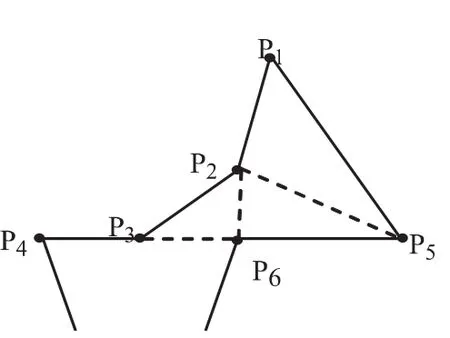
图3

（1）上述算法不适用一般单调多边形的三角剖分，问题均出在p不在凹链上的情况下.

（2）单调多边形的三角剖分算法的正确与否和多边形顶点进入list链中时,左、右两链中y值相同的顶点谁优先有关.

在下面分析一般单调多边形的三角剖分算法时，约定在list中，y值相同的顶点，以左链优先.根据原算法思想，如果p在凹链vchain上，则无须判断沿x轴方向顶点有无共线，若x（凹链中的尾顶点）是严格凸顶点的，连p和凹链的倒数第二个顶点，去掉三角形；否则p进凹链.原算法在这一部分不用做改动.下面重点讨论p不在凹链上的情况.

对图2而言，当p=p5不在凹链上，按原算法输出对角线 p5p2，p5p3以后，凹链中顶点集为vchain={p3,p4}，由于 p3、p4、p5 在水平方向共线，p3在中间，按愿算法输出的对角线p4p5是不正确的.可见，当p不在凹链上时，算法必须先判断p与凹链中的第二个顶点是否沿水平方向共线，若不共线，则可按原算法输出对角线；否则必须对共线的顶点做特殊处理后才能输出正确的对角线.

对图3而言，当p=p5不在凹链上，按原算法输出对角线p5p2，凹链中顶点集为vchain={p2,p3,p4}，若原算法还应输出对角线 p5p3，p5p4，由于 p3、p4、p5、p6在水平方向共线，p3、p6在中间，显然按愿算法输出的对角线p5p3、p5p4是不正确的.同样必须对共线的顶点做特殊处理后才能输出正确的对角线.本文解决上述问题的方法如下：

（1）由于在list中，y值相同的顶点，以左链优先，所以当凹链属左链时（以凹链中尾顶点原属的链为准），当前待处理的顶点p不在凹链上，才会出现图2、图3的情况；此时能否正确输出对角线，要看顶点p、w（凹链中的第二个顶点）和s(p在list中的后继)三者间的位置关系.当凹链属右链时，当前待处理的顶点p不在凹链上，那么p是左链上的顶点，它必然在凹链以下，原算法不会输出错误的对角线.

（2）由于处于同一水平线上的点分别属于不同的单调链，当凹链属左链而顶点p为右链时，只有分属于两个链中且离的最近的两点之间才有一条正确的对角线，而其他点的对角线，要么是和水平线以上的点相连，即和凹链中的头顶点相连；要么是和水平线以下的点相连，这些点仍在list链中.

（3）当凹链中的所有点都处于同一水平线上时，由于简单多边形的特点，这些点不能沿x轴往复分布，只能沿某一方向分布，所以，必须将就这些点重新沿x轴方向排序.

（4）当凹链中的点处于同一水平线且分别属于不同的单调链时，对于后续处理的某个顶点p而言，它必然有时在凹链上，有时又不在凹链上，即有时要删除凹链的头顶点，有时又要删除凹链的尾顶点，这将会导致错误.为此，在对凹链中的共线点排序的同时，还必须把所有的点改为和p点处于同一链中.

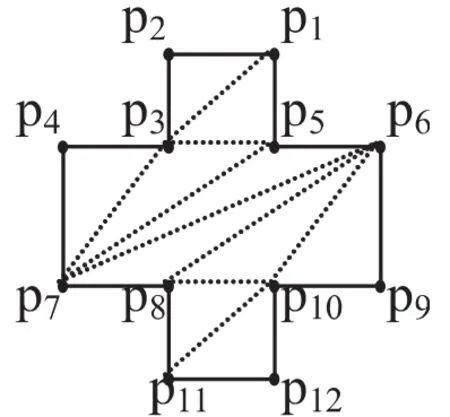
将上述四点应用于图2，当p=p5时，删除头顶点p1后，由于p6.x>p5.x，此时因为p3、p5之间有正确对角线，可输出对角线p5p3并删除头顶点p2，此时凹链vchain={p3,p4,}已变成平的，然后将凹链沿x轴排序，并改变顶点所属的链，这样将导致p5、p6依此进入凹链中，凹链vchain={p3,p4,p5,p6}，当p=p7时，再输出对角线{p7p3,p7p5,p7p6}.对于图3，当p=p5时，由于p5.x

4 一般单调多边形的三角剖分算法

约定：h：vchain中的头顶点；p当前待处理的顶点；s：p 在 list中的后继；x：vchain 中的尾顶点；w：vchain中的第二个顶点或倒数第二个顶点；flag：顶点的链属性，L表示左链，R表示右链；

输入：单调多边形的两条链Ll、Lr；沿y轴将左、右两链的顶点合并为顶点表vlist，并约定当两链中的顶点y坐标相同时，以左链优先.

输出：对角线表dlist；

由于当p点在凹链时，原算法不需要修改，下面仅给出p不在凹链上的部分算法：[1、顶点排序]

沿y轴将左、右两链的顶点合并为顶点表vlist，并约定当两链中的顶点y坐标相同时，以左链优先.

[3.3重复剖分]若p不是vlist中的最小顶点或凹链中有两个以上顶点，做3.1或3.2；否则算法结束.

运用上述算法对图4进行剖分如下：

左链L={p2,p3,p4,p7,p8,p11}；右链 R={p1,p5,p6,p9,p10,p12}；

vlist={p2,p1,p3,p4,p5,p6,p7,p8,p9,p10,p11,p12}；

dlist={p3p1,p5p3,p7p3,p7p5,p7p6,p8p6,p10p6,p10p8,p11p10}；

图4

5 算法的时间复杂性分析

该算法和原算法相比更加通用，更加高效，且易于实现.对所有顶点排序，时间复杂性[5]可达o(n)；初始化时间复杂性可达o(1)，剖分时，每个顶点进出凹链最多为一次，所以时间复杂性最多为o(n)，如有同一水平线上的顶需排序，时间复杂性可达o(n).所以总的时间复杂性上界为o(n)，下界为o(n2).本算法已在V.B6.0上实现.

〔1〕杨平，林意.一种三角剖分算法实现图形的匹配.计算机工程与应用，2003（8）.

〔2〕Zhou Peide，An algorithm for partitioning polygons into convex parts.Journal Beijing Institute of Technology,1997,6(4):363-368.

〔3〕周培德.计算几何—算法分析与设计.清华大学出版社，2000.

〔4〕廖士中.计算几何讲义.辽宁师范大学，1999.

〔5〕严蔚敏.数据结构.清华大学出版社，1996.

TP393

A

1673-260X（2010）01-0025-03

内蒙古自治区高等院校科研项目基金资助（NJzy08153）