基于的支撑架特征值屈曲分析

屠凤莲，范顺成，罗文龙

（1.河北工业大学 机械学院，天津 300130；2.中国建筑科学研究院 建筑机械化研究分院，河北 廊坊 065000）

随着科学与经济的发展，刚架结构被广泛应用于机械工程和建筑工程中，它们的安全与稳定问题备受关注，尤其对于承载重量的细长类刚架，为保证结构甚至生命财产的安全，必须要弄清承重刚架正常工作的载荷范围和失效机理，这就有必要去计算其发生塑性弯曲变形时的最小临界载荷[1,2,3].其计算可以采用大型有限元分析软件ANSYS来完成，ANSYS软件是集结构、流体、电场、磁场、声场、热分析于一体的大型通用有限元分析软件，它是由美国ANSYS公司开发的，能够与多种先进的CAD软件共享数据，如AutoCAD、Pro/Engineer、SolidWorks、NASTRAN、Alogor、I-DEAS等，是现代产品设计中的高级CAD软件之一.对结构的屈曲分析ANSYS提供了两种方法，包括非线性屈曲分析和特征值屈曲分析（线性屈曲分析）.本文利用ANSYS软件对建筑施工中某承重系统的一个支撑架进行了有限元建模和特征值屈曲分析，并利用ANSYS的后处理模块观察了它的各阶屈曲模态及其轴向应力.

1 特征值屈曲分析的原理及ANSYS软件的分析步骤

1.1 特征值屈曲分析的原理

分析结构的稳定性时，在基于线弹性的特征值屈曲响应分析中，结构屈曲的临界载荷可以表示为

线性屈曲有限元计算的实质就是计算整体结构在线性刚度基础上加上初始应力刚度影响后结构屈曲的最小临界载荷.另外，从公式 ( 1)中看出：为了得到正确的值，作用载荷的数值可以是任意的.例如：如果增大到原来的10倍，用方程 (2)求解的屈曲特征值就会缩小到原来的1/10，也就是说它们的乘积保持不变.因此利用ANSYS软件计算结构的特征值屈曲解时，只需施加单位载荷的外力即可.对特征值的求解问题，ANSYS软件提供了 S ubspace（子空间法）和 B lock Lanczos（兰索斯分块法）两种求解方法.

虽然特征值屈曲分析方法未考虑结构非线性和初始缺陷的影响，而只适用于较理想的结构，但由于该方法计算简单，并且是非线性屈曲分析计算结果的上限，因此目前仍被广泛采用.

1.2 ANSYS软件的分析步骤[4-5]

ANSYS软件对结构进行特征值屈曲分析的步骤如下.

1.2.1 前处理

在前处理模块中创建有限元模型，即进行参数定义、实体建模和网格划分.该过程与其他分析类型类似，但应注意：特征值屈曲分析只允许线性行为，如果定义了非线性单元，则按线性处理；必须定义材料的弹性模量或者某种形式的刚度.

1.2.2 获得静力解

对已建立的模型施加载荷与边界条件，并进行有限元计算.该过程与一般的静力分析类似，但需注意几点：1）必须激活预应力影响；2）通常只需施加一单位载荷即可，不过ANSYS允许的最大特征值是1000000，若求解时特征值超过了这个限度，则需施加一较大载荷.当施加单位载荷时，求解得到的特征值就表示屈曲临界载荷，当施加非单位载荷时，求解得到的特征值乘以施加的载荷就得到屈曲临界载荷；3）特征值相当于所施加载荷的放大倍数，因此也称载荷因子；4）可以施加非零约束作为静载荷来模拟预应力；5）在求解完成后必须退出求解器.

1.2.3 获得特征值屈曲解

详细步骤为：进入求解器 指定分析类型 指定分析选项 指定载荷步选项 保存结果 开始求解

退出求解器.在分析选项步骤中选择特征值求解方法（Subspace或Block Lanczos），并输入所要提取的特征值阶数.

1.2.4 扩展解

无论采用哪种特征值求解方法，如果想得到屈曲模态的形状，就必须执行扩展解.详细步骤为：进入求解器 指定为扩展求解 指定扩展求解选项 指定载荷步选项 数据库和结果文件输出 扩展求解退出求解器.在扩展求解选项中指定扩展模态的阶数，并指定是否需要进行应力计算.

1.2.5 后处理

详细步骤为：进入后处理器 列出所有屈曲特征值 读取指定模态 显示屈曲模态形状 显示相对应力分布云图.

2 建立支撑架有限元模型

2.1 实体模型描述

该支撑架在承重系统中的最大承载为5kN，它全部由空心钢管焊接而成，管外径25mm，壁厚2mm，其总高15m，分成15小节，每小节1m，支撑架横截面为边长200mm的正方形，如图1所示.每小节之间的横向加强筋是空心管端部砸扁后与4根竖管焊接的.该结构底部固支，顶部四角顶点受均匀集中载荷作用.

2.2 建立有限元模型

为简化有限元模型，应对实体模型进行适当简化，忽略横向加强筋两端的砸扁对结构刚度产生的影响，假设所有焊接接头都为完全焊接.进入Ansys的前处理器，首先定义单元类型：选择Beam4梁单元对支撑架进行有限元分析，该单元是一种可用于承受拉、压、弯、扭的单轴受力单元，在每个节点上有6个自由度，并且它具有应力强化和大变形能力；然后根据已知条件定义单元的实常数：单元的横截面积惯性矩，单元厚度；最后定义材料性质：选择线性各向同性材料，输入弹性模量，泊松比

由于该支撑架结构并不复杂，采用自底向上建模法.在当前激活的坐标系内先定义4个关键点，再由关键点生成线、面，然后由面拉伸成体，再删除面和体，指定网格划分尺寸，最后通过复制生成结构整体模型，按照指定的尺寸划分网格，从而生成有限元整体模型，如图2所示，该模型共1 396个节点，1 456个单元.

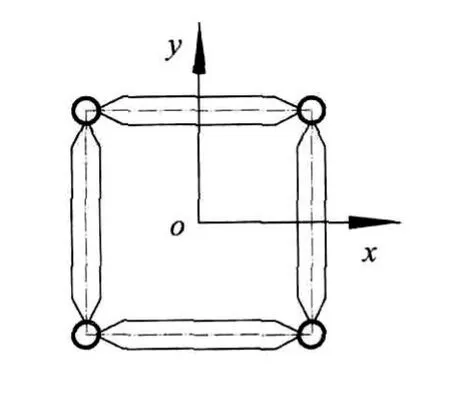
图1 支撑架横截面示意图Fig.1 Sketch draw ing of thebearer frame's crosssection

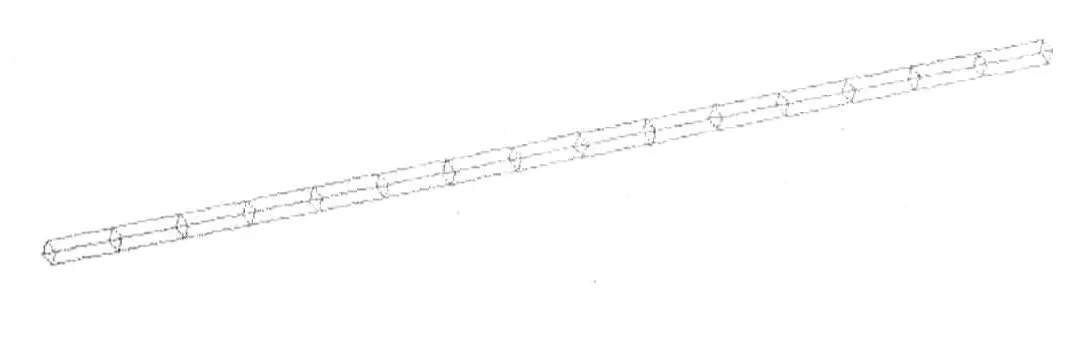
图2 支撑架有限元模型Fig.2 The finiteelementmodelof thebearer frame

3 支撑架特征值屈曲分析[6,7]

首先对已建立的有限元模型定义边界条件和施加外载荷：将支撑架底部的4个顶角的节点限制所有自由度；对支撑架顶部的4个顶角的节点在竖直方向施加单位载荷，然后进行有限元静力求解.得到静力解后，采用Block Lanczos方法计算结构的前8阶屈曲特征值及相应的轴向应力，并对所求解进行扩展.

屈曲扩展求解的结果被写入结构的结果文件，包括屈曲特征值、屈曲模态形状和相对应力分布，进入通用后处理器可以观察到这些结果.把得到的各阶特征值乘以所施加的载荷，即得到整体结构屈曲的各阶临界载荷；再定义单元表格计算梁的轴向应力，计算结果见表1.

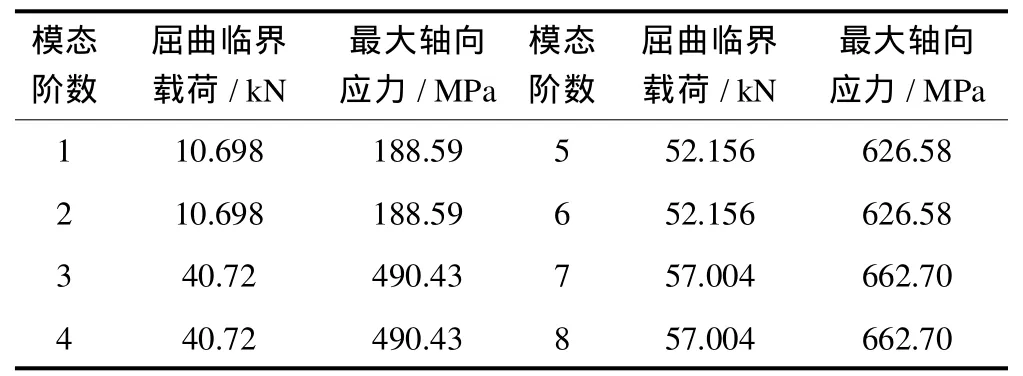
表1 前8阶屈曲临界载荷和最大轴向应力Tab.1 Firsteightbuckling loads and maximum axialstress

从表1中看出：1）支撑架屈曲的最小临界载荷为10.698 kN，远大于该结构的最大承载5 kN，因此该结构在正常的额定载荷内是非常安全的，不会发生屈曲；2）该结构的临界载荷及最大轴向应力第1、2阶相等；第3、4阶相等；依次类推，这是因为该支撑架结构的横截面是正方形，两个方向的主惯性矩相等，因此只需考虑奇数阶屈曲解；3）屈曲临界载荷和最大轴向应力在前8阶随着屈曲阶数的增加而增加.

读入奇数阶屈曲模态的数据，并显示屈曲模态的图形，如图3所示.

图3 支撑架前8阶屈曲模态Fig.3 Firsteightbucklingmodesof thebearer frame

但对承重支撑架来说，最为关注的还是第1阶屈曲模态形状及其相关参数，如图4所示为支撑架的第1阶轴向应力云图.从图中看出，最大模态位移为1m，发生在支撑架顶部，结合轴向应力的单元列表可以知道结构的最大拉应力发生在支撑架根部第96单元，最大压应力发生在支撑架根部第53单元.

4 结构尺寸对屈曲临界载荷的影响

在支撑架的设计中，不同结构尺寸具有不同的屈曲临界载荷，把以上计算结果作为基础，下面研究结构的横向加强筋个数、横截面边长及管的外径对屈曲最小临界载荷及结构稳定性的影响规律.

4.1 横向加强筋个数对屈曲临界载荷的影响

在上述支撑架有限元模型的基础上，只改变横向加强筋的个数，即改变了每小节的长度和总节数，按照ANSYS的分析步骤分别对结构进行屈曲响应计算，得到表2所示的计算结果.

从表2中可以看出，横向加强筋个数对结构的抗弯刚度影响很大，用曲线描绘表中数据，并运用立方差值法对曲线进行光滑处理，即得到横向加强筋个数对结构屈曲的最小临界载荷及最大轴向应力的影响规律，如图5所示.图中曲线表示：结构屈曲的最小临界载荷和最大轴向应力随着横向加强筋个数的增加而增大，因此增加横向加强筋个数能够改善整体结构的刚度.而随着结构刚度的增强，它所承受的最大轴向应力也增大了，所以必须全面考虑结构的刚度和强度.

图4 支撑架第1阶轴向应力云图Fig.4 Theaxialstressdiagram of the first buckling of thebearer frame

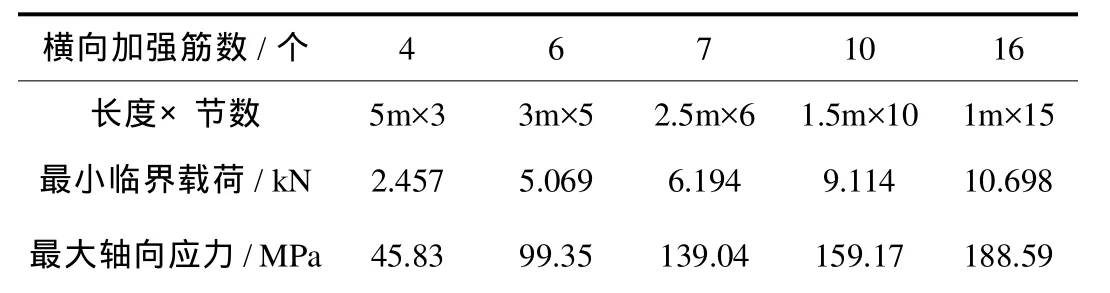
表2 横向加强筋个数对最小临界载荷及轴向应力的影响Tab.2 The influence of transverse-pipe number to buckling load and axialstress

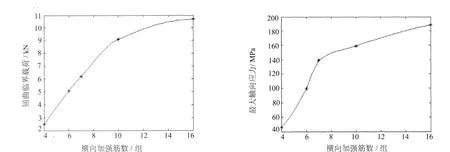
图5 横向加强筋对最小临界载荷及最大轴向应力的影响Tab.5 The influence of transverse-pipenumber to buckling load and axialstress

4.2 横截面边长和管的外径对屈曲临界载荷的影响

在上述支撑架有限元模型的基础上，分别改变横截面边长及管的外径尺寸，按照ANSYS的分析步骤分别对结构进行屈曲响应计算，得到如表3和表4所示的计算结果.

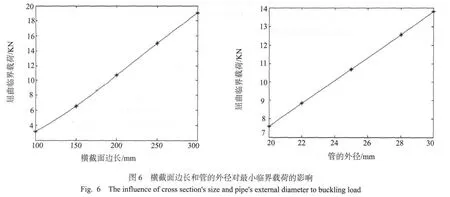
从表3和表4中可以看出，横截面边长和管的外径对结构的抗弯刚度影响很大，用曲线描绘表中数据，并运用立方差值法对曲线进行光滑处理，即得到横截面边长和管的外径对结构屈曲的最小临界载荷的影响规律，如图6所示.图中曲线表示：结构屈曲的最小临界载荷随着横截面边长或管外径的增大而增大.但不能为了提高屈曲载荷（即增大结构的抗弯刚度），就无所顾忌的增大横截面边长和管的外径，实际上当它们增大到一定范围时，结构本身的强度就很差了，因此在进行结构设计时，必须综合考虑结构的刚度和强度.

表3 横截面边长对最小临界载荷的影响Tab.3 The influenceof cross section'ssize to buckling load

表4 管的外径对屈曲临界载荷的影响Tab.4 The influence of pipe'sexternal diameter to buckling load

5 结论

利用ANSYS软件建立了支撑架的三维有限元模型，并对其进行了特征值屈曲分析，证明了该支撑架在额定载荷范围内不会发生屈曲现象；通过计算得到了结构前8阶屈曲变形的临界载荷、各阶屈曲模态及其轴向应力；并进一步分析了支撑架的横向加强筋个数、横截面边长及管的外径尺寸对结构屈曲临界载荷的影响规律.这对支撑架在实际工程中的应用具有一定的指导意义，也为结构的改进和优化设计奠定了理论基础.

[1]陈骥.钢结构稳定理论与设计 [M].第四版.北京：科学出版社，2008.

[2]Kaveh，Salimbahram i.Buckling Load of Symmetric Plane FramesUsing Canonical Forms[J].Computersamp;Structures，2007（2）：1420-1430.

[3]Nuno Silvestre，Dinar Camotim.Elastic Buckling and Second-Order Behaviour of Pitched Roof Steel Frames[J].Journalof Constructional Steel Research，2007（63）：804-818.

[4]段进，倪栋，王国业.ANSYS 10.0结构分析从入门到精通 [M].北京：兵器工业出版社，2006.

[5]尚小江，邱峰，赵海峰，等.ANSYS结构有限元高级分析方法与范例应用 [M].北京：中国水利水电出版社，2006.

[6]黄宇锋，梁尚明，闫喜江，等.基于ANSYS的ITER重力支撑系统特征值屈曲分析 [J].机械设计与制造，2009，1（1）：74-76.

[7]沈春根，王贵成，王树林.HSK工具系统的屈曲响应计算和分析 [J].机械设计与研究，2009，1（1）：77-80.