沥青混合料劈裂回弹模量的研究

罗作芬，郑传超

（1.长安大学 公路学院，陕西 西安 710064；2.西南科技大学 土木工程与建筑学院，四川 绵阳 621010）

沥青路面结构设计中会涉及到沥青混合料弹性模量这一参数的取值问题，现行规范中采用沥青混合料抗压回弹模量，且要求按此模量计算得出的层底拉应力应小于或等于容许拉应力，而该容许拉应力则是通过沥青混合料劈裂试验测得的劈裂强度除以抗拉强度结构系数而得[1]，所以抗压回弹模量与劈裂强度这两个参数的选取就存在不对应关系．这是当前沥青路面设计规范中的一个不足之处，需进行适当修改或完善．

事实上在不同受力方式的试验方法中沥青混合料具有不同的弹性模量值，且各种情况下的模量值具有较大的差距．为了能与路面结构设计指标相对应，使路面结构设计更为完善，沥青混合料弹性模量参数应选取劈裂弹性模量．但目前对沥青混合料在劈裂受力方式下的弹性模量研究较少，主要是因为没有现成的弹性模量计算公式，所以本文针对这一问题利用有限元程序对马歇尔试件的劈裂受力模式进行数值模拟，以拟合出弹性模量计算公式；同时根据劈裂试验数据计算出沥青混合料的弹性模量值；最后对三种受力方式下的弹性模量及其对路面结构受力的影响进行对比分析．

1 数值模拟

1.1 模型的建立

计算时模型采用标准马歇尔试件,直径为101.6±0.25 mm,高度为63.5±1.3 mm，且荷载施加处垫上宽度为12.7 mm、内测曲率半径为50.8 mm的劈裂条，具体结构尺寸见图1．

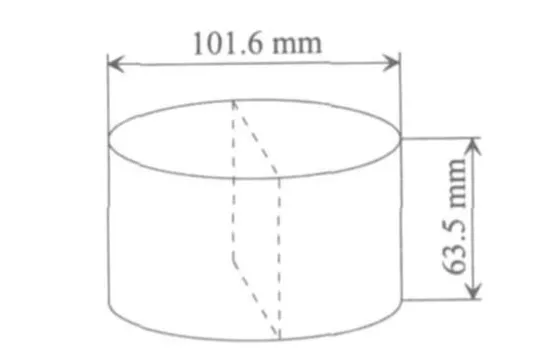
图1 试件结构尺寸示意图Fig.1 Structureand sizefor specimen

使用ANSYS建立二维平面应变模型时，考虑到试件形状的不规则性，模型采用等参8节点平面单元．由于模型的对称性,取试件的1/4建模,竖直面约束X方向上的位移，水平面约束Y方向上的位移；在模型顶部劈裂条宽度范围内施加均布应力p．具体有限元模型见图2所示．

图2 有限元分析模型Fig.2 Model for FEM analysis

1.2 有限元分析

在模拟马歇尔试件劈裂试验时，假定沥青混合料试件结构完全弹性，分析施加荷载应力及施荷处相应位移变形与弹性模量之间的关系，从而找出这3个参数之间的关系式，因此在分析时要变动施加荷载应力与材料参数（弹性模量）这两个参数的取值．然而在假定材料处于完全弹性时，施加应力与相应施荷处的位移是成线性关系的，所以分析时只需要变动材料参数（弹性模量）的取值范围，施加荷载应力固定一个值即可．考虑到沥青材料弹性模量的实际取值范围，本文分析中将沥青混合料参数变动范围取为500～7 500 MPa，且变化幅度为300 MPa．限于篇幅有限元分析过程这里省略．

1.3 分析结果及数据拟合

有限元分析结果具体见表1所示．

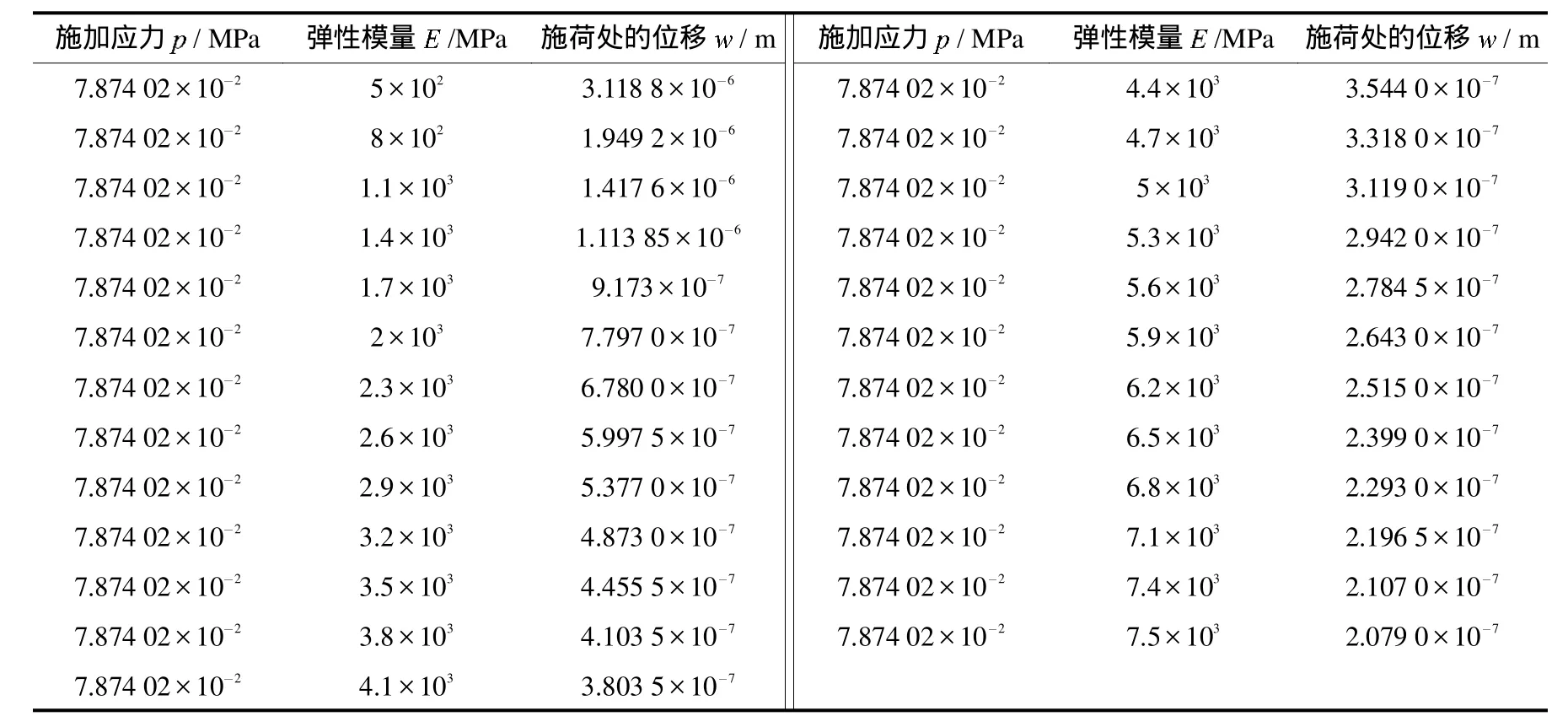
表1 有限元分析结果表Tab.1 The results for FEM analysis

将表1中数据进行初步处理，并用拟合程序1stOpt进行数据拟合，得出

三参数之间的关系式

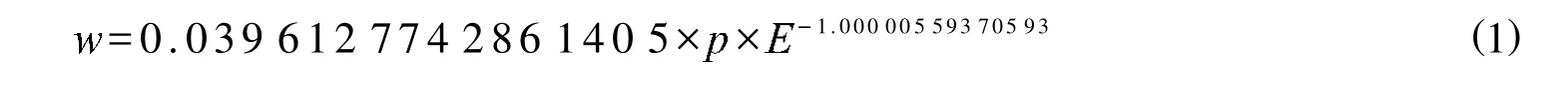
由于关系式中系数较为复杂，会给计算带来不便，所以对系数进行简化得到如下的简化公式

按照简化公式计算出的位移值与源数据之间的误差不超过1%，完全满足精度要求，所以可以用该简化公式来代表三参数之间的关系．由于假定材料为完全线弹性均匀体，所以公式中的位移就等同于回弹变形，因而根据公式 (2)即可推出沥青混合料弹性模量计算公式

2 试验过程及数据采集

2.1 原材料性能

试验中试件所用材料为 AC-13型沥青混凝土，沥青为克拉玛依110#沥青；集料采用玄武岩；为加强沥青和集料的粘附性，在沥青中加入0.2%的抗剥落剂．沥青及混合料的物理性能指标见表2及表3所示．

表2 沥青性能参数Tab.2 Property parametersof asphalt binder

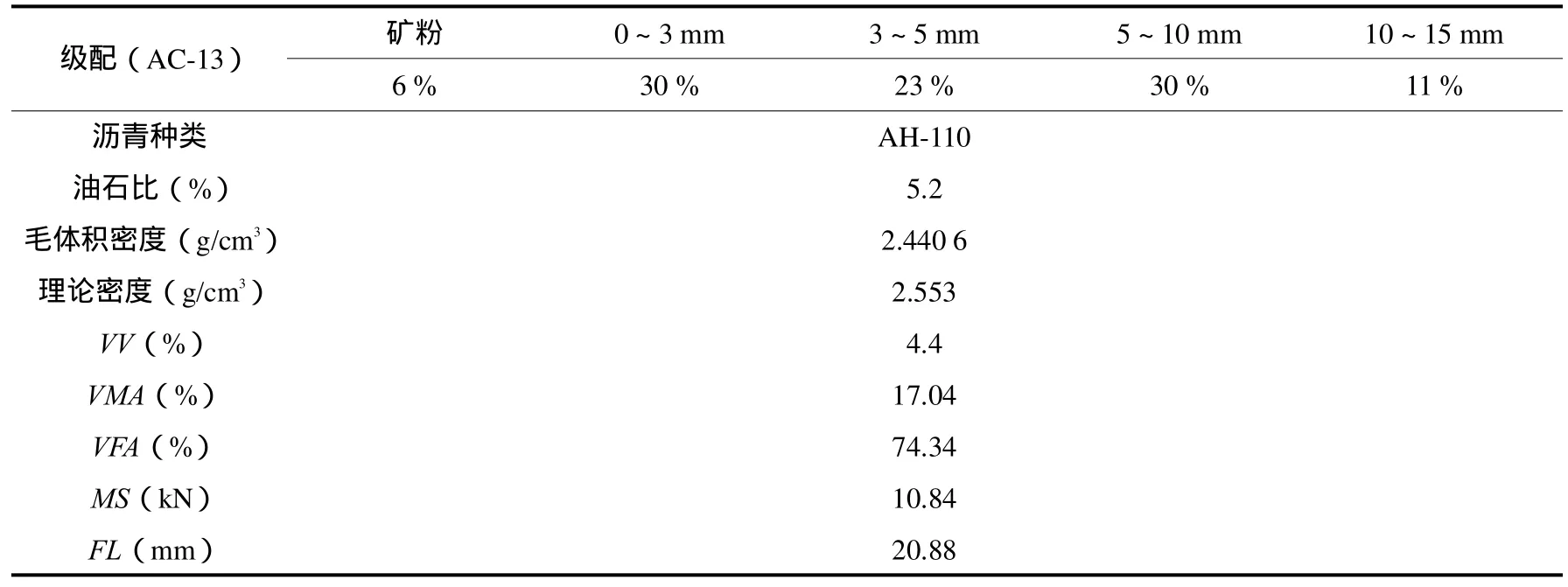
表3 沥青混合料的物理性能指标Tab.3 Property indexes of asphalt mixture

2.2 试验概述及数据采集

该试验采用逐级加载劈裂试验．操作步骤完全遵循劈裂加载试验规程[2]，但加载方式参照沥青混合料单轴压缩试验规程[3]．试验温度拟定为3种情况： 10℃、0℃、15℃，加载速率为5 mm/min．

由于试验采用自动数据采集系统，所以只需对系统采集的数据稍加整理即可得到所需要的数据，也即得到3种温度条件下试件的各级荷载及其相应的回弹变形．限于篇幅的约束，这里只列举几个代表性试件的数据，具体如表4所示．

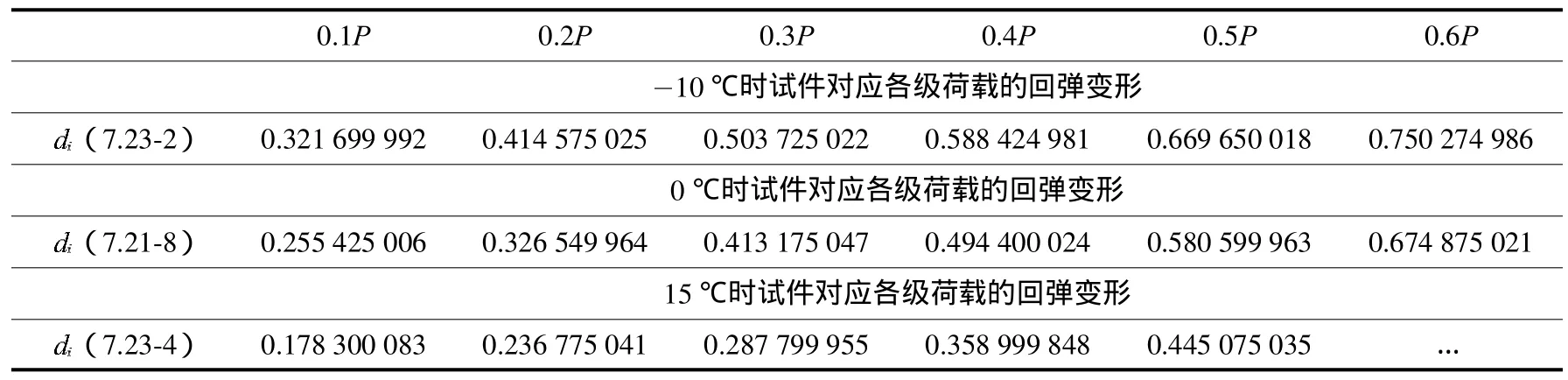
表4 3种温度条件下试件对应各级荷载的回弹变形 mmTab.4 Resilient deformation of specimens with every level of loading at three temperaturs

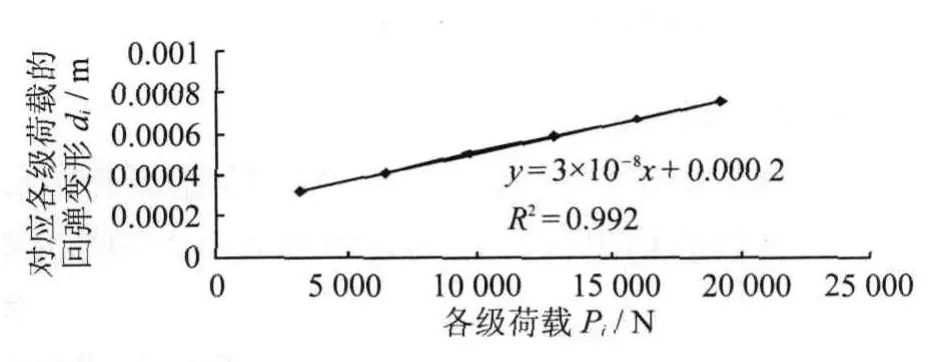
图3 与 的关系曲线Fig.3 Relationship curvebetweenand

表5 各级荷载所对应的回弹模量Tab.5 Resilient moduliwith every level of loading

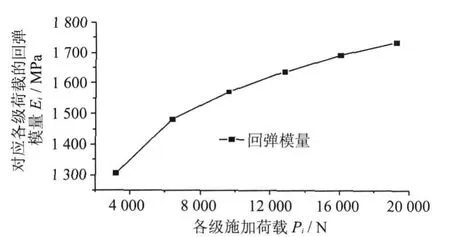
图4 各级荷载与对应回弹模量的关系曲线Fig.4 Relationship curvebetween loading level and resilient modulus

3 数据处理及分析

3.1 数据处理

3.1.1 回弹变形的线性修正

由于试验采集数据存在一定误差，需对其进行修正，具体回弹变形数据修正过程及步骤如下（以试件7.23-2为例）：

1）绘制各级荷载与相对应回弹变形的关系曲线图

根据劈裂试件7.23-2在各级荷载作用下的回弹变形测试数据绘出与的关系曲线并进行线性修正，如图3所示．

2）对各级荷载作用下的回弹变形进行线性修正

根据图3中的线性修正公式得到试件7.23-2的回弹变形修正值为0.000 2，也即将各级荷载下测得的回弹变形数据减去0.000 2即得修正后的回弹变形．

3）按上述两步骤计算其他试件回弹变形的线性修正值．3.1.2劈裂弹性模量的计算

仍以劈裂试件7.23-2为例，按照公式 (3)计算各级荷载所对应的回弹模量，具体计算结果如表5所示．

将该试件各级荷载作用下算得的回弹模量绘制成曲线图，具体见图4所示．

由图4可看出：各级荷载所对应的回弹模量并不相同，且随荷载等级的增加回弹模量值趋于稳定，说明回弹模量与施加荷载存在一定的依赖关系，但理论上来说回弹模量与施加荷载是不存在依存关系的，也即回弹模量是反映材料本身固有特性的一个力学指标，不随施加荷载变化而变化，所以在确定各试件的回弹模量时需选择模量值稳定的荷载等级．由图4和表6中数据可知：第五级荷载所对应的回弹模量趋于稳定．且为了与沥青混合料抗压回弹模量试验规程中荷载等级的取法相对应．选择第五级（0.5）荷载作为试件回弹模量计算的荷载等级是合理可行的．因此试件7.23-2的劈裂弹性模量为1 692.536 1．

同样其他试件劈裂回弹模量的计算完全遵循上述数据处理步骤．

3.2 数据处理结果及分析

按照上述的数据处理过程算出各种温度下对应一组试件的劈裂回弹模量，然后取其平均值并规定一定的保证率即得该温度条件下的劈裂回弹模量．具体汇总结果如表6所示．

从表6中的数据可以看出：沥青混合料的劈裂回弹模量随温度的降低而增大，低温下（ 10℃、0℃）的劈裂回弹模量与常温下的劈裂回弹模量相差很大，几乎呈2～3倍关系．说明温度对沥青混合料的劈裂回弹模量影响较大．

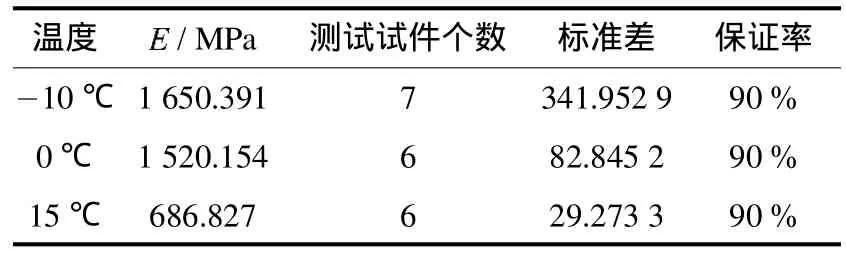
表6 3种温度条件下沥青混合料的劈裂回弹模量Tab.6 Resilient moduliof asphalt mixture under splitting loading at three temperatures

4 3种受力方式下弹性模量的比较分析

4.1 弹性模量的比较分析

由于没有进行其他两种受力方式下的试验测试，所以这里只能参照相关资料对3种弹性模量进行定性比较分析．参考康伟利用小梁弯曲试验测得的各种温度条件下沥青混合料弯拉弹性模量[4]以及姚爱玲等拟合出的沥青混合料抗压回弹模量与温度的关系式[5]（侧面法），大致可以看出：同一温度条件下，不同受力方式的试验方法测得的沥青混合料弹性模量相差很大，抗压回弹模量比弯拉弹性模量和劈裂回弹模量都大；10℃时抗压回弹模量大约是劈裂回弹模量的4倍；0℃时大约为2.5倍，但该温度条件下的弯拉模量与劈裂回弹模量却几乎接近；15℃时抗压回弹模量大约是劈裂回弹模量的1.5倍．

4.2 对路面结构受力的影响分析

具体以轮隙中心处的层底拉应力作为衡量指标，以分析弹性模量对沥青路面结构层受力的影响．假定沥青路面结构层及各层材料参数为：上面层为4 cm厚的细粒式沥青混凝土，泊松比为0.25；下面层为6cm厚的粗粒式沥青混凝土，泊松比为0.25；基层为20cm厚的水泥稳定砂砾，泊松比为0.25；垫层为20cm厚的级配碎石，路面结构下是压实的土基，泊松比为0.35．在分析计算相应于轮隙中心处的基层底部拉应力时，各结构层的模量开始均取为15℃的抗压回弹模量值，也即从上向下各层材料的模量大致取为1 400 MPa、1 400 MPa、2 000 MPa、350 MPa、45 MPa，然后同时降低上面3层材料模量的10%、20%、30%、40%、50%，利用Bisar程序计算分析相应的基层底部拉应力变化情况．计算结果表明：相应于模量的变化幅度，基层底部拉应力则分别降低7.03%、14.85%、23.50%、33.09%、43.94%．材料模量变化范围正好大致是抗压回弹模量变化到劈裂回弹模量的范围，而从基层底部拉应力的变化情况表明：路面结构中材料弹性模量的变化对于结构层的受力具有较大的影响，材料模量降低，基层底部拉应力也会随之降低，但降低的幅度比模量的降低幅度小．因此沥青路面设计规范采用抗压回弹模量来检验层底拉应力时，则是偏于安全角度考虑的，而劈裂回弹模量的采用能与检验指标容许拉应力（劈裂强度除以抗拉结构系数）相互对应，是较为适宜的．

5 结论

1）运用有限元程序对沥青混合料的劈裂试验进行数值模拟，拟合出施加应力、弹性模量、施荷点处的变形三参数之间的关系式，从而推导出弹性模量的计算公式．

2）对具体一个马歇尔试件的劈裂弹性模量的计算过程进行了详细描述，也即对试验数据的详细处理过程．最后算汇总了3种温度条件下沥青混合料的劈裂弹性模量并进行了数据分析．

3）与小梁弯拉试验所测得的弹性模量以及抗压回弹模量进行了比较分析，并就3种弹性模量对路面结构受力的影响进行了分析．

[1]JTGD 50-2006，公路沥青路面设计规范 [S]．

[2]T 0716-1993，沥青混合料劈裂试验规程 [S]．

[3]T 0713-2000，沥青混合料单轴压缩试验规程（圆柱体法）[S]．

[4]康伟．沥青路面面层抗裂性能试验研究 [D]．西安：长安大学，2006.20-29．

[5]姚爱玲，张西玲，王选仓．测试方法对沥青混合料抗压回弹模量的影响 [J]．长安大学学报，2005，25（6）：21-24．