降落伞拉直过程的三维仿真分析

史献林 余 莉 袁文明 刘卫华

(南京航空航天大学 航空宇航学院,南京210016)

引言

降落伞拉直过程是降落伞开伞过程的一个重要阶段,早期拉直过程动力学模型,都是假设伞系统和气流方向一致,处于理想的直线状态。但降落伞在拉直过程中,由于高空风或回收物的摆动等多种因素的影响,降落伞的拉直方向几乎不可能与气流速度方向一致,从而导致伞绳拉出部分出现“弯曲”现象,即“绳帆”现象。从上世纪70年代开始,国外陆续开展了一系列旨在消除“绳帆”现象的实验和理论分析的研究工作:Moog建立了简单的弹性质点模型对“绳帆”进行了一定程度的模拟[1];Wolf基于变质量动量方程,建立了连续拉出模型计算拉出时伞绳张力[2];Purvis在1983年首次提出了多质点阻尼弹簧模型,成功再现了“绳帆”现象[3]。上世纪90年代后,国外对拉直过程的研究逐渐减少。国内对“绳帆”现象的研究开始较晚,2003年,张青斌等提出了多刚体模型,对拉直过程中的有关现象进行了较全面的分析[4]。

国内外研究人员成功地模拟了二维平面上的拉直过程,通过增加引导伞面积,有效抑制了“绳帆”现象[3]。然而,随着我国载人飞船降落伞回收系统的不断发展,一些需要进一步深入研究的现象,如伞绳(伞衣)与主伞包摩擦,主伞伞衣局部破损等,已有的二维模型已经不能胜任,迫切要求建立三维的动力学仿真模型,分析这些现象的空间动力学特性。

本文经过充分调研收集数据,在二维模型的基础上,建立了三维多体系统动力学模型,仿真分析了不同高空风场条件下的拉直过程,指出侧风时,拉直时间最短、拉直力最大,对拉直过程的性能影响最显著。拉直过程仿真研究有助于更加深入地理解降落伞拉直过程的工作机理。

1 数学模型

图1(a)是某载人飞船降落伞回收系统主伞拉直过程中的组成部分,包括减速伞、主伞包、主伞伞衣、主伞伞绳、主伞连接带、返回舱吊带、返回舱等。图1(b)为倒拉法[5]主伞拉直过程,分为两个阶段:1)减速伞从返回舱中拉出主伞包;2)在减速伞和返回舱速度差作用下,依次从主伞包中拉出主伞连接带、主伞伞绳和主伞伞衣,直至全长拉直。本文经过二维建模实践和充分调研,以多体系统动力学理论[6]为指导,建立由一系列刚体和质点通过弹性约束组成的拉直过程三维动力学模型,参考图1(c)。模型中,将减速伞视为由质点系构成的刚体,根据质点系动量定理和质点系相对于任意动点的动量矩定理[7],可推导出六自由度的降落伞质点系动力学方程[8],此模型体坐标系原点选取在压力中心,能够分析降落伞各部件质量的影响;主伞包为变质量体,质量不断减小,建立六自由度变质量动力学方程[7];将柔性大变形的吊带、主伞伞绳、主伞伞衣、牵顶伞连接带等离散成以若干首尾相连的绳段,各绳段假设为质量集中在端点的三自由度质点,各质点之间以阻尼弹簧相连,已拉出质点的运动由对应绳段的重力、气动力和张力决定[1-4],正在拉出质点采用Wolf的连续拉出假设[2]计算拉直力,未拉出质点随主伞包一起运动;返回舱采用六自由度的刚体动力学模型[5];阻尼弹簧只传递张力,不传递力矩。

图1 某载人飞船降落伞回收系统主伞拉直过程

2 动力学模型正确性和仿真结果有效性验证

为了验证拉直过程三维多体系统动力学模型的正确性和仿真结果的有效性,根据某载人飞船的空投试验数据和录像,确定了拉直过程的主要初始参数,然后基于Matlab平台,自编程序,采用变步长龙格库塔法求解三维动力学微分方程。图2是仿真分析模型的流程图,给出了动力学方程以及各主要参数之间的相互关系。其中,u、ν、w分别代表研究对象的当地空速、地速及风速;α、β表示它们的气动迎角和侧滑角;Q、G、T则表示对应的气动力、重力和张力;m、s、E表示该研究对象的质量、位移及弹性模量;Δs、sy表示位移差及y向位移。表1是仿真结果与某飞船空投试验数据的比较。

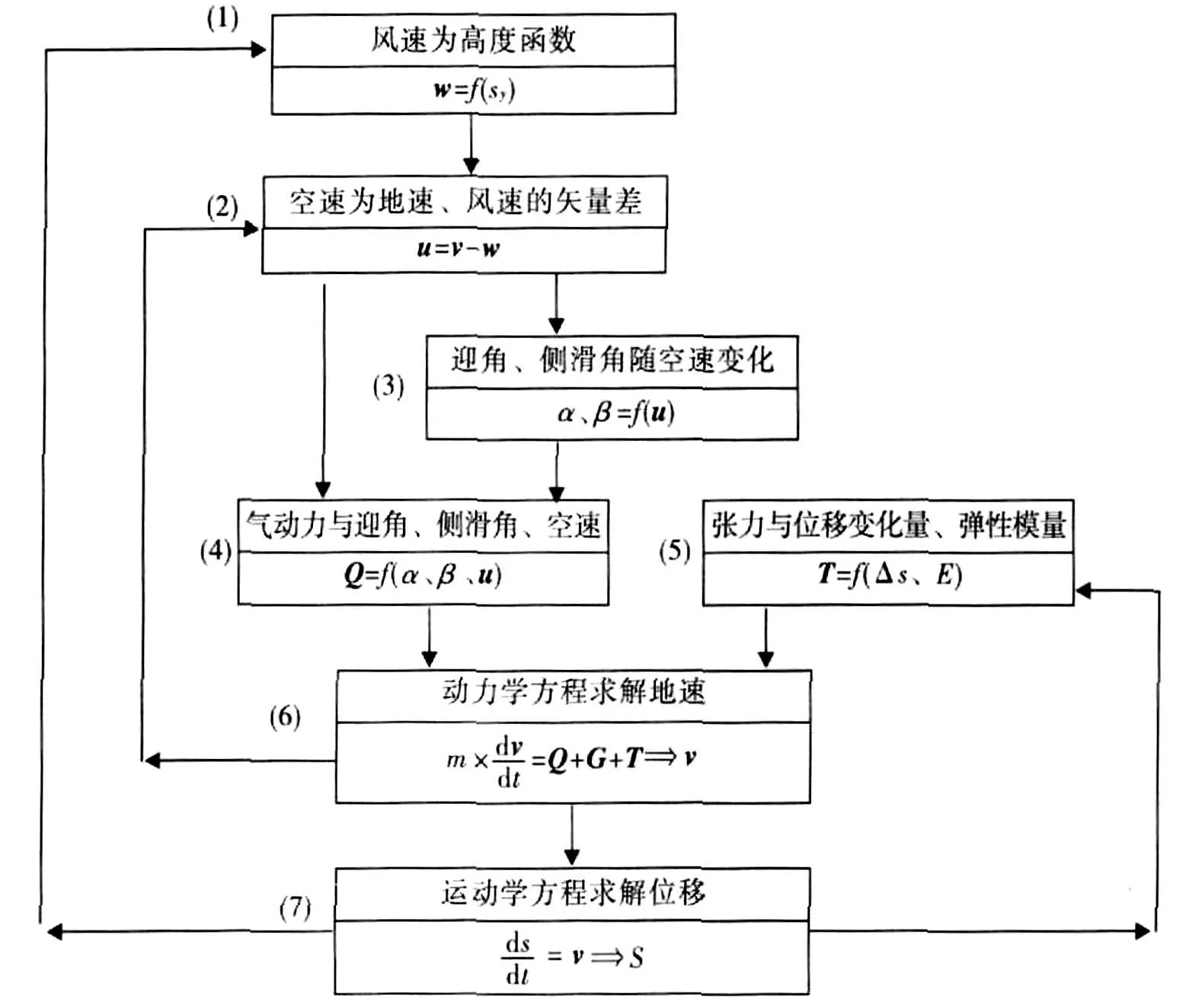
图2 模型中主要参数的关系

表1 仿真结果比较

图3为拉直过程中返回舱、主伞包和减速伞速度随时间的变化曲线。返回舱速度从初始速度95m/s缓慢增加到102m/s,拉出伞衣后,速度基本保持不变。主伞包和减速伞速度变化规律相同,速度从95m/s平稳减速到26m/s;质点在未拉出主伞包时,跟随主伞包一同运动,质点拉出时间非常短暂,从主伞包速度迅速加速到返回舱速度,在拉出伞衣底边时,速度开始剧烈振荡。

图4为质点拉出速度随时间的变化曲线。本模型中拉出速度等于主伞包速度与正在拉出质点速度的差。伞绳质点拉出时,拉出速度近似等于返回舱和主伞包的速度差,从0m/s增加到70m/s;拉出伞衣底边质点时,拉出速度从70m/s迅速降低到约43m/s,这是因为此时张力从2 030N瞬间增加到38 000N,产生一个较大的负向加速度,正在拉出质点速度较小;伞衣质点拉出时,由于质点速度围绕返回舱速度振荡,拉出速度跟随波动,整体趋势在增速;在伞衣顶部质点拉出时,达到最大87m/s。

图3 返回舱、主伞包、减速伞及各质点速度变化

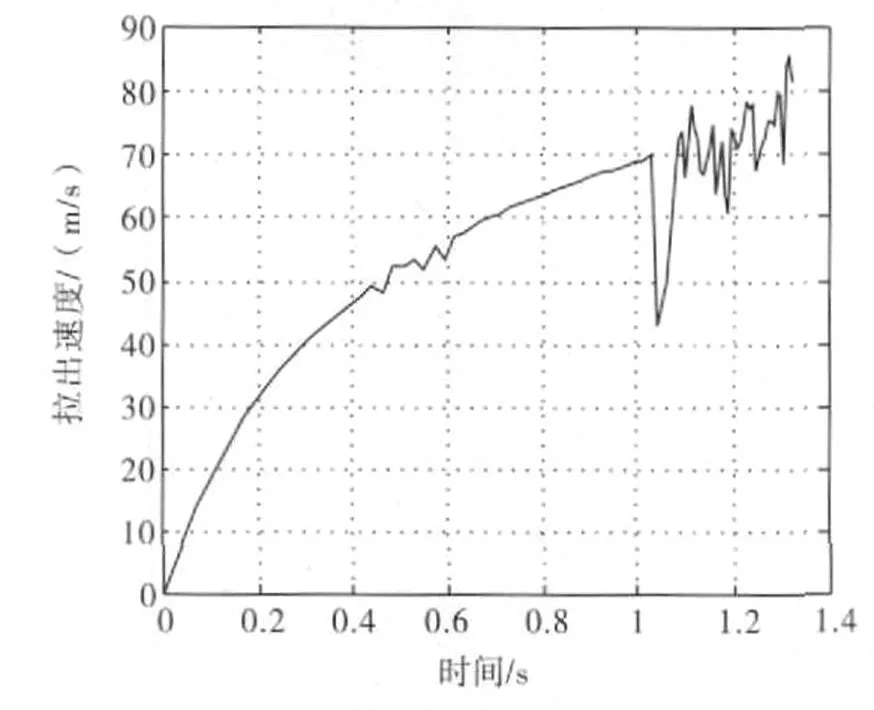
图4 拉出速度随时间的变化曲线

图5 伞绳张力随时间的变化曲线

图5 是伞绳张力随时间的变化。最大伞绳张力约39 200N,出现在拉出伞衣底边附近。伞绳张力的变化趋势与理论分析及相关文献[4-5]描述一致。伞绳拉直时,张力缓慢增加到2 020N,拉出伞衣底边后,张力瞬间增加到38 000N,然后短暂振动后,下降到25 000N左右。由图2中动力学方程公式(流程6),质点张力的变化将导致该质点速度改变。图6为不同时刻主伞各质点拉直过程位置示意图。伞绳(伞衣)没有出现明显的弯曲现象。返回舱轨迹相对初始轨迹几乎保持不变,但减速伞随风飘动明显。上述结果与试验录像和文献[4]计算结果相近。

通过表1、图2～图6关于拉直时间、拉直力、速度、质点拉出速度、伞绳张力、位移的变化,验证了本文建立的三维动力学模型的正确性及仿真结果的有效性。

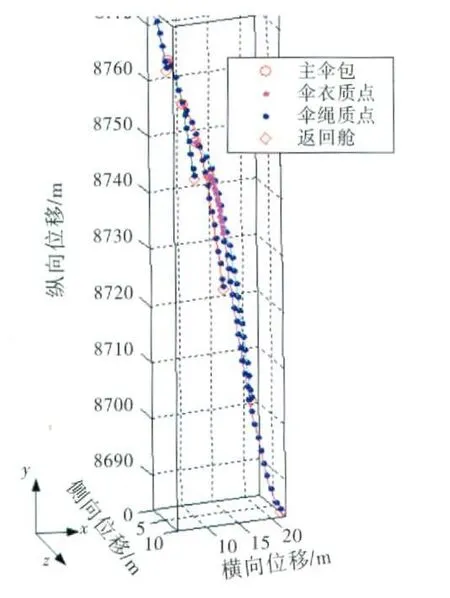
图6 拉出过程质点位置示意图

3 不同高空风场条件下仿真结果的对比

3.1 风向的表示方式

气象学上,风向指风吹来的方向[9],而风速w方向为风吹向的方向,故与风向相反。本文地面坐标系为东南坐标系[5],风向与地面坐标轴之间的关系为东风(东向90°)对应oxd轴,南风(南向180°)对应ozd轴,见图7。在文献和空投试验中,通常将测量的风向和风速表示成高度的函数,并且忽略垂直方向的风效应,即wy=0,风场简化为水平风场,见图7。设风向σ=g(y),风速w=f(y)。则在地面坐标系下,三维风场的函数见式(1):

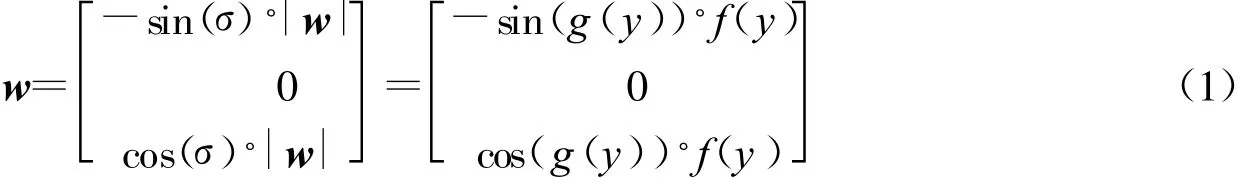
为了更方便的衡量风速w偏离初始拉直速度的角度,将风速w方向与地速υ在风速水平面投影的夹角定义为风速偏角δ(见图7),则δ=0°时为顺风,δ=180°时为逆风,δ=90°时为侧风。δ与σ的关系,见式(2)

式中 τ为地速 v在风速水平面投影与北风(北向0°)的夹角,见图7。

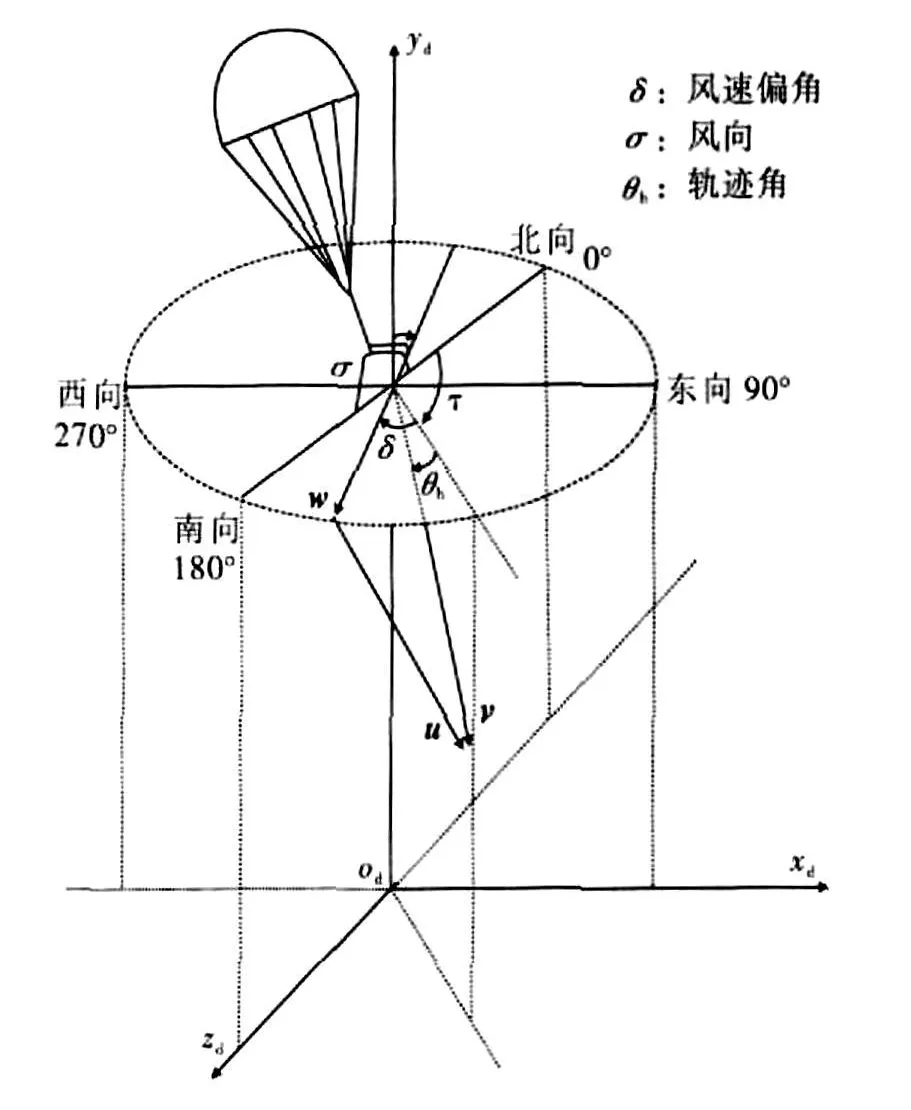
图7 风速偏角的定义

3.2 仿真结果与分析

模拟了初始的风速从0～60m/s,间隔5m/s,计12组;风速偏角δ从 0°～180°(从顺风到逆风),间隔 50°,计13组;合计12×13共156组高空风场状态下的三维拉直过程。统计分析了拉直时间、拉直速度的整体变化规律。

风场的仿真计算结果表明:风速偏角变化将使得迎角和侧滑角发生改变。顺风、逆风气动角改变相反,而侧风状态将会产生较大的侧滑角,从而引起气动力三维分量发生明显改变。而风速越大,对这种变化影响更为显著。图8、图9分别为拉直时间随风速偏角和风速的变化情况;图10、图11则为拉出速度的变化情况,结合上述图形,可以得到以下规律:

1)不同风速下的拉直时间,侧风时最短存在明显驻点,逆风时次之,顺风时最长。

2)顺风时,拉直时间从1.27s随风速增加延长到1.5s,风速影响较大。

3)逆风时,拉直时间从1.27s随风速增加平稳下降到1.2s,风速影响较小。

4)侧风时,拉直时间从1.27s随风速增加减小到0.95s,风速影响最大。

5)不同风速下的平均拉出速度,侧风时最大存在明显驻点,逆风时次之,顺风时最小。

6)顺风时,平均拉出速度从75m/s随风速增加逐渐减小到约66m/s,风速影响较大。

7)逆风时,平均拉出速度随风速增加在75～78m/s之间小幅度振动,风速影响很小。

8)侧风时,平均拉出速度从75m/s随风速增加逐渐增加到约90m/s,风速影响较大。

参考图2中各参数之间的关系,上述规律主要是由于气动力[5,10]不同造成的。侧风时迎角为零,切向(轴向)阻力最大[5,10],产生较大的负向加速度,造成减速伞和已拉出伞绳(伞衣)减速,而对返回舱速度影响很小(见图3),拉出速度增加,拉直时间变短;顺风时v、w同向,减速伞和已拉出伞绳(伞衣)随风漂移,拉出速度减小,拉直时间增加;逆风时v、w反向,减速伞和已拉出伞绳(伞衣)被风吹袭,拉出速度增加,拉直时间减小。

图8 拉直时间随风速偏角的变化

图9 拉直时间随风速的变化

图10 平均拉出速度随风速偏角的变化

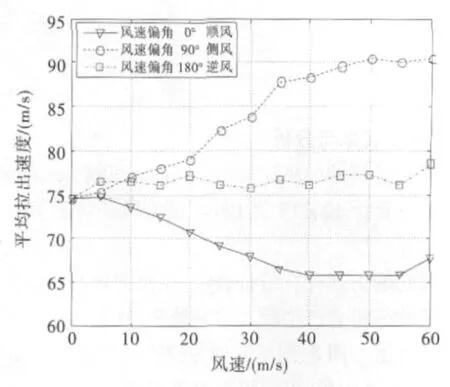
图11 平均拉出速度随风速的变化

4 结束语

本文在充分调研和二维建模的基础上,首次建立了降落伞回收系统拉直过程的三维动力学模型。首先,在空投试验条件下通过了正确性和仿真结果有效性的验证;接着,提出了风速偏角的概念以定义风速 w与地速v的角度关系;最后,在合计12×13共156种高空风场中,模拟了空间拉直过程,总结分析了拉直时间与拉出速度的变化规律,指出侧风对拉直过程性能的影响最大,分析了出现此规律的动力学机理。本文的研究工作能够为拉直过程的建模仿真提供一定的参考和指导作用。

[1]Moog PD.Aerodynamic line bowing parachute deployment[R].AIAA 75-1381,1975.

[2]McVeigh D F,Wolf D F.Analysis of deployment and inflation of large ribbon parachute[J].J.Aircraft,1974,11(2):96-103.

[3]Purvis JW.Improved Prediction of Parachute Line Sail during Lines-First Deployment[R].AIAA 84-0786,1984.

[4]张青斌,彭勇,程文科,等.降落伞拉直过程的多刚体模型[J].中国空间科学技术,2003,23(2):45-50.

[5]王利荣.降落伞理论与应用[M].北京:宇航出版社,1997:137-187.

[6]休斯敦R L,刘又午.多体系统动力学[M].天津:天津大学出版社,1991.

[7]洪嘉振,杨长俊.理论力学[M],北京:高等教育出版社,2002.

[8]史献林,余莉,袁文明.一种新的降落伞动力学模型[C]∥中国航空学会全国第十二届安全救生学术交流会文集.贵阳:中国航空学会安全救生专业委员会,2008.

[9]中国科学博览.风向[EB/OL].http://www.kepu.net.cn/gb/earth/weather/wind/.

[10]Ibrahim S K,Engdahl R A.Parachute Dynam ics and Stability analysis[R].NASA-828607.1972.