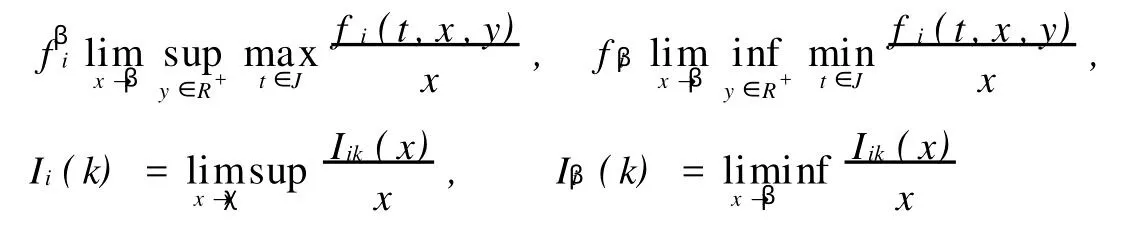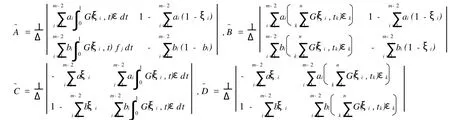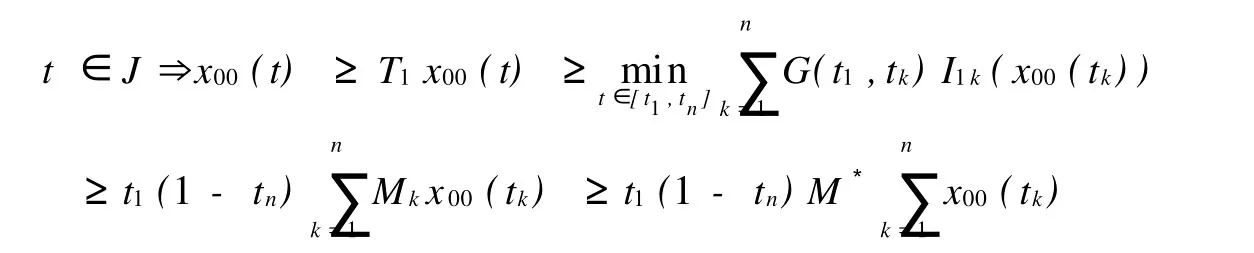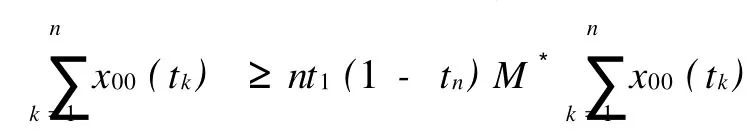二阶非线性m 点脉冲微分方程组的正解*
2010-10-09薛妮娜孙艳梅
薛妮娜,孙艳梅
(潍坊学院,山东 潍坊 261061)
二阶非线性m 点脉冲微分方程组的正解*
薛妮娜,孙艳梅
(潍坊学院,山东 潍坊 261061)
利用锥上的不动点定理讨论了二阶非线性m点脉冲微分方程组(1)的解,得到了解的存在性定理。
不动点定理;正解;全连续
0 引言
考虑下列二阶m点带有脉冲项的方程组

其中J=[0,1],fi∈C(J×R+×R+,R+),Iik∈C(R+,R+),i=1,2;R+=[0,+∞],0 对二阶非线性微分方程边值问题的研究已有许多结果,本文在较弱的条件下利用锥上的不动点定理研究了方程组(1)正解的存在性,其结果包含、推广了许多相关的结果。 PC′[0,1]={X∈C[0,1];x′|(tk)tk+1∈C(tk),tk+1},x′(t-k)=x′(tk),k=1,2,…,m},在范数‖x‖pc′=max{‖x‖,‖x′‖}下,PC′[0,1]成为Banach空间。其中‖x‖=stu∈pJ|x|,J′=J{t1,t2,…,tn}。在范数‖(x,y)‖pc′=max{‖x‖pc′,‖y‖pc′}下。PC′[0,1]×PC′[0,1]成为Banach空间。 定义1.1(x,y)∈PC′(J,R+)∩C2(J′,R+)×PC′(J,R+)∩C2(J′,R+)是(1)的解,当且仅当(x, y)满足(1)。 引理1.1 假设Δ≠0,则(x,y)∈PC′(J,R+)∩C2(J′,R+)×PC′(J,R+)∩C2(J′,R+)是(1)的解,当且仅当(x,y)是积分方程组(2)的解。 其中 引理1.2 若 注1 从式(3)可知 令K={x∈PC′[0,1],x≥0,x(t)≥t1(1-tn)x(s),t∈[t,tn],s∈J} 定义算子T1和T2 令T(x,y)(t)=(T1(xy)(t),T2(xy)(t)) 引理1.3 假设条件(H1)成立,则T(K×K) 证明 对任意(x,y)∈K×K,有T1x≥0, 另一方面,由于t1(1-tn)≤1 从而,(T1(x,y))(t)∈K。 类似可证(T2(x,y))(t)∈K,即T(K×K) 令 这里β代表0+或+∞,i=1,2。 定理2.1 假设条件(H1)成立,再假设fi和Iik满足下列条件 则方程组(1)至少有一个正解。 证明 由条件(H2)知,对Πε,εk>0存在0<γ<η,使得fi(t,x,y)≤εγ,Iik(x)≤εkγ,i=1,2, k=1,2,…n,对0≤x≤γ,t∈J。其中ε,εk满足这里 下面证明T(x,y)≥(x,y),(x,y)∈K×K,‖(x,y)‖=γ。若存在(x1,y1)∈K×K,‖(x,y)‖=γ,使得T(x1,y1)≥(x1,y1),那么 故 ‖x1(t)‖PC′<‖x1‖PC′。 类似可证‖y1(t)‖PC′<‖y1‖PC′,从而‖(x1,y1)‖<‖(x1,y1)‖矛盾。 考虑条件(H3)第一种情形,fi∞=∞,(i=1,2),则存在τ>0,使得 f1(t,x,y)≥Mx,t∈J≥τ,其中M>[t1(1-tn)(tn-t1)]-1,选取R>max{γ,τ[t1(1-tn)]-1}。 下面证明T(x,y)Κ(x,y),(x,y)∈K,‖(x,y)‖=R,若T(x0,y0)≤(x0,y0),‖(x0,y0)‖=R。 分为两种情形:(Ⅰ)‖x0‖pc=R,‖y0‖pc≤R;(Ⅱ)‖y0‖pc=R,‖x0‖pc≤R。 (Ⅰ)若‖x0‖pc=R,则x0(t)≥t1(1-tn)x0(s),t∈[t1,tn],s∈J,从而 从而M≤[t1(1-tn)(tn-t1)]-1矛盾。 同法可证若‖y0‖pc=R的情形,即T(x,y)Κ(x,y),(x,y)∈K,‖(x,y)‖=R。(Ⅱ)Ii∞(k)=∞,k=1,2,…,n,i=1,2,则存在τ1>0,使得I1k≥Mkx,x≥τ1,其中Mk>[t1(1-tn)]-1,k=1,2,…,n 令M3=min{Mk:k=1,2,…,n},则M3>[t1(1-tn)]-1。 选取R>max{γ,t1[t1(1-tn)]-1,下证T(x,y)Κ(x,y),(x,y)∈K,‖(x,y)‖=R。 类似于第一种情形(分两种情形) 事实上,若存在x00×y00∈K×K,‖(x00,y00‖=R,使得T(x00,y00)≤(x00,y00),若‖x00‖pc=R则 因此 从而 因此 由M3定义,可得 类似于第一种情形,可证,从而得到矛盾。 即T(x,y)Κ(x,y),(x,y)∈K,‖(x,y)‖=R。 利用锥拉伸与压缩不动点定理,可知T至少有一个不动点(x,y)=Kr,R×Kr,R={(x,y):r≤‖(x,y)‖≤R},即方程组(1)至少有一对正解。 定理2.2 将定理2.1的条件(H2)、(H3)换成(H4)fi∞=0且Ii∞(k)=0,k=1,2,…,n,i=1,2(H5)fi0=∞或Ii0(k)=0,k=1,2,…,n,i=1,2 定理2.1的结论也成立。 [1]Feng M Q,Xie D X.Ultiple positive solutions of multi-point boundary value problem for second-order impulsive differential equations[J]. Journal of Computational and Applied Mathematics,2009,223:438-448. [2]刘炳妹,刘立山.二阶方程组解得存在唯一性[J].工程数学学报,2007,24(4):757-760. (责任编辑:刘乃生) O175.14 A 1671-4288(2010)04-0075-04 2009-10-20 薛妮娜(1978-),女,山东安丘人,潍坊学院数学与信息科学学院讲师。研究方向:非线性泛函分析及应用。1 预备知识及引理


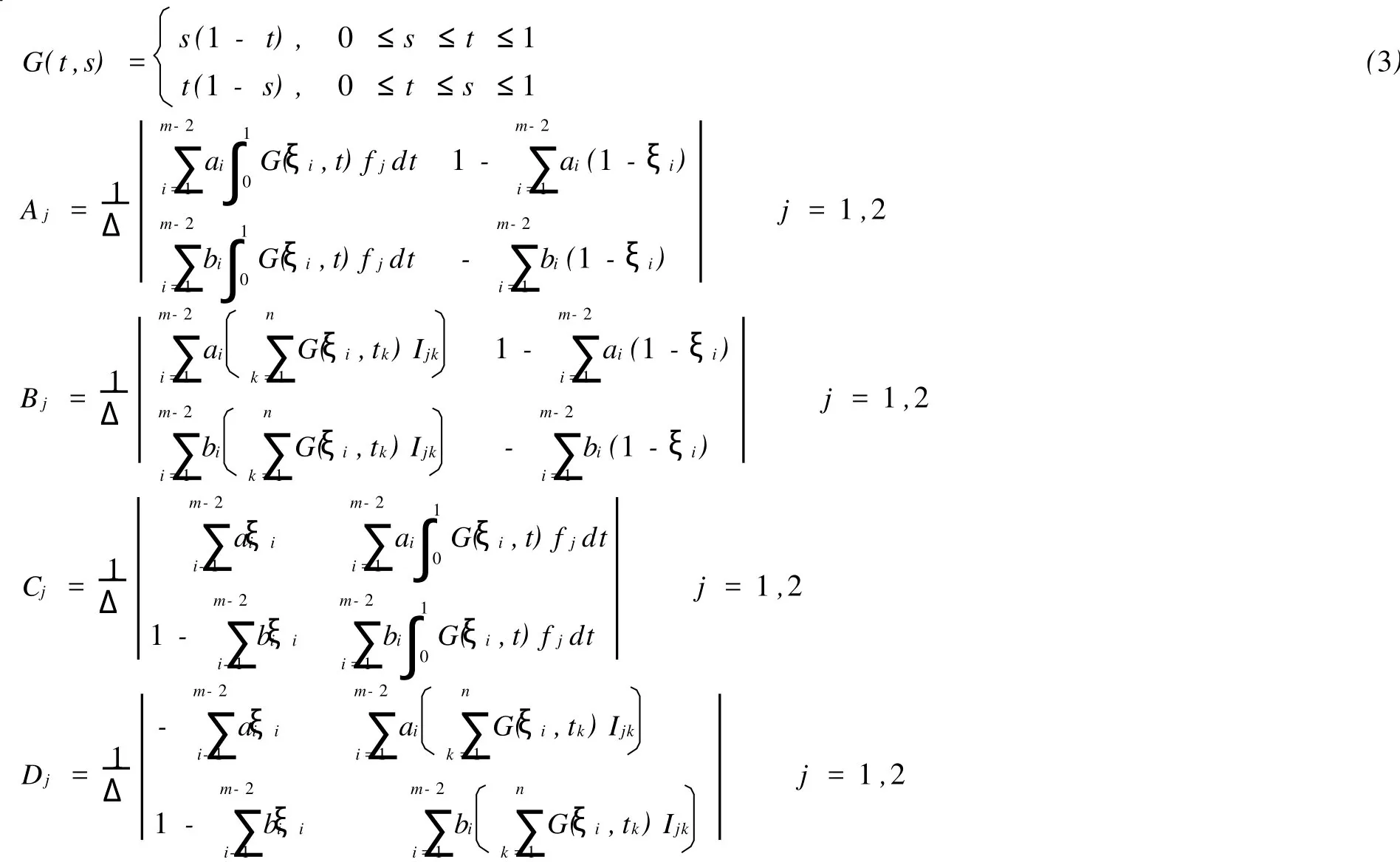

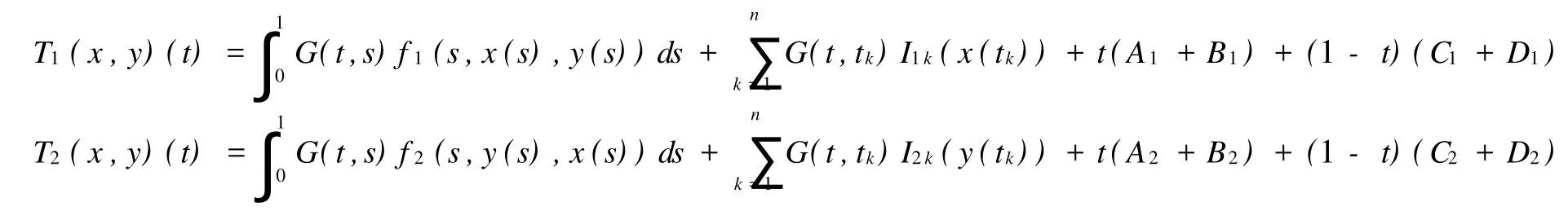


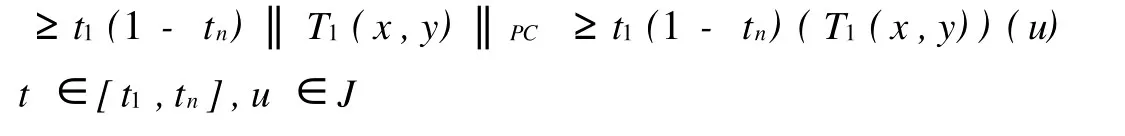
2 主要结果