基于小波变换的ECG去噪法及仿真

席朝岭，邱联奎

河南科技大学 电信学院，河南 洛阳471003

基于小波变换的ECG去噪法及仿真

席朝岭，邱联奎

河南科技大学 电信学院，河南 洛阳471003

为去除心电信号中的各种噪声，本文以小波变换的多分辨率分析为理论基础，利用自适应阈值调整小波变换系数，用调整后的系数进行心电信号重建。采用MIT-BIH数据库中的心电信号进行仿真、验证，有效地去除了噪声信号。与传统滤波器具去噪相比有明显的优越性。

ECG；小波变换；心电信号仿真；去噪

0 前言

心电信号(ECG)记录了心脏的电生理现象，客观地反映了心脏各个部位的生理状况，为临床诊断提供了心脏功能及疾病的重要信息。由于心电信号比较微弱，幅值范围在50µV ～5mV之间，频率主要在0.05 ～100Hz范围之间，90%的心电信号频谱在0.25～35Hz之间[1]，在信号采集时，易受仪器、病人及环境等因素的影响，会产生基线漂移。受人体肌电、50Hz工频和其它噪声的干扰，心电信号往往会被淹没在较强的背景噪声之中[2]。传统的数字滤波方法大都针对某种噪声单独设计滤波器，对心电信号中的其它干扰不起作用。由于心电信号微弱、信噪比低、奇异点较多以及有用信号频带与噪声频带相互重叠等，使得传统的滤波去噪方法在处理心电这种短时低能量的瞬变信号时，信噪比的提高往往是以信号局部特征的损失为代价的。如何处理保留心电信号局部特征和有效抑制噪声之间存在的矛盾，是心电信号去噪的关键。近年来，随着小波理论研究和应用的不断深入，小波变换由于具有良好的时频局部化特性，它被逐渐运用到心电信号处理之中，成为缓解、处理上述问题的一种新手段。

1 小波变换去噪原理

小波的多分辨率分析特性能将信号在不同尺度下进行多分辨率分解，由于有用信号和噪声信号的频率存在差异，所以在不同分解尺度上的小波系数呈现不同特征。这样小波去噪就是利用多分辨率时频局部化特性，把信号中的不同频率成分分解到不同的尺度空间上，然后对各个尺度下的小波系数利用阈值进行处理，去掉由噪声引起的小波系数，保留由有用信号引起的小波系数，用处理过的小波系数进行反变换，得到去噪后的信号[3]。

1.1 小波基的特性

小波基的数学特性主要有：① 正交性。正交性是小波基的一个非常优良的性质，能够保证信号的精确重构。②正则性。正则性又称规则性,它用于描述信号在某点或某一区间内的光滑性和奇异性，主要影响着小波系数重构的稳定性。③ 消失矩。由数学分析的知识可知，一般光滑函数都能用多项式来描述(如Taylor展开)，因此小波的消失矩越高，光滑函数在小波展开式中的零元就越多(实际小波变换中，严格为零的小波系数也很少) ，消失距越高计算得到的零元越多，对数据压缩非常有用。④ 紧支性。紧支性是小波的重要性质，支集越短的小波，局部化能力越强，越有利于确定信号的突变点，而且支集越短的小波，产生的大幅值的小波系数就越少，这与实际中希望小波系数的幅值尽可能小相一致。此外，短支集能提高计算速度，这对心电信号的实时处理也是十分重要的。⑤ 对称性。对称性是描述小波性能的一个基本特征。小波具有对称性意味着进行Mallat分解时的滤波器组具有线形相位,可以避免信号分解和重构时的相位失真，是刻画小波性能的一个基本特征[4]。

1.2 心电信号去噪中小波基的选择

小波变换的小波基不具备唯一性, 不同的小波基具有不同的时频特性，选取不同的小波基对同一心电信号进行处理，将得到不同的结果，所以，在小波变换去噪中，小波基的选取是影响小波去噪效果的一个主要因素。小波基的选择也是小波变换去噪中的一个难点，一般情况下，小波基的选择难以统一成一般原则。实际应用中，根据上文所述小波的数学特性，根据要处理信号的特点，针对具体问题进行具体分析，通过经验或不断的试验来选择小波基，用小波变换方法处理信号的结果与理论结果来判定小波基的好坏，由此确定最优的小波基。下面简单介绍几种常见的小波基：

(1) Haar小波。它的优点是它是唯一一个具有对称性的紧支正交实数小波，支撑长度为1，做小波变换时，计算量很小。它的缺点就是光滑性太差，用它重构的信号，会出现“锯齿”现象。Haar小波的这种不连续性使其在实际的信号处理中失去了使用价值，因此不适于处理心电信号。

(2) Marr小波和Morlet小波。它们的优点是具有清晰的函数表达式，且具有对称性，但是它们的尺度函数不存在，不具有正交性，这就不能够对分解后的信号进行重构，所以也不适于心电信号去噪。

(3) Meyer小波。它是紧支撑正交对称小波，无穷次连续可微，有无穷阶消失矩。但它没有快速算法，影响计算速度，对心电信号来说，实时处理、分析的数据量较大，所以从处理速度方面考虑，一般不采用Meyer小波。

(4) Biorthogonal小波。它是具有对称性的紧支双正交小波，可以用来实现心电信号去噪，但因为该小波系中的各小波基不具有正交性，只具有双正交性，相比具有同样消失矩阶数的正交小波来说，计算的简便性和计算时间可能会受到影响，所以应用时要合理选择滤波器的长度。

(5) Daubechies小波。它是一类紧支正交小波，通常表示为dbN的形式，其中N对应了小波函数的消失矩的阶数，且支撑长度为2N-1，正则性随着N的增加而增加，这些对于心电信号去噪来说都是很好的特性。但该类小波对称性很差，导致信号在分解与重构时相位失真严重，所以该类小波不太适合心电信号去噪。

(6) Smylet小波。它是近似对称的一类紧支正交小波函数，它具有Daubechies小波系的一切良好特性，在对称性方面进行的改进,使该小波系在处理心电信号时，可以很大程度避免不必要的失真，因此适合对心电信号去噪。

(7) coiflet小波。它也是一类具有近似对称性的紧支正交小波。消失距为N时，支撑长度为6N-1，理论上它可以用于心电信号去噪，而且coifliet小波symN小波的对称性要好一些，但这是以支撑长度的大幅度增加为代价的, coiflet具有与smy3N相同的支撑长度。对于心电信号来说，由于数据量较大，我们希望所选取小波的支撑范围尽量短，这样有利于节省处理时间，所以从计算时间上考虑，该类小波不如snytelt小波系。

综上所述，在这几类常用的小波中，只有Biohrtgoonal小波系和symlet小波系比较适合于心电信号去噪，且各具优缺点：Biohrtogonal小波系严格对称但不正交，symlet小波系正交但不严格对称。将信号作小波变换后，由于尺度系数反映的是信号的概貌信息，所以尺度函数的波形越接近于信号的形状，越有利于在不同的分解尺度下保留原始信号的形态。通过比较，smyelt小波系中的各个小波基所对应的尺度函数更接近于心电信号中完整的P-QRS-T波，所以本文选择了symlet小波对心电信号进行去噪处理[5]。

1.3 小波分解层数的确定

小波分解层数(或称分解尺度)的确定非常重要，分解层数不同，去噪效果也不同，有时甚至差别很大。利用小波变换去噪时，通常利用信号和噪声的频率范围确定分解层数。根据心电信号及所含噪声的特点，本文使用symlet小波进行8尺度分解。

1.4 阈值函数的选取与阈值λ的确定

小波去噪的基本思想是：噪声与信号在各尺度(即各频带)上的小波系数具有不同的特点，这些特点是在小波域中，信号的能量相对集中在某几个位置上，而噪声的分布一般比较广。根据瞬时性的特点，信号表现为一些大的系数，而一些小的系数则更多的是由噪声和信号能量的突变所产生的。将各尺度上由噪声产生的小波分量去掉，这样保留下来的小波系数基本上就是原始信号的小波系数，再利用小波逆变换重构出原始信号。

由此可知：小波去噪的关键是如何选择阈值除去由噪声产生的小波分解系数分量。阈值的选择同样非常关键，如果阈值过小，则方差偏大，数据欠平滑，去噪后仍留有噪声；但阈值过大，会使数据过于平滑，信号的奇异性可能丧失，重要的信号特征会被滤掉，引起偏差[6]。目前应用最广泛的是Donoho提出的硬阈值和软阈值降噪方法。根据心电信号中噪声的特点，阈值的选取不能单一，硬阈值由于阈值函数不连续性会引起较大的方差，且不稳定，对数据小的变化比较灵敏。软闭值法能提供较好的光滑性，具有较好的去噪效果，但有时会损失过多的有用信号信息，不易于保持信号的特征。所以本文采用软阈值σ方法处理，选用自适应阈值来克服这种缺点。阈值选取公式如下：λ=σ/ln(j+z)[7]，其中，N为心电信号采样点数，j为本级尺度，z为常数，本文实验中取z=1。

1.5 小波变换去噪的步骤

小波变换去噪法是一种原理简单的去噪方法，它可以简单的分为以下几个基本步骤：

(1)根据需要选择小波基，确定分解层数，然后将含噪声的信号在不同尺度下进行小波分解，分解到不同频带内，得到含噪信号的小波系数。

(2)根据上述自适应阈值法对小波系数进行阈值操作，得到新的小波系数。

(3) 由修正后的小波系数通过小波逆变换得到去噪后的信号。

2 仿真结果及分析

2.1 仿真结果

本文采用来源于MIT-BIH数据库的心电数据作为仿真对象, 截取了其中一段比较干净的心电信号进行试验，心电数据采样频率为360Hz，取信号长度(即采样点个数) N=2048。为了清晰地观察和评价小波变换的去噪效果，在该段心电信号上叠加了频率为50Hz和0.5Hz的两个正弦信号分别模拟工频噪声和基线漂移，又叠加了随机白噪声来模拟肌电噪声及其它噪声的综合特性，含噪心电信号的表达式可用下式表示：

y(n)=f(n)+0.02sin(100nπ/fs)+0.4sin(n/fs)+0.18wh(n)

其中：y(n)为叠加噪声后的心电信号，f(n)为干净的心电信号，wh(n)为随机产生的高斯白噪声（图1是原始心电信号，图2是加噪后的信号）。利用MATLAB小波工具箱[8]，采用smys小波对含噪心电信号y(n)进行8尺度分解，将含噪心电信号分解到不同频带内，图3是含噪心电信号分解后各尺度上的小波系数和尺度系数。从图3中可以看出,基线漂移在第8尺度上有明显的体现，这是因为基线漂移的频率很低，变化趋势缓慢，几乎没有奇异点存在，进行小波分解后在绝大多数尺度上的小波系数幅度几乎都为零；肌电干扰在第1、2尺度上最为集中；工频干扰主要集中在第2尺度上。最后根据软阈值法，利用上述自适应阈值法设定的阈值去调整小波变换系数，去除心电信号中的各种噪声，最后对调整后的小波变换系数进行逆变换，这样就得到了除噪后的信号数据，重建后的仿真图如图4所示。

图 1 MIT-BIH数据库原始心电信号

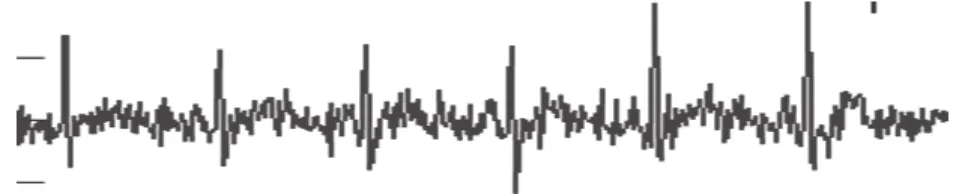
图 2 加噪后心电信号

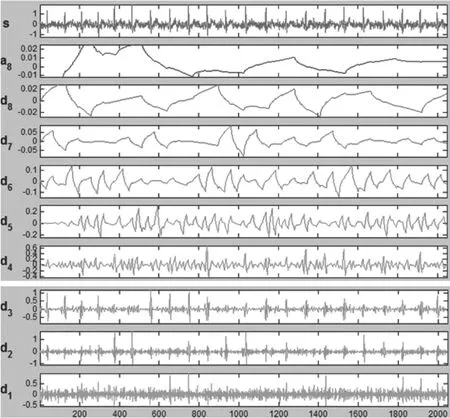
图 3 心电信号的8尺度小波分解

图4 除噪后心电信号

2.2 仿真结果分析[9-12]

通过实验可知：

(1)与传统滤波器法相比，小波变换去噪法应用起来更方便，它本质上相当于一个具有多个通道的带通滤波器，而传统滤波器法对于不同截止频率的信号，需要设计不同截止频率的滤波器才能实现。

(2) 小波变换去噪法原理简单，可以在一定程度上同时去除心电信号中的工频噪声、基线漂移和肌电噪声等多种噪声，是一种具有一定优势的去噪算法。

(3) 心电信号中的基线漂移是变化较缓慢的分量，在小波变换中显示在较大尺度上，该尺度包含的有用信号的信息通常较少，所以一般重构时直接将这一尺度的逼近信号分量置零，可有效地去除基线漂移。

(4)小波变换去噪法对于噪声与信号的频带没有重叠的情况下，去噪效果非常有效；对于有用信号和噪声的频带相互重叠的情况，效果就不太理想。从图4重建的心电信号中可以看出：由于工频干扰和肌电干扰的频带与心电信号频带重合，进行小波分解时噪声遍布在绝大多数尺度上，不能彻底地将它们完全从心电信号中分离出来。

(5)本文通过对小波变换去噪法的实验可知：小波变换去噪法在保持心电信号基本特征的情况下，可有效地抑制心电信号的噪声，而且降低了去噪算法的复杂度。选用的自适应阈值具有自适应性，适合心电信号去噪的处理，与传统的心电信号去噪方法相比有明显的优越性。

[1] 曹细武,邓亲恺.心电图各波的频率分析[J].中国医学物理学杂志,2002,18(1):46-48.

[2] 邓亲恺.现代医学仪器设计[M].北京:科学出版社,2004:161.

[3] 胡广书.现代信号处理教程[M].北京:清华大学出版社,2004: 397-405.

[4] Brij N Singh Arvind K Tiwari Optimal seletion of wavelet basis function applied to ECG signal denoising[J].Digital Signal Processing,2006(16):275-287.

[5] Willis J Tompkins.Biomedical Digital Signal Processing[M].New Jersey Premice Hall,1993:271-272.

[6] 张泾周,寿国法,戴冠中.基于小波变换的心电信号噪声处理[J].西北工业大学学报,2005,23(2):11-14.

[7] 薛涛.小波阈值去噪技术在ECG信号处理中的应用[J].微计算机信息,2007,23(2):306-308.

[8] 葛哲学,陈仲生.Matlab时频分析技术及其应用[M].北京:人民邮电出版社,2006:180-235.

[9] 季忠,秦树人.微弱生物医学信号特征提取的原理与实现[M].北京:科学出版社,2007:64.

[10] 胡俊峰,等.基于小波变换的CT/SPE CT图像融合最佳层数选取[J].中国医疗设备,2009(3):10-12.

[11] 陆英北,张增芳.基于小波变换的心电信号基线矫正方法[J].北京生物医学工程, 2000,19(4):235-239.

[12] 郭彤颖,吴成东,曲道奎.小波变换理论应用进展[J].信息与控制,2004(1):67-71.

ECG Denoising Method and Simulation Based on Wavelet Transform

XI Chao-ling,QIU Lian-kui
Telecommunication College,Henan University of Science and Technology, Luoyang Henan 471003, China

R319

A

10.3969/j.issn.1674-1633.2010.11.007

1674-1633(2010)11-0019-03

2010-04-29

2010-05-16

本文作者：席朝岭，在读研究生。

邱联奎，副教授，硕士生导师。

作者邮箱：hnyzxcla@163.com

Abstract:In order to remove all kinds of noise in the ECG,in this paper,we use the wavelet adaptive threshold denoising method which takes use of the multi-resolution feature of the wavelet transform.ECG has been reconstructed using of the adjusted coefficients.Through MIT-BIH database ECG simulation and verification,we can effectively eliminates noise.This method has obvious advantages compared with the conventional filter denoising.

Key words:ECG;wavelet-transform;ECG simulation;denoising