一个含有 2n个非零元的极小谱任意符号模式✳

王燕玲,邵燕灵

(中北大学 理学院,山西 太原 030051)

0 引 言

符号模式矩阵是一类特殊的矩阵,其元素均取自于集合 {+,-,0}.若 B=(bij)是给定的一个实矩阵,由 bij的符号为元素所组成的矩阵称为 B的符号模式矩阵,记为 sgn B.若给定一个 n阶符号模式A=[aij],则 A的定性矩阵类定义为

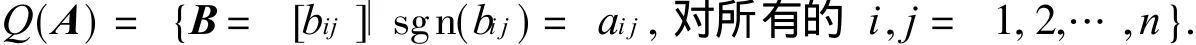
若 A= [aij]和 B= [bij]为两个同阶符号模式,当 aij≠0时,bij=aij,B为 A的母模式;当 aij=0时,bij=0,B为 A的子模式.符号模式 A既是它本身的母模式又是它的子模式.符号模式 A的不是它本身的母(子 )模式,为 A的真母(子 )模式.

对 n阶符号模式 A,如果存在一个实矩阵 B∈Q(A)且对某个正整数 K,有 BK=0,则称 A蕴含幂零,B为幂零矩阵.如果对任意 n阶首 1实多项式 r(x),在符号模式 A的定性矩阵类 Q(A)中存在一个矩阵 B,使得 B的特征多项式为 fB(x)=r(x),则称 A是谱任意符号模式.如果谱任意模式 A的任意一个真子模式都不是谱任意的,则称 A为极小谱任意符号模式.如果 A是谱任意的,则它一定是蕴含幂零的.对一个 n阶符号模式 A,若任一矩阵 B∈Q(A)是非奇异的,则 A是符号非奇异的;若每一个矩阵B∈Q(A)是奇异的,则 A是符号奇异的.

符号模式的谱任意最早在文献 [1]中提出,并给出了证明符号模式及其所有母模式是谱任意的幂零-雅可比方法,第一个 n≥2阶谱任意符号模式在文献 [2]中提出.后来,文献 [3-8]等文章分别给出了一些谱任意模式.

1 有关结论

设 x 1,… ,xn是实变量 ,T i=T i(x 1,… ,xn)是关于变量 x 1,… ,xn的实函数 (其中 i=1,2,… ,n),且 T i对任意 xj(j=1,2,…,n)均有连续偏导数.定义函数 T1,…,Tn对变量 x1,… ,xn的雅可比矩阵为 J=

引理 1[1]A是一个 n阶符号模式,若 A蕴含幂零矩阵 B,且 B中至少含有 n个非零元 bi1j1,bi2j2,…,binjn.把 B中的这 n个非零元用变量 x 1,…,xn代替后所得的矩阵记为 X,设 X的特征多项式为

本文研究如下类型的 n阶(n≥6)符号模式

任取实矩阵 A∈Q(K),设 A有如下形式

式中:ai＞ 0(i=1,2,… ,n).引理 2 设 n阶矩阵 A的特征多项式为

令a0=1,则

证明 (a)

加到第 1列,使第 1列除第 n行元素外,其余元素均为 0,然后按第 1列展开,可得

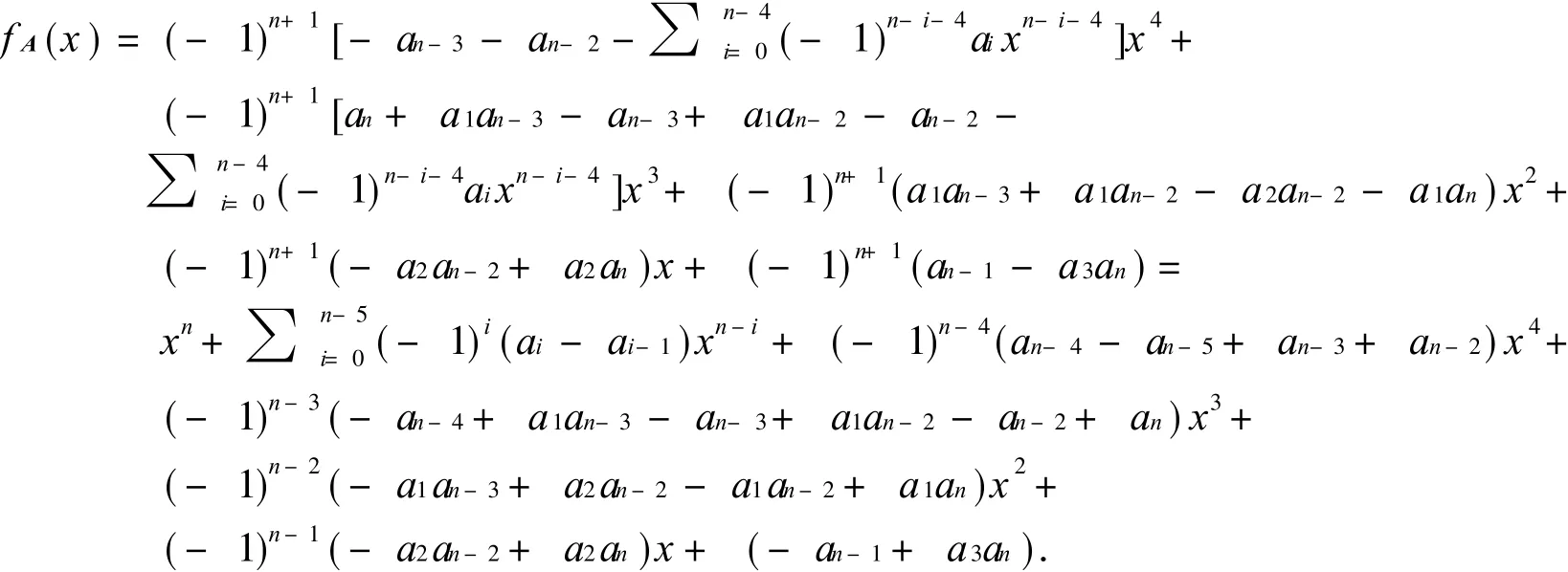
因此 (a)成立.

引理得证.

引理 3 当 n≥6时,K蕴含幂零.证明 假定 T i=0(i=1,2,… ,n),由引理 2的 (a)可得 ai=1(i=1,2,… ,n-5),aj=(j=n-4,n-3,… ,n),故当 a1=a2=…=an-5=1,an-4=an-3=…=an=时,A∈ Q(K)为幂零矩阵,引理得证.

2 主要结果

定理 1 当 n≥6时,K及其母模式是谱任意的.

证明 由引理 1,引理 2及引理 3可知定理得证.

定理 2 当 n≥6时,K为极小谱任意模式.

证明 当 n≥6时,令 T=[tij]是 K的真子模式,且 T是谱任意模式.① tn-1,n-1≠0,否则 T的迹为正,与 T是谱任意模式矛盾.② ti,i+1≠0(i=4,… ,n-3),tn-1,n≠0,否则 T是符号奇异的,与 T是谱任意模式矛盾.③ t1,2≠0,t2,3≠0,t3,4≠0,tn-2,n-1≠0,否则 T是符号奇异或符号非奇异的,与 T是谱任意模式矛盾.④ ti,1≠0(i=1,2,… ,n),否则由引理 2的 (a)知 T i≠0,与 T是谱任意模式矛盾.定理得证.

[1]Drew J H,Johnson C R.Spectrally arbitrary patterns[J].Linear Algebra Application,2000,308:121-137.

[2]McDonald J J.On the spectra of striped sign patterns[J].Linear Multilinear Algebra,2003,51:39-48.

[3]Cavers M S.On determining minimal spectrally arbitrary patterns[J].Elec.J.Linear Algebra,2005,13:240-248.

[4]Britz T.Minimal spectrally arbitrary sign patterns[J].SIAM J.Matrix Anal.Appl.,2004,26:257-271.

[5]Gao Yubin,Shao Yanling.A spectrally arbitrary pattern[J].Advances in Mathematics,2006,35:551-555.

[6]Gao Yubin,Shao Yanling,Li Zhongshan.A note on spectrally arbitrary sign patterns[J].JP Journal of Algebra,Number Theory and Applications,2008,11:15-35.

[7]McDonald J J.Spectrally arbitrary ray patterns[J].Linear Algebra and Its Applications,2008,429:727-734.

[8]Li Shoucang.Two new classes of spectrally arbitrary sign patterns[J].Ars Combinatoria,2009,90:209-220.