图像重建的统计自适应子集算法✳

孔慧华,潘晋孝

(中北大学 理学院,山西 太原 030051)

图像重建算法主要分为两大类,一类是滤波反投影算法,以傅里叶切片定理为基础,能够用快速傅里叶变换,既快速又可信;然而,滤波反投影要求数据是完全的,受噪声影响也较大.另一类是迭代重建算法,它适合于各种几何学并允许从不完全投影数据和噪声投影数据重建,能够减少金属伪像,更好地处理有限角度的断层成像.常用的迭代算法有 ART[1],SART[2],Cimmino’s method[3],DWE和CAV[4-5]等.但由于迭代算法重建速度慢,严重限制了它的使用.1994年,Hudson等提出了有序子集算法(Ordered Subsets,OS)[6],大大减少了重建时间,加快了迭代重建的速度.虽然增加子集的数目可以加速迭代收敛,然而子集个数太多会由于子集内缺少统计信息而导致图像质量下降[7].本文提出了一种基于统计理论的子集划分方法,既能够加速收敛又能保证每个子集内含有充分的统计信息.

1 背景知识

代数重建算法是将连续的图像离散化,从而转化成代数方程组

的求解问题.其中,R=(rij)I×J为系统矩阵(通常是一个大型非负稀疏矩阵);y=(y1,y2,…,yl)T为测量投影;x=(x1,x2,…,xJ)T为未知图像向量.图像重建问题就是从测量投影 y重建未知图像 x.由于系统矩阵的病态性,测量数据 y的噪声污染性以及在实际应用中数据的巨大维数,对该问题直接求解显然是不可行的.而迭代算法由于在上述问题中的优越性,被发展成了有效的图像重建算法.

解方程 (1)的大部分迭代算法可以被写为下面的形式[8]

式中:V和W分别是两个正定对角矩阵,阶数分别为 J,I;λl是松弛因子.由于迭代系统 (2)在每次更新像素值时用到了观测数据 y中的所有元素,从而被称为是联合的.

近年来,式 (2)的 OS形式引起了人们的很大兴趣.设指数集合 B={1,2,… ,I}可以被分成 T个非空的不相重叠的子集

假设

设

式中:Ri是 R的第 i行;Wi是 W的第 i行对角线元素;yi是 y的第 i行元素.则式 (2)的 OS形式可以被写作[8]

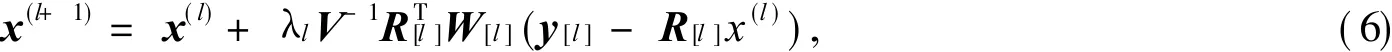
其中:[l]=l(mod T)+1对 l≥T.从 l=k T到 l=(k+ 1)T(k=0,1,2,L)的迭代过程叫做一个 OS循环,一个循环内所有的子集恰好被用到一次.当 T=1时,式 (6)还原为联合形式 (2).

通过合适地选择对角矩阵 V和 W,算法 SART,Cimmino’s,DWE,CAV都能够被写成式(2)或者式(6)的形式[8].

2 统计自适应子集算法

在使用 OS算法时,保证子集内有充分的统计信息是非常重要的,一般子集的形成要避免对噪声敏感或其它伪迹的形成.传统的 OS算法中,通常选取的子集个数 T是固定的,即每个子集内含有相同的投影数.本文提出的统计自适应子集利用统计学中的假设检验[9]方法来划分子集.首先,提出假设,建立检验统计量;然后根据给定的显著性水平T求出 H0成立时的拒绝域;最后根据样本观测值进行判断子集是否形成.

Ⅰ.提出假设

H0:子集内统计信息达到用户的要求↔H 1:子集内的统计信息还没有达到用户的要求.

Ⅱ.建立检验统计量

本文研究两个划分子集的检验统计量.第一个是对测量投影数据 yi与估计投影数据 y^i的差的平均值

式中:St,j表示像素 j的第 t个子集;m是子集 St,j内穿过像素 j的投影数目.这个统计量反映了投影数据的一定信息量,但由于它分布中的参数不容易确定,在使用这个统计量时,通常是对这个量给定一个阈值,满足接受,不满足则拒绝.

第二个检验统计量的定义为

以定理的形式给出该统计量分布.

定理 1 如果图像被认为是一个可行性图像,即统计假设 y1,y2,…,yl分别是均值为 y^1,^y2,… ,y^l的泊松采样,能够被接受[10].则

式中:St,j表示像素 j的第 t个子集;m是子集 St,j内穿过像素 j的投影数目.

证明 由于图像是可行性图像,从统计上可以得到

于是

又由于从不同的探测器测得的数据是相互独立的,根据中心极限定理可得结论.证毕.

由该定理可以看出,当 m充分大时,第二个统计量服从标准正态分布.

Ⅲ.根据样本值进行检验

这里的检验是在重建过程中进行的,其步骤如下:①初始化图像 x(0).②计算第 i根射线的投影值.③计算经过第 i根射线的每个像素 j的统计量的值,并判断是否落在拒绝域内.若检验通过,则接受假设,像素 j的子集 St,j形成,对目前的 x j更新;否则拒绝假设,子集不形成,像素值不被更新.④重复步骤②,③直到 I个方程都完成,这时得到的各 x j值叫做完成了第一轮迭代.一般要经过 K轮迭代,直到取得符合收敛要求的结果为止.

设 l=T(1)+ T(2)+…+T(n)+tn-1,其中 tn+1是第 n+1次迭代的第 t个子集,则该算法的迭代公式为

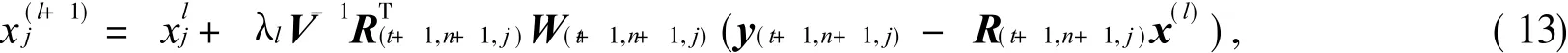
与有序子集的迭代公式非常相似.其中,Vj为矩阵 V第 j行对角线上的元素;(t+1,n+1,j)表示第 n+1次迭代第 j个元素的第 t+1个子集.

3 实验结果与分析

实验中,将统计自适应子集 (Statistical Adaptive Ordered Subsets,SAOS)方法应用在 SART上,得到 SAOS-SART.本文将将采用第一个检验统计量的 SAOS-SART表示为 SAOS-SART-A,用第二个检验统计量的 SAOS-SART表示为 SAOS-SART-B.重建公式如下

式中:x(jl+1)是像素 j对当前子集 t+ 1的更新值;x(jl)是像素 j更新前的值.

该公式只是对 OS-SART[11]的重建公式进行了很小的改动.

为了检验统计自适应子集算法的可执行性,将 OS-SART,SAOS-SART-A和 SAOS-SART-B的公式用 C语言在计算机 (RAM:1 G;CPU:P1.86 GHz)上进行编码.

重建的收敛率用归一化判据 d衡量

式中:xi和 x^i分别表示原图像和重建图像中第 i个像素的灰度;表示原始图像的平均灰度.归一化均方距离判据越小,表明重建图像与原始图像越接近,重建图像的质量越好.

实验选取 Shepp-Logan切片作为仿真对象,大小为 256×256像素,灰度级为 0～ 255.投影采样间隔为 1°,采样区域为0°～ 180°.每个投影方向有 256个探测器.实验中分别用无噪声投影数据和加了投影总数 5%的泊松噪声的投影数据进行重建.实验中的参数设置如下:OS-SART的子集数为 45,SAOSSART-A的阈值为 5,SAOS-SART-B的显著性水平为 0.4,即置信水平为 0.6.所有算法中的松弛参数均为 0.5.

图1显示了以上 3种算法从无噪声投影数据迭代 10次的归一化距离判据.从图1中可以看到,SAOS-SART的收敛速度明显较 OS-SART快,而 SAOS-SART-A和 SAOS-SART-B有着几乎相同的收敛速度.

图2给出了以上 3种方法从无噪声投影数据迭代 3次的重建切片.

图1 无噪声投影数据重建切片的归一化距离判据Fig.1 Normalized root criteria for slice reconstruction from noiseless projection data

图2 无噪声投影数据迭代 3次后的 Shepp-Logan切片Fig.2 Reconstruction of the Shepp-Logan slice from noiseless projection data after 3 iterations

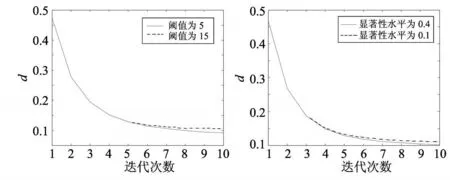
图3 不同阈值和显著性水平下的归一化距离判据Fig.3 Normalized root criteria with different thresholds and different significant lev els

图4 噪声投影数据重建切片的归一化距离判据Fig.4 Normalized root criteria for slice reconstruction from noisy projection data

在统计自适应子集算法中,阈值和显著性水平对重建速度是有影响的.一般来说,阈值越小或者显著性水平越大(置信水平越小),收敛速度越快;反之,则收敛速度慢.图3给出了不同阈值和显著性水平下的归一化距离判据.由图3可以看出,在前几次迭代时,不同的阈值和显著性水平对算法的影响非常小,这是因为显著性水平大(置信水平小),子集内的统计信息量小,即子集内所包含的投影数较少(子集数目较大),图像更新次数多;而当显著性水平小(置信水平大)时,子集内的统计信息大,弥补了图像更新次数少这一缺点.但随着迭代次数的增加,显著性水平大,更新次数多的优势就越来越明显了.

图4显示了以上 3种算法从噪声投影数据迭代 10次的归一化距离判据,图5给出了以上 3种方法从噪声投影数据迭代 3次的重建切片.

图5 噪声投影数据迭代 3次后的 Shepp-Logan切片Fig.5 Reconstruction of the Shepp-Logan slice from noisy projection data after 3 iterations

4 结 论

本文提出了一种基于假设检验的统计自适应子集算法,该方法每次迭代时可以对每个像素动态地生成子集,虽然每个子集的大小(即子集内含投影的数目)不一样,但子集内的统计信息是相同的.本文还提出了两个生成子集的统计量,第一个统计量形式简单,适用于各种图像;第二个统计量统计意义明确,却只适用于可行性图像,重建速度可通过调节阈值和显著性水平来控制.由实验结果可以看出,阈值为5的 SAOS-SART-A和显著性水平为 0.4的 SAOS-SART-B收敛速度是几乎相当的.

在实验的过程中,还发现了一个有趣的现象,算法在前期迭代中对含有噪声的投影数据反而会得到较小的归一化距离判据,作者认为这可以从统计的角度去理解.在统计中,方差即信息量,方差大即信息量大,而含有噪声的投影数据的方差是较大的,当然随着迭代次数的增加,这种信息量的影响会逐渐变成负面的.

[1]Gordon R,Bender R,Herman G T.Algebraic reconstruction techniques(ART)for three-dimensional electron microscopy and X-ray photography[J].Journal of Theoretical Biology,1970,29(3):471-481.

[2]Andersen A H,Kak A C.Simultaneous algebraic reconstruction technique(SART):A superior implementation of the ART algorithm[J].Utrason.Ima.,1984,6:81-94.

[3]Cimmino G.Calcolo approssimato per le soluzioni dei sistemi di equazioni lineari[J].Ricerca Sci.Ⅱ,1938,9:326-333.

[4]Censor Y,Elfving T.Blockalgorithms with diagonally scaled oblique projections for the linear feasibility problem[J].SIAM J.Matrix Anal.Applicat.,2002,24:40-58.

[5]Censor Y,Gordon D,Gordon R.Component averaging:an efficient iterative parallel algorithm for largeand sparse unstructured problems[J].Parallel Computing,2001,27:777-808.

[6]Hudson H M,Larkin R S.Accelerated image reconstruction using ordered subset of projection data[J].IEEE Transactions on Medical Imaging,1994,13(4):601-609.

[7]Kadrmas D J.Statistically regulated and adaptive EM reconstruction for emission computed tomography[J].IEEE Trans.on Nucl.Sci.,2001,48(3):790-798.

[8]Jiang M,Wang G.Convergence studies on iterative algorithms for image reconstruction[J].IEEE Trans.on Medical Imaging,2003,22:569-579.

[9]盛骤,谢世千.概率论与数理统计[M].第 3版.北京:高等教育出版社,2003:213-231.

[10]Llacer J,Veklerov E.Feasible image and practical stopping rules for iterative algorithms in emission tomography[J].IEEE Trans.Med.Imag.,1989,8(2):186-192.

[11]Wang G,Jiang M.Ordered-subset simultaneous algebraic reconstruction techniques(OS-SART)[J].Journal of XRay Science and Technology,2004,12:169-177.