食品欧姆加热过程中不同电极形状的温度场分布的数值模拟

姜 欣,李 琳,田 婷,沈五雄,周家华

(1.华南理工大学轻工与食品学院,广东广州 510641;2.华南农业大学食品学院,广东广州 510642)

食品欧姆加热过程中不同电极形状的温度场分布的数值模拟

姜 欣1,李 琳1,田 婷2,沈五雄2,周家华2

(1.华南理工大学轻工与食品学院,广东广州 510641;2.华南农业大学食品学院,广东广州 510642)

为了了解 5种不同电极板形状对食品欧姆加热中物料的温度场分布及加热效率的影响,建立了不同电极形状的欧姆加热三维模型,利用有限元的方法求解欧姆加热过程中模型的温度场和电场方程,模拟分析了矩形、圆形以及弧形电极的欧姆加热过程中的温度分布.结果表明:食品的欧姆加热过程中温度场的分布与电极的形状有很大的关系,弧形电极的欧姆加热过程中,电流密度的分布与电极的弧度有关,电极的曲率越大,电场线越密集,电势梯度增大,加热过程中温度场分布越不均匀;矩形与圆形电极的欧姆加热效果相同,其电场分布及加热效率都一致.

欧姆加热;电极形状;数学模型;温度场

0 前言

为了达到食品安全保藏的目的,热加工是一种普遍采用的处理方法,在食品工业中占有重要地位.传统的热加工处理主要以热水或者蒸汽作为加热介质对食品物料进行传热而达到加热的目的,这种方法对于单一流体的连续加热是简单易行而且有效的,但是对于含颗粒流体食品的连续加热,却存在明显的缺陷:当颗粒中心通过热传导达到杀菌所需的温度时,食品物料其他部分往往处于过热的环境中,从而导致食品营养和感官品质的降低,限制了可加工颗粒的大小.欧姆加热,亦叫通电加热、电阻加热、电加热等,作为一种替代技术在含颗粒流体食品的连续加热方面引起了广泛的关注,其原理是将电流通过食品物料,由于物料本身存在电阻抗性,根据欧姆定律,电能将直接转化为热能,而达到加热的目的,是对整个食品的同步加热,能够对食品物料进行高温短时处理,最大限度地保障食品品质.因而欧姆加热是一种很有前途的食品加热技术,在食品的加工处理过程中具有广泛的应用前景,可用于食品物料的烫漂、解冻、发酵和巴氏杀菌等方面[1-3].与传统的热传导加热相比,欧姆加热杀菌对产品本身的结构、营养、蒸发脱水以及口感的影响更小[4].Li ma等[5]的研究表明欧姆加热还可以提高一些水果和蔬菜的干燥速率和提取率.

欧姆加热过程中,物料的产热率等于电场强度的平方和电导率的乘积[6]:

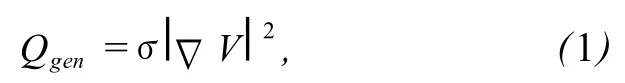
式中:Qgen为产热率电场强度的模,V/m;σ为电导率,S/m.

Palaniappan和 Sastry[7]研究表明电导率与温度成一次线性方程.当物料一定且材料性质均匀时,由式 (1)可看出,产热率由电场强度所决定,在均匀电场中,电场处处相等,物料各部分的产热均匀,温度场也随之而均匀;不均匀电场中,其电场的分布将决定温度场的分布.

欧姆加热过程物料的温度分布是否均匀,将直接影响加热过程的控制,了解物料的温度分布是保证加热杀菌食品的安全的关键.通过数学模型的模拟分析,不仅可以很直观地了解欧姆加热过程中温度的分布情况,而且可以节省大量的时间和成本.W.R.Fu和 C.C.Hsieh[3]运用有限元软件(ANSYS)模拟矩形块状物料在间歇式欧姆加热装置中加热过程的温度分布,并进行了试验验证.Xiaofei Ye和 Roger Ruan[8]运用有限元的方法模拟了含颗粒的流体食品的欧姆加热过程,同时对模拟预测的结果利用MR I温度测定法进行了验证,数学模型中考虑了电热转化效率提高了模型预测的准确性.S.Salengke和 S.K.Sastry[9]模拟了两种极端条件下的固液两相混合物料的欧姆加热过程,采用了回路电路模拟的原理,把固液混合物看成由一系列电阻组成的混联电路.F.Marra等[10]研究了欧姆加热过程中传热对物料温度场的影响并进行了试验验证.这些模型可以直观准确地观察到食品内温度场的分布,但是主要都集中在物料材料属性对温度场的影响,而不同电极形状的电场分布对温度场的影响却少见报道.而实践中,物料的形状往往不规则,对于特别形状的大宗物料的加热,可能需要设计与之相适应的电场分布来保证加热的均匀性.

因此,作者建立了矩形、圆形的平板电极和弧形电极的欧姆加热过程三维模型,利用有限元方法对不同电极形状的欧姆加热过程中物料的电场及温度场分布进行数值模拟.

1 模型建立

1.1 欧姆加热物理模型的建立

1.1.1 物料的材料参数

物料模型物为固体,且体积保持不变,为8.811×10-4m3,物料的材料参数如表1所示,电导率为温度的线性函数.

表1 物料的参数

1.1.2 电极板的形状及物料的几何模型

模拟中,采用 5种不同的电极板形状,各电极板的面积相等,物料总的加热体积一定.图 1表示5种电极板条件下欧姆加热的物理模型示意图.

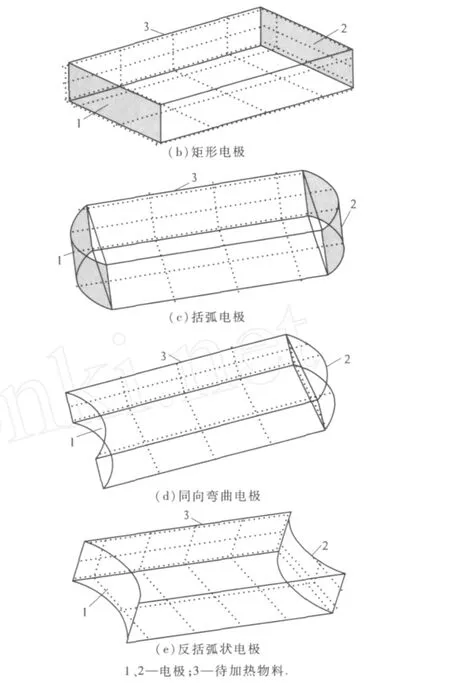
图1 不同形状的电极的欧姆加热几何模型

1.2 数学模型

1.2.1 模型假设

1)物料的热传导率、密度、比热在加热过程中恒定.

2)加热过程中体系保温,物料与容器外壁的热交换量为零.

1.2.2 温度场控制方程

在欧姆加热过程中,发生了热的传递现象.此现象由含热源的瞬态热传导微分方程控制:

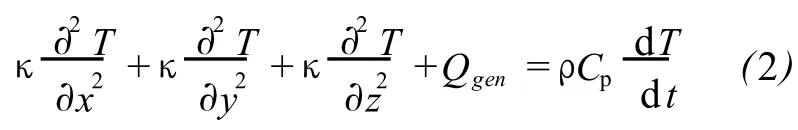
式中:T为物料内部温度,K;t为物料加热的时间,s;κ为热传导率,W/(m·K);Cp为物料的比热容,J/(kg·K);ρ为物料的密度,kg/m3;Qgen为产热率,W/m3,由公式 (1)所决定.

欧姆加热过程中的电位分布控制方程为:

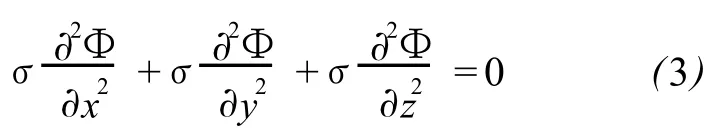
式中:Φ为电场强度的标量.

2 数值求解的方法

2.1 初始条件和边界条件

求解传热偏微分方程 (2),需要给定方程的初始条件和边界条件,而电场分布控制方程 (3)属于稳态方程,只需给定其边界条件即可.

在方程式 (2)中,假设物料的初始温度为 298 K,加热过程中物料向环境的热量损失为 0,即边界条件为绝热.方程 (3)的边界条件:图 1物料模型中标为电极的两端表示物料与电极的接触面,其中一面设电压为 220 V,一面设电压为 0 V表示接地,其他各面设为绝缘条件.

2.2 网格的划分及求解

利用有限元方法之前,首先对模拟的对象进行有限元网格划分,由于在不同的计算区域有不同的尺寸,所以划分网格要按照不同的尺寸来对不同的区域进行网格尺寸的控制.本研究采用自适应网格划分的形式,各种电极形状的网格参数统计如表2所示.

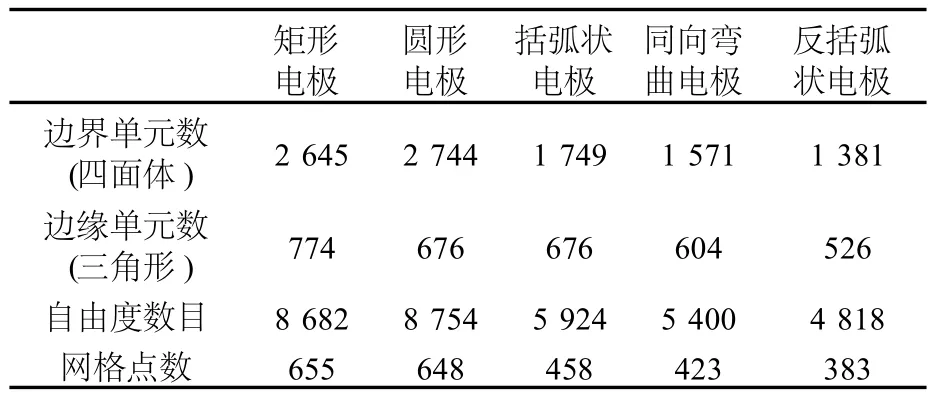
表2 不同电极形状中网格数的统计

欧姆加热过程中涉及到传热和电场方程,在设定初始条件和边界条件后,通过有限元分析方法进行求解.在欧姆加热过程中的每个时间段,利用隐式时间求解参数通过牛顿迭代来求解上述非线性系统方程.

3 结果与分析

3.1 不同电极形状中的温度场分布

在物料的初始温度为 298 K,电极一面加上220 V电压,一面接地,物料加热 270 s后,其他条件一致的情况下,选取高度 Z=0.022 5 m时,对不同电极欧姆加热中物料的几何截面温度分布场进行分析和讨论.

如图 2所示,从模拟的温度场分布图上可以看出在整个加热过程中,圆形平面电极和矩形平面电极的温度分布均匀一致,热点和冷点温度之间的温差为 0 K.括弧状电极、反括弧状电极及同向弯曲电极的温度分布相对不那么均匀,且热点温度和冷点温度出现的位置基本一致,都在电极板与流场接触的拐角处出现温度的最值.三者的热点温度和冷点温度差分别为:100 K、34 K、85 K.

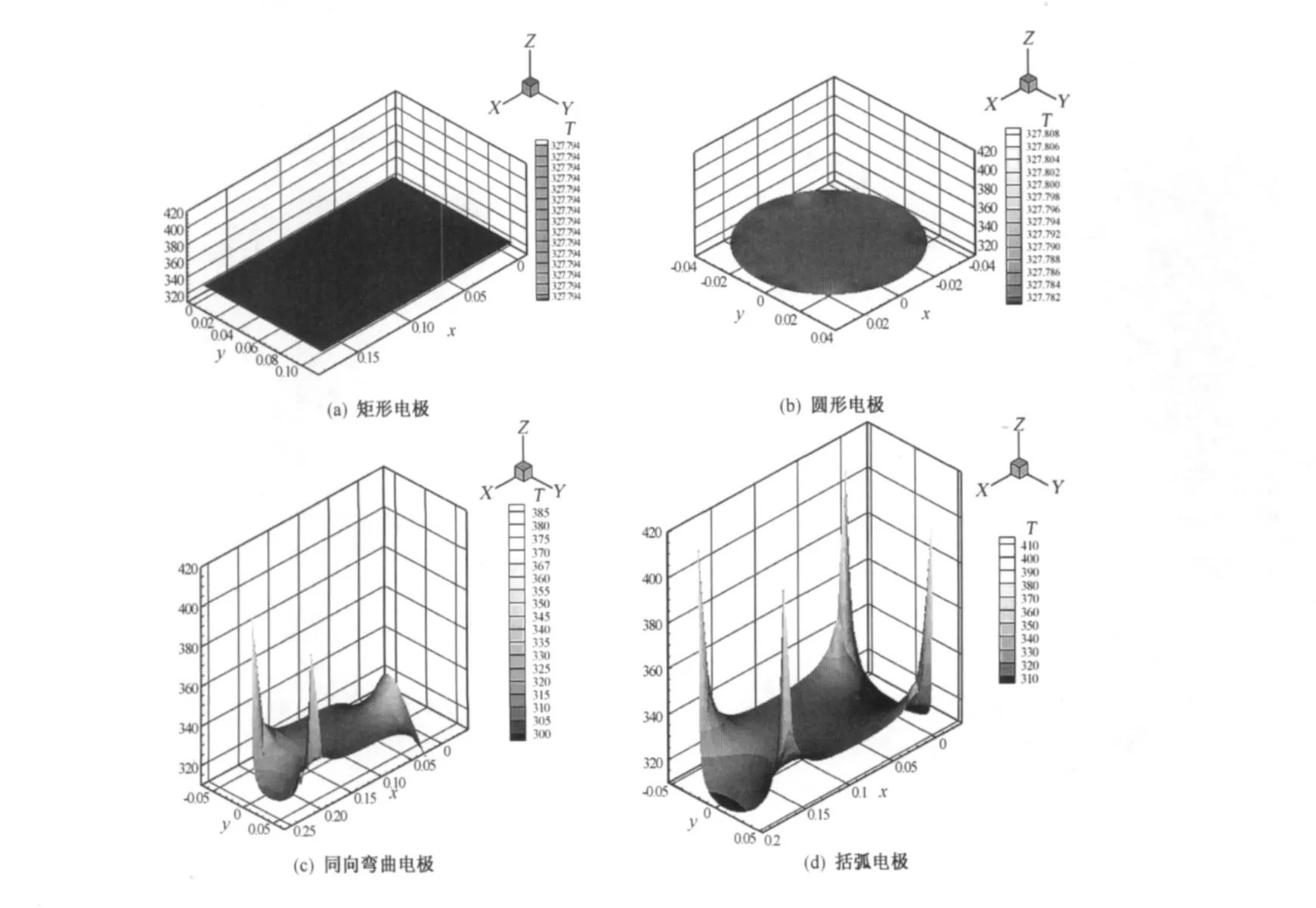
图2 加热 270 s后不同电极的欧姆加热内物料温度分布

由于电流密度的分布与电极的弧度有关,电极的曲率越大,电场线越密集,电势梯度增大,加热过程中温度场分布越不均匀,我们也研究分析了欧姆加热过程中相应截面的电流密度分布(图 3).

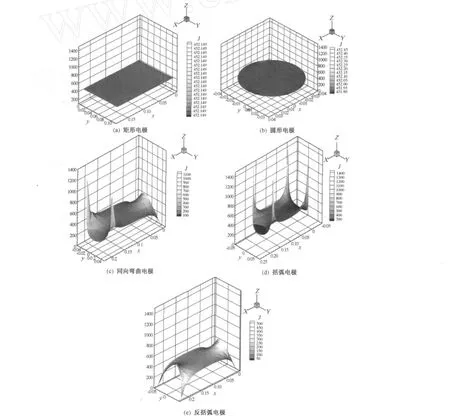
图3 加热 270 s后不同电极的欧姆加热内物料电流密度分布

由图 3可知,电极形状不同,电流密度分布也不同.矩形和圆形电极上电流密度的分布都很均匀且大小相等,其他 3种形状的电极密度分布都呈梯度分布.电流密度在电极与流场板接触面的拐角处的值呈现最大值或最小值,最大可达到1 410 A/m2,最小可达到 50 A/m2.这可能是由于两电极板间的距离不同.在模拟过程中我们保持了相同的电极面积及相同的物料体积,使得电极板间的距离发生变化 (矩形和圆形电极之间的距离大小相等),这是决定电场强度大小的关键因素.与同向电极和括弧电极相接触处的流场处的距离较处于相对位置的电极的距离近,故其附近出现最大峰值.而反括弧则相反,这与 Shames等[11-13]的研究结果一致.

综合考虑温度和电流密度分布场可知,不同的电极形状上的电流密度分布趋势与温度分布趋势一致,温度分布越高的地方,电流密度的分布也越高,反之也一样.这也表明电极板的形状对温度的分布有影响.

3.2 物料加热效率的分析

欧姆加热的优点是加热速率快且加热比较平均,为了研究各电极形状对食品物料的加热效率,分析了欧姆加热过程中物料平均温度的分布(图4).

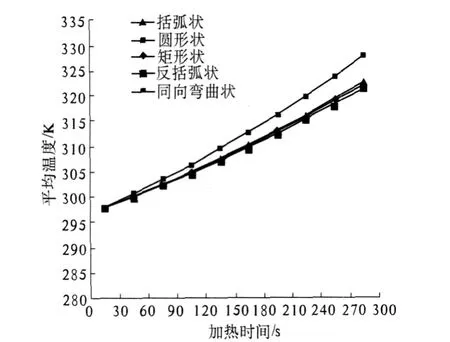
图4 各电极形状对物料加热效率的影响

由图 4可知,在欧姆加热过程中,圆形电极和矩形电极对物料的加热效率最高,且加热效率相同.其他 3种电极的加热效率略低于圆形和矩形电极,相差不大.各种电极的加热速率呈增大趋势,这与物料的电导率有关,而电导率是与温度有关的函数,随着加热时间的延长,物料的温度逐渐升高,物料的电导率也逐渐增大,导致加热速率增大.

4 结论

通过有限元分析不同电极形状欧姆加热温度场分布的数值模拟,主要得出以下几点结论:

1)矩形电极和圆形电极的温度分布均匀一致.其他 3种形状电极的温度分布都不均匀,最高温度为 410 K,最低温度为 300 K.

2)矩形电极和圆形电极的电流密度分布均匀一致,其他 3种形状的电极在与流场接触的拐角处出现最值.

3)综合考虑,矩形和圆形电极板加热效率最高.

实践中,对于形状不规则食品物料,特定的欧姆加热设备往往难以满足物料的加热需求.根据食品物料的形状和配方选用适用形状的加热电极,对于解决欧姆加热过程中物料产热率不均匀的问题具有积极的意义.

[1] 周亚军,殷涌光,刘微,等.食品欧姆加热技术的原理及研究进展 [J].吉林大学学报:工学版,2004(2):324-329.

[2] ZhangL,Fryer P J.Models for the electrical heating of solid-liquid food mixtures[J].Chem Eng Sci,1993,48:633-642.

[3] FuW R,Hsieh C C.Simulation and verification of two-dimensionalohmic heating in static system[J].J Food Sci,1999,64:946-949.

[4] RahmanM S.Handbook of Food Preservation[M].New York:Marcel,1999:521-532.

[5] Lima Marybeth,Heskitt B F,Sastry S K.The effect of frequency and wave fo rm on the electric conductivity temperature profiles of turnip tissue[J].Journal of Food Process Engineering,1999,22:41-54.

[6] Sastry S K,Palaniappan S.Mathematical modeling and experimental studies on ohmic heating of liquid-particle mixtures in a static heater[J].Food Proc Eng,1992,15:241-261.

[7] Palaniappan S,Sastry S K.Electrical conductivities ofselected solid foods during ohmic heating[J].Journal of Food Process Engineering,1991,14:136-221.

[8] Xiaofei Yea,Roger Ruana,Paul Chen.Simulation and verification of ohmic heating in static heater usingMR I temperature mapping[J].Technol,2004,37:49-58.

[9] Salengke S,Sastry S K.Models for ohmic heating of solid-liquid mixtures unde rworst.case heating scenarios[J].Journal of Food Engineering,2007,83:337-35.

[10]Marra F,ZellM,Lyng J G.Analysis of heat transfer during ohmic processing of a solid food[J].Journalof Food Engineering,2009,91:56-63.

[11]Shames P,Sun P C,Fainman Y.Modeling and optimization of electro-optic phase modulator[J].SPIE Proc Phys Simul Opt,1996,2693:787-796.

[12]Soojin jun,Sudhir sastry.Modeling and optimization of ohmic heating of foods inside a flexible package[J].Journal of Food Process Engineering,2005,28:417-436.

[13]Sensoy I.Ohmic and moderate electric field treatment of foods:Studies on heat transfer modelling, blanching, drying, rehydration and extraction[D].Ohio State:The Ohio State University,2002.

NUMER ICAL SI MULATI ON OF TEMPERATURE FIELD D ISTR I BUTI ON DURI NG FOOD OHM IC HEATI NG BY ELECTRODESW ITH D IFFERENT SHAPES

J I ANG Xing1,L ILin1,TI AN Ting2,SHEN Wu-xiong2,ZHOU Jia-hua2
(1.College of L ight Industry and Food Sciences,South China University of Technology,Guangzhou510641,China;2.College of Food Science,South China Agricultural University,Guangzhou510642,China)

We studied the temperature field distribution and the heating efficiency ofmaterials heated by five electrode plates with different shapes during food ohmic heating process,constructed the three-di mensional ohmic heatingmodels for different electrodes,solved the temperature field equation and the electric field equation of the ohmic heatingmodels by finite elementmethods,and si mulated the temperature field distributionsof the ohmic heating process of a rectangular electrode,a round electrode and an arc-shaped electrode.The results showed that the temperature field distribution of the food ohmic heating process had a strong relation with the electrode shape;the current density distribution was related with the radian of the electrode during the ohmic heating process of the arc-shaped electrode,that is to say,the larger electrode curvature resulted in denser electric field lines,larger potential gradient and more nonunifor m temperature field distribution;and the rectangular electrode and the round electrode had the same ohmic heating effect,and the same electric field distribution and heating efficiency.

ohmic heating;electrode shape;mathematicalmodel;temperature field

TS205

B

1673-2383(2010)05-0075-06

2010-06-11

国家自然科学基金资助项目(30900990)

姜欣(1973-),女,辽宁宽甸人,讲师,博士研究生,主要从事糖类物质、药物制备和生物利用方面的研究.