测量平差中必要观测数确定的新方法

2010-09-28欧吉坤宁亚飞

测绘通报 2010年8期

关键词：个角测角方位角

宁伟,欧吉坤,宁亚飞

(1.淮海工学院测绘工程学院,江苏连云港 222005;2.中国科学院测量与地球物理研究所,湖北武汉 430077;3.山东农业大学信息科学与工程学院,山东泰安 271018)

测量平差中必要观测数确定的新方法

宁伟1,2,欧吉坤2,宁亚飞3

(1.淮海工学院测绘工程学院,江苏连云港 222005;2.中国科学院测量与地球物理研究所,湖北武汉 430077;3.山东农业大学信息科学与工程学院,山东泰安 271018)

在测量平差中,无论采用哪种平差模型,必要观测数的确定都是进行平差的关键和前提因素之一。传统的确定必要观测数的方法在较为复杂的几何模型层面上,往往存在较大的局限性。在对有关文献作进一步分析和研究的基础上,从逆向思维角度出发,得到一套根据不同的观测条件来确定必要观测数的新方法。

测量平差;必要观测数;多余观测数;联合确定

一、必要观测数的确定方法

在测量工作中,为了能及时发现错误和提高测量成果的精度,常进行多余观测,这也就产生了平差问题。在平差过程当中,通常考虑的平差模型有条件平差模型、附有参数的条件平差模型、间接平差模型和附有限制条件的间接平差模型,这些模型之间的内在联系,一些文献中已讨论许多,具体见文献[1-3]。无论采用哪种模型,其中的方程个数的确定,必须要以正确的必要观测数为前提。已有确定必要观测数的方法[4]见表 1。

表1

表中各字母含义可见文献[4],从表中可以看出：

1)水准网结构单一,形式简单,用表 1的方法完全可以应对,不再赘述;

2)除水准网外,可将几何模型大体上分为以下三类：

a.以测角网为主体的,凭借一个测角网就可以确定观测图形;

b.以测边网为主体的,凭借一个测边网就可以确定观测图形;

c.以边角网为主体的,凭借一个边角网就可以确定观测图形。

具体思路如下:首先,观察图形属于上述三类中的哪一种;接着在确定类型之后,提取图形中的已知条件和与其同一类别的条件,用表 1确定这里面的必要观测数 t1,进而由 r1=n1-t1得到相应的多余观测 r1;其次,将模型中剩余的条件拿出来逐个比对上面的条件,看是否可构建方程,若能,则该剩余条件为多余观测,此时将其视为已知条件处理。以此类推,便得这类多余观测总数,不妨用 r2表示,最后用 t=n-(r1+r2)确定必要观测数。现举例如下[5-6]:

二、实例分析

例 1 如图 1所示,现观测了 18个角 (β1～β18和 3条边 (s1,s2,s3)。

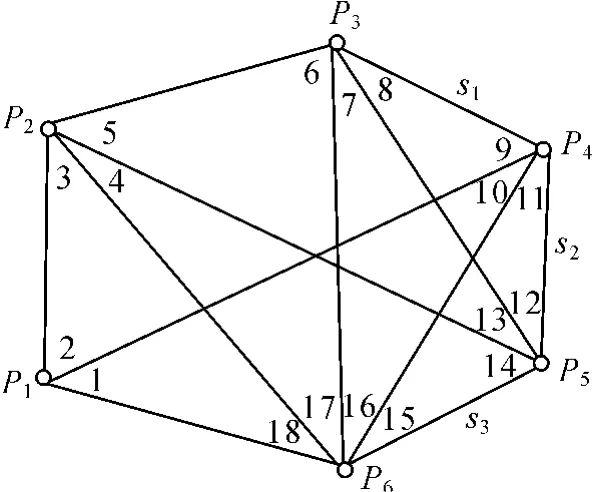
图1

分析:这显然属于第一类,即以测角为主体,根据表 1,先考虑测角网。取出这 18个角,n1=18,由t1=2p-4=2×6-4=8知 r1=n1-t1=18-8=10,下面进行逐一比对:显然剩余观测值 s1不能构造方程,s1不是多余观测,而 s2和 s1可用正弦定理构造方程,s2是多余观测;s3和 s1或 s2也能构造方程,也是多余观测,这样 r2=2,所以,t=n-(r1+r2)=21 -(10+2)=9,即为所求必要观测数。

例 2 如图 2所示,已知A、B点坐标,有 5个观测边,2个观测角。

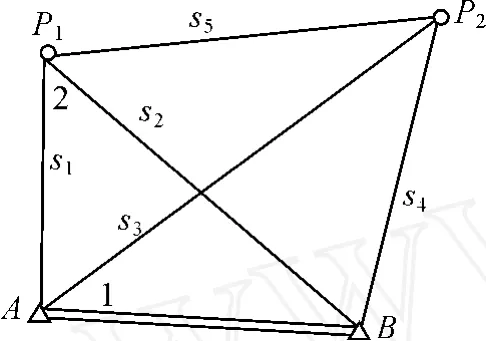
图2

分析:这应该属于第二类,即以测边为主体,取出A、B两点坐标和 5条边,易知 r1=1,显然,测角 1可用余弦定理构建方程,是多余观测,测角 2也可用余弦定理构建方程,也是多余观测,故 r2=2,所以, t=n-(r1+r2)=7-(1+2)=4。

例 3 如图 3所示,已知 3点坐标.,3个观测角,4个观测边。

图3

分析:这应该属于第三类,取出最简单的边角网,包含三条边长 s1、s2、s3和角 1、2,由表 1可知,r1=0,取出测角 3和测边 s4,显然均可建立方程,即r2=2都可,所以,t=n-(r1+r2)=7-(0+2)=5。

例 4 如图 4所示,Pi(i=1,2,…,5)为待定点, T1、T2为已知方位角,s为已知边,观测了 1～13个角度。

分析:这应该属于第一类,由表 1可知,该测角网必要观测数为 t1=2p-4=2×5-4=6,所以, r1=n-t1=13-6=7,考虑方位角 T1和 T2,显然它们和观测角 1、2、3、11、12、13可构建一方程,即 r2= 1,因此,t=n-(r1+r2)=13-(7+1)=5。

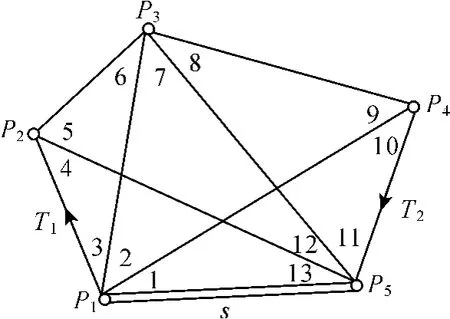
图4

例 5 如图 5所示,已知两点坐标A、B,观测了12个角,两条边 s1、s2,Pi(i=1,2,3)待定。

图5

分析:显然,这也属于第一类,由表 1可知,考虑测角网通用公式,可知 t1=2p-4=2×5-4=6, r1=n1-t1=12-6=6。下面进行比对:取出 s1,显然它与测角 1、2、5、11、12,以及已知边AB可构建一个方程,表明 s1为一个多余观测,s2和 s1也能构造一个方程,说明 s2也是一个多余观测,所以 r2=2, t=n-(r1+r2)=14-(6+2)=6。

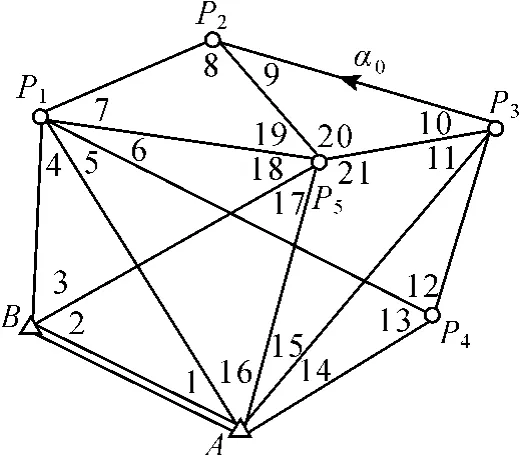
图6

例 6 如图 6所示,A、B为已知点,α0为已知方位角,Pi(i=1,2,…,5)为待定点,共观测了 21个角。分析:这属于第一类情况,考虑测角网,并利用表 1的通用公式,可求得 t1=2p-4=2×7-4=10, r1=n-t1=21-10=11,显然,由已知点坐标、观测角和已知方位角α0可建立一方程,即 r2=1,所以,t

=n-(r1+r2)=21-(11+1)=9。

例 7 如图 7所示,A、B为已知点,α0为已知方位角,s0为已知边长,Pi(i=1,2,3,4)为待定点,共观测了23个角。