Gouy-Chapman双电层模型在蒙脱石长程膨胀中应用
2010-09-28贾景超,杨庆*,2
贾 景 超, 杨 庆*,2
(1.大连理工大学土木工程学院岩土工程研究所,辽宁大连 116024;2.大连理工大学海岸和近海工程国家重点实验室,辽宁大连 116024)
0 引 言
膨胀土因为含有膨胀性矿物——蒙脱石而具有吸水膨胀特性[1].蒙脱石颗粒由相互平行的晶层叠加而成,而蒙脱石的膨胀正是源于晶层之间的吸水膨胀.晶层之间的膨胀通常分为两个阶段:第一阶段的膨胀称为晶格膨胀或水合膨胀;第二阶段的膨胀称为渗透膨胀[1、2].Zhang等[3]排除膨胀机理的影响将这两个阶段分别称为短程膨胀和长程膨胀.虽然晶层之间的膨胀大体上分为两个阶段,但是这两个阶段没有明显的分界点.奥尔芬[1]认为第一阶段的水合膨胀大约为1 nm(相当于4个水分子层),晶层间距超过1 nm之后,水合力就不重要了;而Israelachvili等[4]认为水合阶段大概相当于10个水分子层,晶层间距大约为2.5 nm.另外由于晶格膨胀涉及晶层表面的水合和晶层间离子的水合,哪种因素占支配地位至今仍未搞清楚[1、4、5].第二阶段的渗透膨胀归根结底是由同晶置换作用而导致的蒙脱石晶层内部电荷不平衡,这种不平衡表现为晶层表面带负电.为了中和这些负电荷,阳离子被吸附到晶层表面,蒙脱石吸水之后被吸附的阳离子扩散到水中,这些阳离子一方面受晶层表面负电荷的静电作用,一方面由于布朗运动而产生远离表面的扩散趋势,从而使得水中的阳离子和晶层表面的阴离子形成扩散双电层,扩散到水中的阳离子云称为扩散层,描述扩散层离子分布的模型中Gouy-Chapman双电层模型是较简单且得到广泛应用的一种[1、6、7].相互平行晶层之间的双电层相互重叠会产生双电层斥力,而众多学者已证明双电层斥力等于平行晶层的中平面处离子的渗透压和晶层外平衡溶液中相对应离子渗透压之差[8~10],从而可以结合渗透压理论和Gouy-Chapman相互作用双电层模型建立晶层间膨胀压力模型[1、8],以下简称Gouy-Chapman双电层模型.
蒙脱石晶层间的膨胀得以实现的另一个重要原因是晶层之间的联结力主要是范德华引力,这种作用力较弱,从而使得水合力和双电层斥力能够克服它而产生膨胀压力[1].
长期以来对于第二阶段的渗透膨胀或者长程膨胀的机理存在争议:一种观点认为长程膨胀源于晶层间的双电层斥力,并通过与精确的试验结果比较认为长程膨胀符合双电层理论,可以用Gouy-Chapman模型或其改进模型来描述[4、11~15];另一种观点则认为晶层间水分子的结构性排列是产生长程膨胀的决定性因素,双电层理论不能解释这种现象[3、16、17].
为澄清上述争议,本文基于Zhang等[3]的试验数据对Gouy-Chapman模型从膨胀压力-晶层间距关系以及晶层间距-电解质浓度关系两个方面对模型进行验证,并对简化Gouy-Chapman模型的适用性进行分析.
1 Gouy-Chapman模型的验证
1.1 对膨胀压力-晶层间距关系的验证
Gouy-Chapman模型包括以下几个方程[1 、6 、8 、18]:
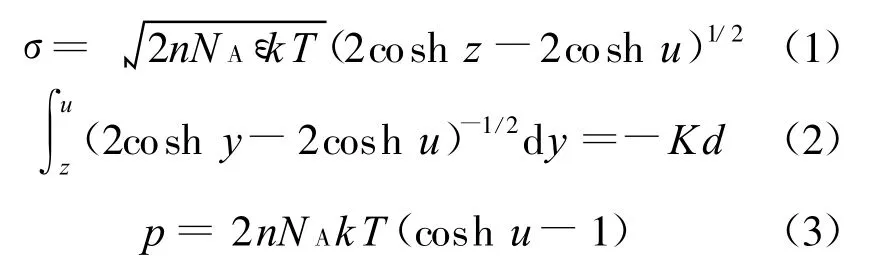
式中
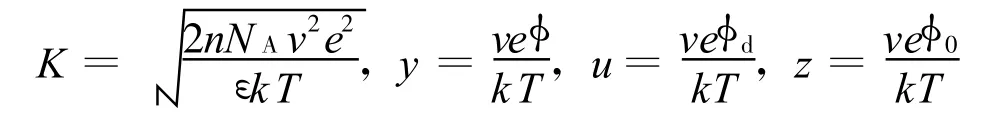
d为两平行晶层间距的一半;σ为晶层表面电荷密度(C/m2),本文σ值和Zhang等的取值都取自文献[19],为0.108;ε为电容率,等于相对电容率 εr(=80)和真空电容率ε0(=8.854×10-12C2/(N·m2))之积;k为 Boltzmann常数,1.38×10-23J/K;T为热力学温度,本文取298 K;v为离子化合价;e为单位电荷电量,1.602×10-19C;n为晶层外平衡电解质溶液物质的量浓度(mol/L);NA为阿伏伽德罗常数(1/mol);p为渗透压力或双电层斥力(kPa); 为扩散双电层中任意一处的电势; 0和 d分别为晶层表面和平行晶层中间处的电势;y、z、u分别为 、 0、 d对应的量纲一量.
在σ和n已知的情况下由晶层间距λ=2d计算渗透压力,需要知道u的值,但是由于式(2)是椭圆积分,很难将3个方程合并为1个方程从而直接由d求得p.Sridharan等[18]建议通过拟合方程中的u和Kd得到拟合关系式,再将拟合式代入式(3)得到p关于d的函数.详细过程如下:假设一系列p,可以由式(3)得到一系列u,已知σ和u可以由式(1)得到z,再通过精确的数值积分可以得到与u对应的Kd,最后将u和Kd拟合即可得拟合关系式,其形式一般为
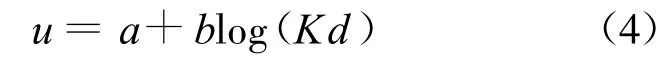
其中常数a和b仅受σ和n的影响.用这种方法得到的拟合式相关系数一般可达0.99.再将式(4)代入式(3)即可得Gouy-Chapman模型的拟合形式:
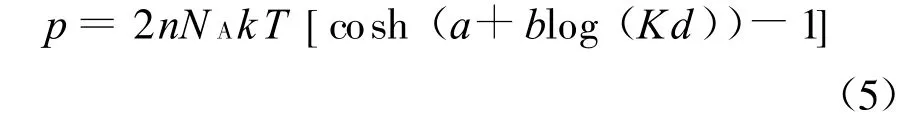
Zhang等的试验中所加的膨胀压力π实际等于双电层斥力和范德华力之差,范德华力的表达式为[15]
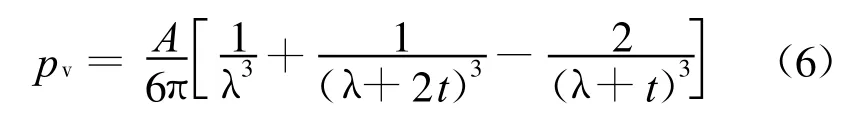
式中:A=2.2×10-20J,为 Hamaker常数;t为晶层的厚度,一般取0.93 nm.从而有

用上式对Zhang等的试验数据进行拟合,结果如图1所示.从图1可以看出,当晶层外的平衡电解质浓度n≤0.01 mol/L时,式(7)能较好地拟合试验数据,但是在n为0.1和0.3 mol/L两种情况下,当膨胀压力大于200 kPa时,理论值和试验值产生偏差.原因可能在于当平衡电解质浓度较大时,晶层间离子浓度也随之增大,随着晶层间距的减小,离子水合产生的水合力影响逐渐显现,使得仅仅用双电层理论计算的理论结果小于试验结果.
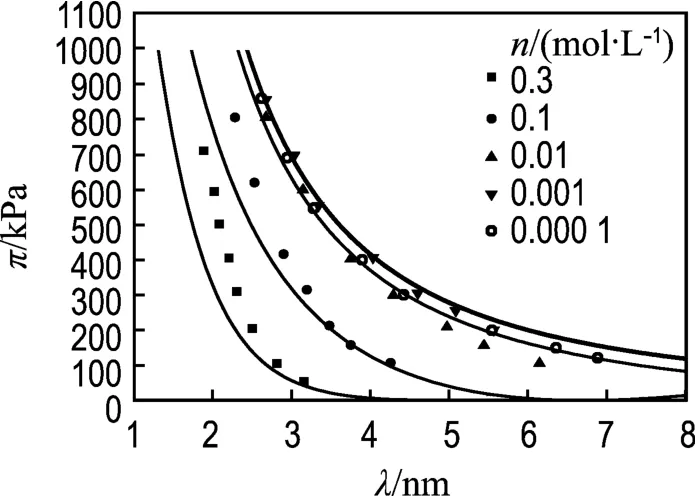
图 1 π-λ的试验点及 Gouy-Chapman模型拟合曲线Fig.1 Experimental points for π-λ together with the predicted curves calculated by the Gouy-Chapman model
用同样的计算方法,对文献[14]的试验数据拟合结果如图2所示.试验用Hectorite土的表面电荷密度σ大约为 0.001 C/m2,电解质浓度为10-5mol/L.需要注意的是,文献[14]中晶层间的作用是从能量的角度表示的,本文中转化为压强形式.
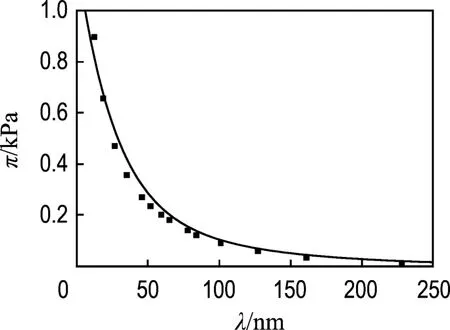
图2 对文献[14]试验数据的拟合结果Fig.2 Fitting results on the experimental data of Lit.[14]
Quirk等[15]从另外一个角度用Gouy-Chapman模型对Zhang的数据进行拟合,式(2)用一个椭圆函数来表示.计算过程如下:已知膨胀压力和与之对应的晶层间距的试验值πexp和λexp,可以由λexp通过式(6)得 pv,进而由式(7)求得双电层斥力p,然后由式(3)得 u,已知σ,则z可通过式(1)求得,u和z都已知后通过数值方法解椭圆函数即可得Kd,最后可求得晶层间距理论值λth.计算结果如图3所示.
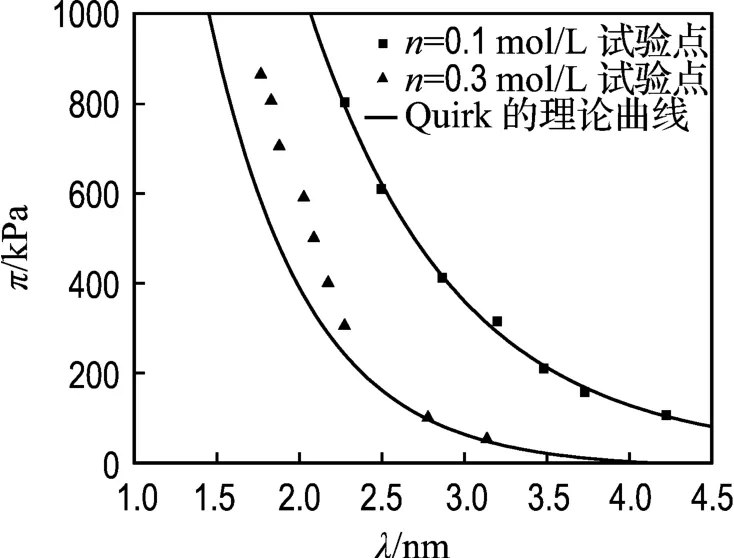
图3 π-λ的试验点以及Quirk的理论曲线Fig.3 Experimental points for π-λtogether with the theoretical curves presented by Quirk
从图 3可知,当 n=0.1 mol/L时,采用Quirk的方法计算结果和试验数据能够吻合,但是当n=0.3 mol/L时,拟合效果同样不理想.因为Quirk采用的方法是逆推法,前提是λ和π的试验值都已知,才能推得 λth,当用 λexp求得 pv,并由式(7)求得p的同时,也将可能存在的水合力转移到双电层斥力p上,才使得λth能与试验值基本吻合.然而当n=0.3 mol/L时拟合的结果不准确说明这种逆推法当存在水合力时可能存在偶然性.而且,这种方法只能用来验证双电层的适用性,并不能由晶层间距预测膨胀压力.
用式(7)对Viani等[17]的一组试验数据拟合结果如图4所示,Viani的这组试验用土与Zhang的试验用土都是Upton蒙脱石,而且用的试验仪器一样,但试验结果却有偏差.Zhang对此的解释是:虽然两人都是用X光衍射法测得晶层间距λ,然而处理数据的方法不同导致了试验结果的偏离.Zhang建议将Viani的试验点向右平移0.25 nm两种试验结果就会一致,即如果采用Zhang的方法处理数据,Viani的试验结果也基本符合双电层理论.
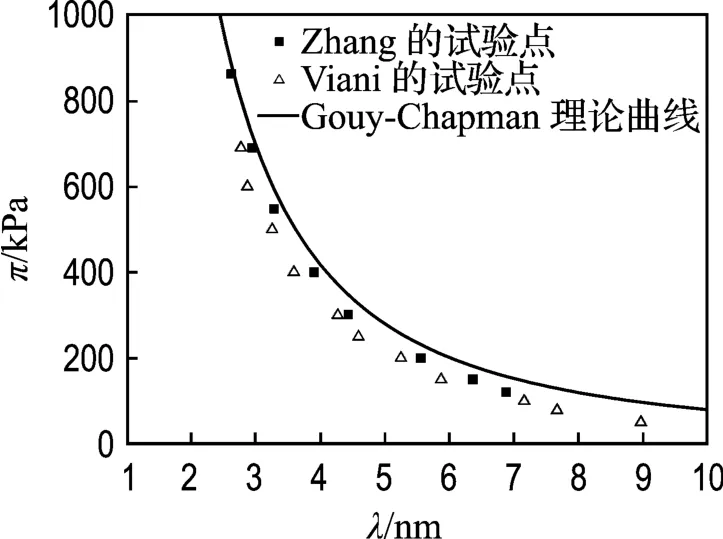
图4 n=0.0001 mol/L时,Zhang和 Viani的 π-λ试验点以及Gouy-Chapman模型理论曲线Fig.4 Relation between πand λat 0.0001 mol/L obtained by Zhang and Vianiand the theoretical curve of Gouy-Chapman model
1.2 对晶层间距-电解质浓度关系的验证
Zhang等不赞成双电层理论的另一个理由是当膨胀压力π为定值时,晶层间距λ随平衡电解质浓度n变化的试验结果与用Gouy-Chapman模型计算得到的理论值不一致.本文接下来的验证将说明平衡电解质浓度对晶层间距的影响基本符合双电层理论.
n 分别取 0.1、0.01 、0.001、0.0001 mol/L,将膨胀压力试验值πexp代入式(7),从而求得理论晶层间距λth,将πexp对应的晶层间距理论值和试验值对比如图5所示.n没有取0.3 mol/L是考虑到此时的水合力影响较大.π之所以取200、300、400 kPa,是因为此3种情况下都有试验数据.
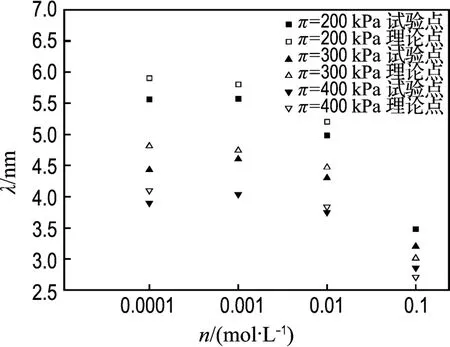
图5 不同 π值晶层间距λ随电解质浓度n变化的试验点与理论结果的比较Fig.5 Comparisons of the observed points of λvs.n with the theoretical values at different designated values of π
从图5可以看到,Gouy-Chapman模型的理论值和试验值基本一致或接近.说明当膨胀压力不变,0.0001 mol/L≤n≤0.1 mol/L时,晶层间距随电解质浓度的变化基本符合Gouy-Chapman双电层模型.
1.3 简化的Gouy-Chapman模型
奥尔芬[1]曾指出,当间距为 2d的平行晶层间的双电层相互作用较弱时(Kd>1),可以将平行晶层中平面处的电势等价于两个独立的双电层在离表面距离为d处的电势之和,即[1]
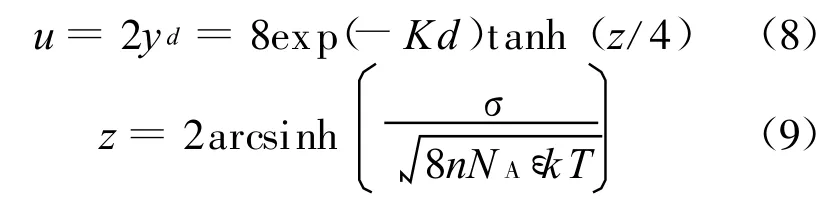
式中z为独立晶层表面量纲一电势.由于双电层相互作用较弱时u较小,式(3)可借助泰勒级数简化为
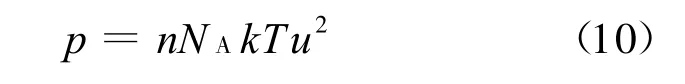
将式(8)、(9)代入式(10)即可得简化的Gouy-Chapman模型:
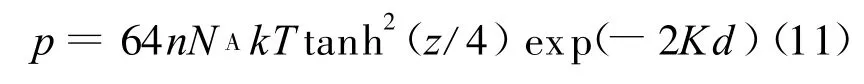
对于Gouy-Chapman双电层模型,σ=0.108 C/m2,n=0.01、0.001 mol/L时,K 分别为0.325、0.1027 nm-1,根据1.1介绍的方法可得u-Kd拟合式分别为

其相关系数R2=0.9999,所以可以用上式代替u、Kd的数值解代入式(3)与式(11)进行比较,结果如图6所示.
从图中可以看出,Kd<1时两种曲线有偏差,尤其当Kd<0.75以后;而Kd>1时,两种曲线几乎重合,此时可以用简化的模型代替Gouy-Chapman模型.虽然简化 Gouy-Chapman模型不用求解椭圆积分,较Gouy-Chapman模型简单,但是这里仅仅给出了两种情况,并不能说明所有情况下Kd>1时简化模型都能适用,而Gouy-Chapman模型的拟合形式并不受Kd的影响,因此采用Gouy-Chapman模型还是简化模型的拟合形式需要根据具体问题来选择.
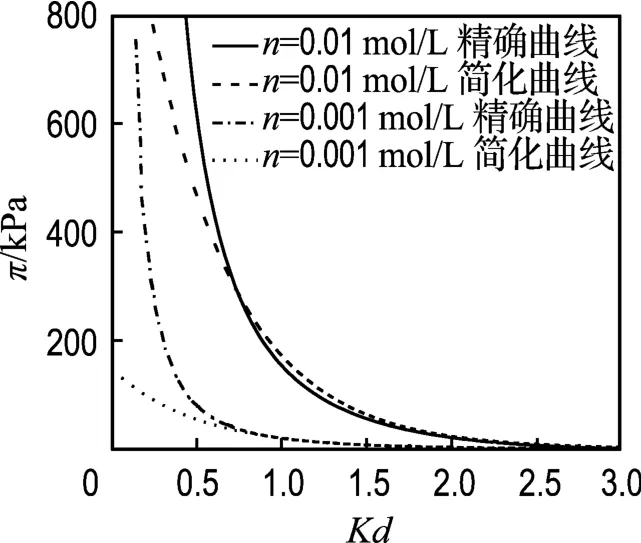
图6 Gouy-Chapman模型曲线与简化Gouy-Chapman模型曲线的比较Fig.6 Comparisons of the Gouy-Chapman model curves with the simplified Gouy-Chapman model curves
2 讨 论
(1)Zhang等[3]所做的试验仅仅是为了研究晶层间或相互平行的颗粒间的作用力,所以本文讨论的Gouy-Chapman模型仅限于模拟平行晶层或平行颗粒间的长程相互作用,并不能直接应用于具有宏观尺寸的土体试样,即不能将平行晶层或平行颗粒间的膨胀压力等同于膨胀土宏观试样的膨胀压力,因为宏观试样中颗粒的取向随机分布,这样一方面会导致颗粒间呈边-面结合,因此产生的静电力以及颗粒间的相互作用会影响单个颗粒内部或颗粒间产生的膨胀压力在宏观试样上的显现,另一方面,平行晶层或平行颗粒间产生的膨胀压力不会只在试样的一个方向显现,竖向的膨胀压力并不等于总膨胀压力.如何将细观的膨胀压力平均至宏观尺度将是下一步的努力方向.
(2)直接量测晶层间作用力和晶层间距的方法主要有Zhang等[3]所用的传统方法,这种方法是通过氮气对试样加压的同时用X光衍射仪对晶层间距进行观测.较为精确的仪器有Israelachvili[11]研制的表面测力仪(SFA)以及原子力显微镜(AFM).Liang等[20]对两种仪器进行了对比.本文中Nishmura等[14]的试验数据即为AFM所测结果.
(3)图1中,n≤0.01 mol/L的情况下,当膨胀压力小于200 kPa时,Gouy-Chapman模型的预测结果与试验数据稍有偏差,这可能是由电荷规则(charge regulation)效应引起的.Chan等[21]用考虑电荷规则效应的Gouy-Chapman-Stern-Grahame模型对双电层相互作用力进行了解释,在低压力时拟合效果较好,但是在高压力下,结果并不理想.
3 结 论
(1)当n≤0.01 mol/L时,Gouy-Chapman模型能够较好地模拟膨胀压力π和晶层间距λ之间的关系;当n为0.1和0.3 mol/L时,由于受晶层间水合力的影响,π-λ关系部分服从 Gouy-Chapman模型.
(2)当膨胀压力为定值,0.0001 mol/L≤n≤0.1 mol/L时,晶层间距随电解质浓度的变化与Gouy-Chapman模型的预测结果基本一致.
以上两方面的验证,说明在没有水合力的影响下蒙脱石晶层间的长程膨胀符合双电层理论,从而可以用Gouy-Chapman模型定量地模拟.
[1]范·奥尔芬.粘土胶体化学导论[M].许冀泉,等译.北京:农业出版社,1982
[2]NORRISH K.The swelling of montmorillonite[J].Discussions of the Faraday Society,1954,18(1):120-134
[3]ZHANG F S,LOW P F,ROTH C B.Effects of monovalent,exchangeable cations and electrolytes on the relation between swelling pressure and interlayer distance in montmorillonite[J].Journal of Colloid and Interface Science,1995,173(1):34-41
[4]ISRAELACHVILI J N,MCGUIGGAN P M.Forces between surfaces in liquids[J].Science, 1988,241(4867):795-780
[5]ISRAELACHVILI J N,WENNERSTROM H.Role of hydration and water structure in biological and colloidal interactions[J].Nature,1996,379(6562):219-225
[6]M ITCHELLJ K.Fundamentals ofSoil Behavior[M].New York:John Wiley&Sons,1976
[7]BRADY N C,WEIL R R.The Nature and Properties of Soils[M].New Jersey:Prentice Hall,1996
[8]VERWEY E J W,OVERBEEK J.Theory of the Stability of Lyophobic Colloids[M].Amsterdam:Elsevier,1948
[9]HIEMENZ P Z.胶体化学原理[M].周祖康,等译.北京:北京大学出版社,1986
[10]HUNTER R J.Foundations of Colloid Science:Vol.1[M].Oxford:Clarendon Press,1986
[11]ISRAELACHVILI J N.Intermolecular and Surface Forces[M].London:Academic Press,1985
[12]PASHLEY R M.DLVO and hydrationforces between mica surfaces in Li+,Na+,K+,and Cs+electrolyte solutions:A correlation of double-layer and hydration forces with surface cation exchange properties[J].Journal ofColloid and Interface Science,1981,83(2):531-546
[13]DUCKER W A,SENDEN T J,PARSHLEY R M.Direct measurement of colloidal forces using an atomic force microscope [J].Nature, 1991,353(6341):239-241
[14]NISHMURA S,KODAMA M,YAO K,et al.Directsurface force measurementforsynthetic smectites using the atomic force microscope[J].Langmuir,2002,18(12):4681-4688
[15]QUIRK JP,M ARCELJA S.Application of double-layer theories totheextensive crystalline swelling of Li-montmorillonite[J].Langmuir,1997,13(23):6241-6248
[16]LOW P F.Structural component of the swelling pressure of clays[J].Langmuir,1987,3(1):18-25
[17]VIANIB E,LOW P F,ROTH C B.Direct measurement of the relation between interlayer force and interlayer distance in the swelling of montmorillonite[J].Journal of Colloid and Interface Science,1983,96(1):229-244
[18]SRIDHARAN A,CHOUDHURY D.Swelling pressure of sodium montmorillonites [J].Geotechnique,2002,52(6):459-462
[19]LOW P F. The swelling of clay:Ⅱ.Montmorillonites[J].Soil Science Society of America Journal,1980,44(4):667-676
[20]LIANG Y C,HILAL N,LANGSYON P,et al.Interaction forcesbetween colloidalparticlesin liquid:Theoryand experiment[J].Advances in Colloid and Interface Science,2007, 134-135:151-166
[21]CHAN D Y C,HEALY T W,SUPASITI T,et al.Electrical double layer interations between dissimilar oxide surfaces with charge regulation and Stern-Grahame layers[J].Journal of Colloid and Interface Science,2006,296(1):150-158
