微孔电火花加工极间工作液流动状态研究
2010-09-28贾振元,郑新毅,王福吉,刘巍
贾 振 元, 郑 新 毅, 王 福 吉, 刘 巍
(大连理工大学精密与特种加工教育部重点实验室,辽宁大连 116024)
0 引 言
电火花加工广泛用于微小孔的加工,当使用电火花机床加工微孔时电极截面积小,容易变形、不易散热、排屑困难,因此电极损耗大、加工效率低.目前,进行微孔加工解决上述问题的方案是采用旋转头附件使工具电极转动或使工件转动,不仅可以提高加工速度,还可以提高加工孔的圆度[1].国内对于电极旋转问题的研究主要通过实验方法得到电极转速与加工时间的曲线,从而得到最佳转速[2].当前的电火花加工绝大多数为湿式加工,即工作区充满流动的工作液.由于工作液直接参与放电过程,其运动状态对放电过程的消电离时间和放电瞬间工作液成分会产生影响.放电加工的产物为电蚀微粒,微粒的动力稳定性和聚结不稳定性直接影响电火花加工过程的稳定性[3],而微粒的运动状态和工作液的流动有直接关系.电火花微孔加工放电间隙内的流场是典型的微流场,目前广泛应用的微流场检测手段为微观粒子图像测速技术(Micro-PIV),该方法只适合于透明基体材质的微流系统流场检测[4].而其他流场检测方法如X射线断层摄影法、X射线干涉测量法、荧光显微镜和强化CCD照相机图像记录法等,由于微孔电火花加工的放电间隙极小(一般为几μ m到几十μ m)[5],上述方法无法深入间隙内进行测量.
工作液的流动状态与加工过程的放电状态存在密切关系,无论放电状态检测还是机理研究都有必要对工作液的运动规律进行揭示.微细电火花加工过程中的工作液普遍使用去离子水,它属于典型的牛顿流体,可以采用流体力学理论用有限元的方法对工作液流场进行计算与研究.国外运用流体力学理论进行电火花研究重点是对放电机理的研究[6],本文拟从流场角度对微孔电火花加工过程进行详细论述,并将研究结果应用在直径小于0.1 mm的微孔电火花加工中,为其提供理论基础.
1 工作液流体运动学模型的建立
电火花加工中工作液的作用是:①形成火花击穿放电通道,在放电结束后迅速恢复间隙的绝缘状态,并对放电通道产生压缩作用,使放电能量集中;②流体的动力作用使电蚀产物抛出和排除;③对工具、工件起冷却作用,防止氧化、避免烧伤.目前的工作液主要为煤油、各种乳化油和纯水,在电火花微细加工中普遍使用纯水作为工作液,它是典型的牛顿流体.电极的旋转会带动工作液运动,所以电极与工作液间存在摩擦力,在计算时要考虑流体的粘性.虽然电火花加工过程中有热量放出,但产生热量很小,工作液又是循环流动的,通过热传递很快达到平衡,可以不考虑能量的影响.加工过程中工作液恒定、流动是非定常的.在重力场中只考虑z方向的质量力.描述流体的控制方程包括连续方程、动量方程、湍流模型方程,湍流模型选用工程上应用较广的κ-ε双方程模型.适合电火花加工旋转电极周围流体的各个控制方程如下[7].
工作液流体的张量连续性方程:

式中:ui为速度u在第i个方向的分量,i∈{1,2,3};xi为第i个方向坐标.
工作液流体的张量运动微分方程:

式中:i,j∈{1,2,3};fj为流体在第j个方向上的质量力,其中 f1=f2=0,f3=-gz;ν为流体运动粘度系数;ρ为流体密度;g为重力加速度;p为流体内部压强.
湍动能k张量方程:
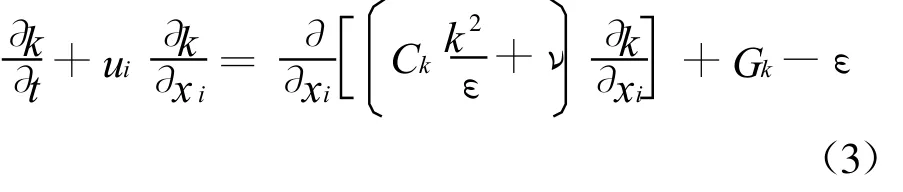
湍动能耗散率ε张量方程:

方程(3)、(4)中:Gk是由于平均速度梯度引起的湍动能k的产生项,

式中:Cμ为常值,取0.09.Ck一般取0.09~0.11;Cε一般取0.07 ~ 0.09;Cε 1一般取1.41~ 1.45;Cε 2一般取1.91 ~ 1.92.
上述描述工作液流体运动的方程属于非线性守恒偏微分方程组,需通过数值方法进行有限元分析.
2 放电间隙内流场计算与模拟
2.1 流场分析模型的建立
以0.1 mm电极加工深度为1 mm孔为例进行建模,放电间隙为 10 μ m.工作液为纯水,是典型的牛顿流体,温度为25℃时其动力粘度 μ=8.94×10-4Pa·s、运动粘度ν=8.97×10-7m2/s.
在实际加工过程中工作液充满放电间隙且液面高出工件一定距离,工作液上方为大气.气相和液相的分布模型如图1所示,这样建立模型可以表现液面的波动情况.在GAMEBIT软件中建立流体模拟模型如图2所示,并进行网格划分:网格类型为四面体结构,划分策略为主要采用四面体单元,适当的地方用六面体、锥体或楔体等单元.最后指定边界条件:运动边界为旋转电极,速度为10000 r/min.

图1 微孔电火花加工流场结构模型Fig.1 Structure model of flow field in micro-EDM

图2 工作液流体求解模型Fig.2 Solution model of working fluid
模型建好后导入FLUENT软件中进行求解.解算器选择分离解算器;非定常流动;流体模型为VOF模型:基本相为空气,第二相为水;流动模型为标准k-ε双方程模型;计算环境考虑重力影响,定义大气压力作用在入口处;方程离散格式选一阶迎风格式.
2.2 结果流态分析
(1)电极端面的速度流线
速度分布曲线可展示流体的流动状态和规律,图3为距孔底 3 μ m处的速度流线分布,图 4为距孔底6 μ m处的速度流线分布,从图3和图4的速度流线可知:电极端面的流动为层流;底层平均速度很小,中心处速度很低,切屑很容易在此处沉积.

图3 距孔底 3 μ m处速度流线Fig.3 Velocity contours in 3 μ m high

图4 距孔底 6 μ m处速度流线Fig.4 Velocity contours in 6 μ m high
(2)电极周围的速度流线和半径方向速度分布
通过电极截面速度流线可以看出电极周围放电间隙内工作液的流动为层流,如图5所示.速度分布曲线表明:在放电间隙内电极表面的速度最高为电极转速,孔壁的速度为零,速度以一定梯度由电极表面向孔壁递减,如图6所示.具体分布方程如下:
速度vθ分布方程

电极转速ω=10000 r/min,代入方程(6)得


图5 电极周围速度流线Fig.5 Velocity contours around electrode

图6 电极周围速度分布曲线Fig.6 Velocity distribution curve around electrode
(3)压力分布和液面形状
图7为孔底到液面的静态压力分布曲线,纵坐标是与标准大气压力的差值,z=1.0~1.2 mm为气相,大气压作用在此处相对压力为0.随着z值减小压力逐渐增加,越向孔底压力越大.但是因距离短压力增加的幅度也小:从孔底到液面工作液的深度为1 mm,压力仅增加了1.2 Pa.而且由于间隙很小,内部的工作液像薄膜一样分布,在电极带动下运动时厚度分布不均,所以压力呈波动性递增.
图8是气液两相交界面的液面分布,从图中可见靠近电极的中心处液面稍高,液面呈一定波形.电极周围的工作液在电极带动下会以一定速度旋转,由于离心力的作用向远离电极的方向运动,导致周围液面高、中心液面低,液面呈现波动;又流场中的流动速度很低,粘性力起主要作用,靠近电极的流体会附着在电极上随着液面波动,所以电极表面的液面高,整个液面的分布规律为高低高趋势.
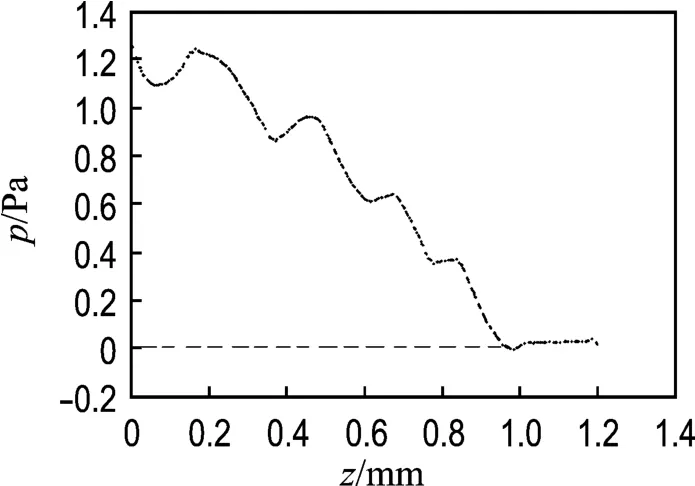
图7 压力分布曲线Fig.7 Pressure distribution curve
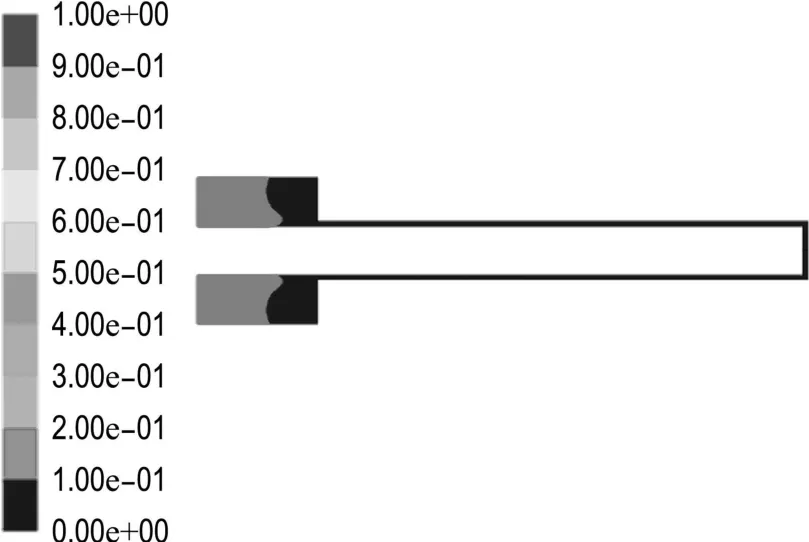
图8 气液两相交界面Fig.8 Interface between gas phase and liquid phase
(4)z方向速度分布
通过z方向的速度分布图(图9)可见,放电间隙内没有z方向上升或下降的速度分量,若要使电蚀产物排除到工作区以外只能靠放电爆炸力产生的冲击波促使轴向产生流体脉动,但微细电火花加工每次放电的能量很小,产生的放电爆炸力不足以将电蚀产物排除,所以定时抬刀仍然是必要的手段.

图9 轴(z)向速度分布曲线Fig.9 Velocity distribution curve of axis(z)direction
电火花微细加工中电源的单个脉冲能量小,一般在10-6~10-7J,从而使放电间隙更小,间隙值分布在几μ m到几十μ m范围内.以上得到了放电间隙内流场的计算结果,可见旋转电极周围的工作液恰好满足流体力学间隙流动的条件:①研究对象为不可压缩流体,密度恒定;②流体质点的运动惯性力和质量力均忽略不计;③流体的粘度不变;④近似为一维流动,流体质点沿壁面作平行流动,沿高度方向速度分量为零.由此,旋转电极电火花微细孔加工过程中工作液的流动问题可以简化为间隙流动模型进行分析,以减少流场计算的计算量、提高计算效率,而且不失准确性.
3 流场运动状态对电蚀产物分散相的影响规律
在电火花加工过程中,电蚀产物分散在极间工作液中构成一种分散系统.分散系统中微粒的动力稳定性和聚结不稳定性直接对加工过程产生影响.在电极旋转电火花加工中微粒的运动状态和工作液的流动直接相关:当电极旋转时,流动的工作液使电蚀产物以一定规律分布在放电间隙内,如果放电产物聚集,会使放电间隙减小造成短路;如果电蚀产物分散均匀,则放电容易进行,能提高电火花利用率.可见针对电极旋转电火花加工寻求电蚀产物对放电状态的影响规律,对提高加工效率和稳定加工过程有重要作用.
在电蚀产物分散系统中根据分散相粒子的大小把分散系统分成3类:①分子(或离子)分散系统,也称真溶液,分散相粒子半径小于10-9m;②胶体分散系统,分散相粒子半径为10-9~10-7m;③粗分散系统,主要为金属蚀除微粒,分散相粒子半径大于10-7m[3].其中胶体分散系统和粗分散系统都直接影响放电状态,但粗分散系统的微粒尺寸比较大,影响作用也更明显,本文重点对其进行研究.
图10为不同电极转速下工作液流体的速度分布曲线.电极旋转过程中放电间隙内的工作液在靠近孔壁的位置(r=0.00006 m)速度为零,在靠近电极表面的位置(r=0.00005 m)速度为电极旋转速度.由方程(7)可知无论电极转速如何变化,流场速度的变化规律都是相同的:靠近孔壁的速度始终为零,即图10中各条速度曲线与横轴的交点坐标不变;各条速度曲线与纵轴的交点坐标不同,为各个转速下的速度值.当电极转速提高时,速度分布曲线的斜率变大.此时流场中的粗粒子在靠近电极表面的位置将获得最高的速度做圆周运动,同时产生最大的离心力,当流体提供的向心力与离心力不平衡时,粒子会不断向远离电极的方向运动,直到附着在孔壁上.下面对粗微粒与流场速度的关系进行研究,由于颗粒的尺寸分布不均匀,只针对典型的球形粒子进行计算,且电极转速恒定.
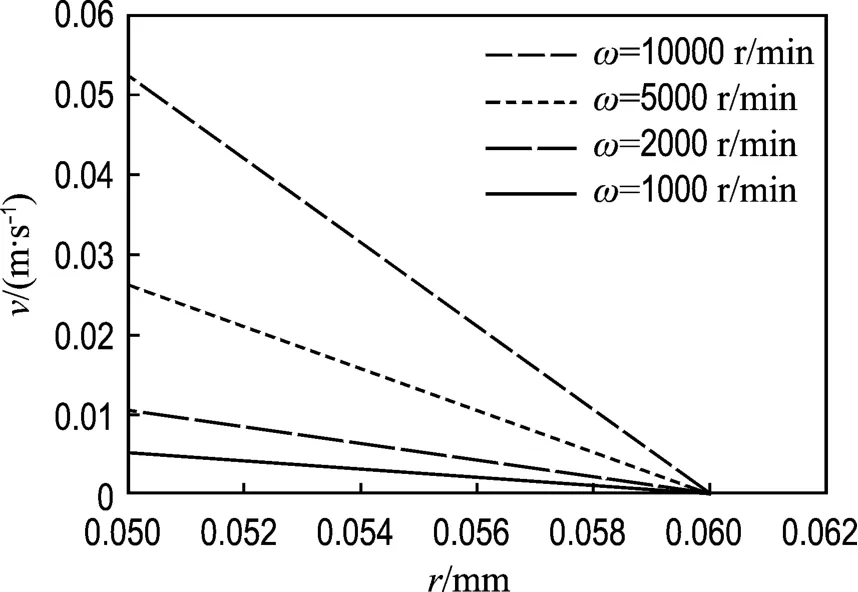
图10 不同电极转速下的速度分布Fig.10 Velocity distribution of different rotation speed
粒子做圆周运动时产生的离心力为[8]

式中:d为粒子直径;ρs为粒子固体密度;ρ为液体密度.
粒子运动的向心力由流体的摩擦力Fd提供:

当F
4 结 论
(1)根据建立的工作液流动状态有限元分析模型,得到放电间隙内工作液的流动规律:速度分布从电极周围到孔壁呈线性递减,电极周围工作液的流动状态为层流,流场中无竖直方向的速度分量.
(2)采用FLUENT软件计算与模拟微孔电火花加工流场,结果表明加工过程中工作液的运动服从间隙流动规律.
(3)通过对电蚀产物中粗微粒运动状态的分析,从放电产物角度得到了影响放电状态的因素,若要获得良好的放电状态应采用正极性加工并减小脉冲能量或保持脉冲能量不变减小脉宽.
[1]赵万生.先进电火花加工技术[M].北京:国防工业出版社,2003
[2]贾宝贤,赵万生,王振龙,等.微细电火花机床及其关键技术研究[J].哈尔滨工业大学学报,2006,38(8):402-405
[3]李明辉.电火花加工理论基础[M].北京:国防工业出版社,1989
[4]谢海波,傅 新,杨华勇,等.典型微管道流场数值模拟与Micro-PIV检测研究[J].机械工程学报,2006,42(5):32-38
[5]贾振元,顾 丰.基于信噪比与灰关联度的电火花微小孔加工工艺参数的优化[J].机械工程学报,2007,43(7):63-67
[6]EUBANK P T,PA TEL M R,BARRUFET M A,et al.Theoretical models of the electrical discharge machining process.III.The variable mass,cylindrical plasmamodel[J].Journal ofApplied Physics,1993,73(11):7900-7909
[7]张鸣远,景思睿,李国君.高等工程流体力学[M].西安:西安交通大学出版社,2006
[8]郭烈锦.两相与多相流动力学[M].西安:西安交通大学出版社,2002
