航空弧齿锥齿轮低噪声和低安装误差敏感性设计

刘光磊，樊红卫，谷霁红，江 平

（1.西北工业大学机电学院，西安 710072；2.中国航空动力机械研究所，湖南株洲 412002）

1 引言

弧齿锥齿轮因具有传动平稳、承载能力强等优点，被广泛应用于航空发动机和汽车的传动系统中。传动误差和齿面接触印痕是评价弧齿锥齿轮传动性能和加工质量的重要指标。传统的设计方法认为表征齿面接触印痕走向的啮合迹线应该与齿轮的根锥母线垂直[1]，但按这样的方法设计的弧齿锥齿轮副对安装误差比较敏感，且用传统设计方法得到的弧齿锥齿轮副传动误差曲线为分段的线性函数，在啮合周期的转换点处会产生较大的冲击、振动与噪声[2]。

Faydor L.Litvin教授提出了齿面局部综合法[2,3]，可以预控齿面的几何形状，能够得到稳定的接触印痕和对称抛物线型的传动误差曲线，同时可以得到比较理想的小轮加工参数。在国内，方宗德教授率先引进了局部综合法，并在此基础上开展了诸多新的研究[4]。但这些研究都没有将TCA（Tooth Contact Analysis，轮齿接触分析）仿真所得到的实际传动误差曲线与局部综合法所预置的理论传动误差曲线作对比，无法有效地证明该算法的正确性。

本文基于局部综合法，对某型航空弧齿锥齿轮副进行了齿面接触仿真分析，得到了倾斜的直线型齿面啮合迹线和对称的抛物线型传动误差曲线，并且，由TCA仿真得到的传动误差曲线与预置的传动误差曲线较好地吻合，有利于吸收齿轮副啮合时的振动与噪声，并可以降低齿轮副对安装误差的敏感性，对于研制工作在高速、重载工况下的航空发动机弧齿锥齿轮副具有十分重要的实际意义。

2 局部综合法原理

局部综合法是弧齿锥齿轮加工参数设计的最先进方法之一。通过控制传动误差曲线的2阶导数和齿面在参考点处啮合时的接触状态，来控制齿面的啮合性能，并据此确定大轮和小轮的加工参数。

文献[2，3]根据配对齿面∑(1)与∑(2)之间的曲率关系，给出了局部综合法的基本方程组[2,3]

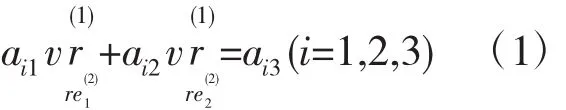
式中：系数ai1、ai2和ai3的详细表达式见文献 [2，3]；和为啮合点相对于齿面∑(1)的滑动速度沿齿面 2 个主方向的分量。

加工弧齿锥齿轮副时，刀具切削锥面与齿面处于线接触状态，故式（1）的解不惟一。此时，有如下方程组成立[2,3]

当加工好的2齿轮对滚时，2轮的齿面处于点接触啮合状态，故式（1）有惟一解。此时，有如下方程成立[2,3]

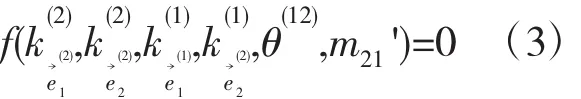
3 齿面方程与齿面接触分析

3.1 齿面方程

得到了齿轮副加工参数，便可由刀具齿面得到齿轮的齿面。通常，弧齿锥齿轮的小轮凹面主动，大轮凸面从动。以小轮凹面的形成过程为例，设Rc1为加工小轮凹面的外刀刀尖半径，αc1为外刀压力角，up和θp为外刀切削锥面坐标，为外刀切削锥面径矢，为外刀切削锥面法矢，则加工小轮凹面的外刀切削锥面如图1所示。图中阴影部分表示刀具的实体，反之表示空域。

在与小轮刀具相固连的坐标系Sc1中，加工小轮凹面的外刀切削锥面方程和法矢[3]为

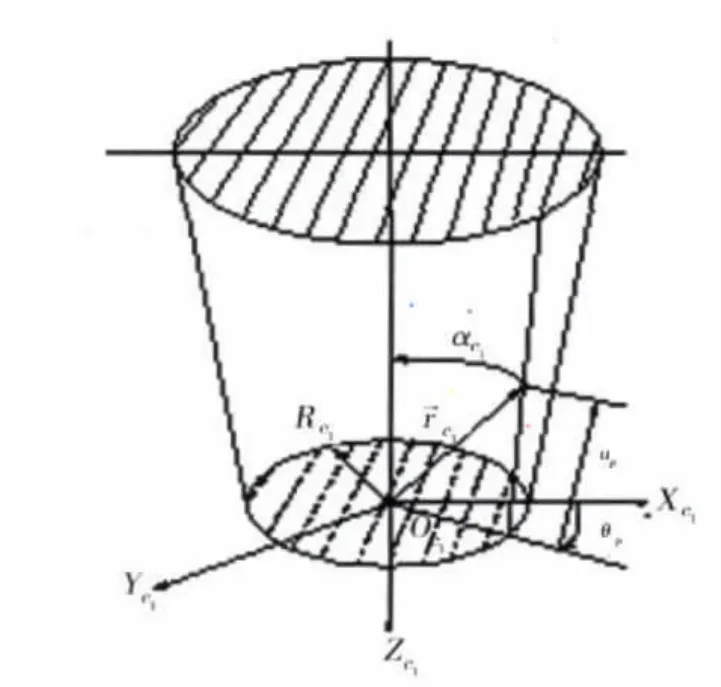
图1 加工小轮凹面的外刀切削锥面

小轮齿面是由刀具切削锥面依次经过摇台坐标系、机床坐标系、辅助坐标系和小轮自身坐标系4次转化后得到的。若用mi表示机床坐标系（i=1表示小轮，i=2表示大轮）、cri表示摇台坐标系，ci表示刀具坐标系、p表示小轮坐标系（g表示大轮坐标系），则小轮凹面方程和法矢[3]为

式中：f1为描述小轮安装位置的辅助坐标系；Mmn为从坐标系n向m转化的坐标变换矩阵。

对各坐标变换矩阵的详细表述，以及与小轮凹面配对啮合的大轮凸面的方程和法矢见文献[3]。

3.2 齿面接触分析

弧齿锥齿轮副啮合时，2齿轮的齿面从啮入到啮出始终连续相切接触，故在啮合固定坐标系Sh中，2齿面拥有公共的接触点，且在公共接触点处有公共法线，故有如下TCA基本方程组成立[3]

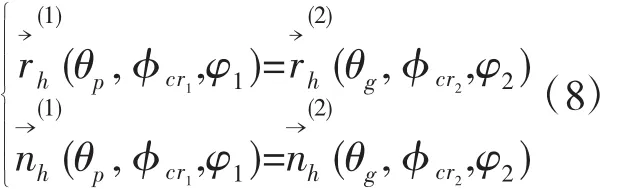
式中：θp、θg为加工小、大轮的刀刃位置；φcr1、φcr2为加工小、大轮的摇台转角，它们是描述小、大轮齿面的刀具参数；φ1、φ2为啮合时小、大轮的转角；矢量和表示齿面上任1点处的径矢和法矢。

求解式（8）可以得到弧齿锥齿轮副的齿面接触印痕和传动误差曲线。

4 传动误差与接触印痕

4.1 传动误差

进行TCA仿真时，传动误差函数 δ(φ1)[3,4]按下式计算

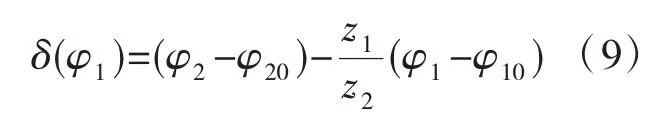
式中：φ10和φ20为2齿轮由参考点的加工状态到啮合状态需要转过的角度；z1和z2为2齿轮的齿数。

局部综合法预置的理论传动误差按下式计算

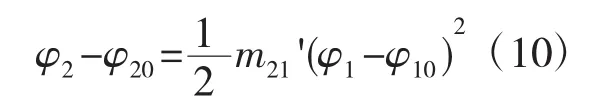
4.2 接触印痕

接触印痕包括齿面啮合迹线的倾斜方向和啮合点处的瞬时接触椭圆。基于局部综合法设计的啮合迹线可以在一定范围内倾斜，倾斜的啮合迹线能够提高齿轮副的重合度，保证啮合过程的平稳进行，且对安装误差不大敏感，在存在轻微安装误差的情况下仍能够正常工作。瞬时接触椭圆的大小则与轮齿的刚度和传动时所承受的载荷等因素有关。

4.2.1 齿面接触迹线

根据预置的大轮齿面接触迹线的切线方向与大轮刀具切削锥面第1主方向之间的夹角η2，由下式可求得小轮齿面啮合迹线的切线方向角

4.2.2 齿面接触椭圆

由弹性力学可知，点接触弧齿锥齿轮副在承载时会发生弹性变形，此时2齿面将由点接触延展为1小块面积接触。该接触面积在2齿面的公共切平面上的投影为1个近似的椭圆斑点。假设瞬时接触椭圆的长半轴长度为a、短半轴长度为b，则有[2,3]

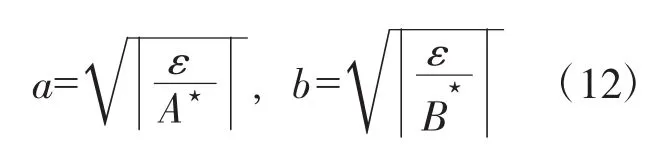
式中：ε为齿面间的压限量；A⋆和B⋆分别为长、短半轴影响因子，其计算公式见文献[3]。

5 算例

对38/43正交传动的航空弧齿锥齿轮副进行了齿面设计。以“小轮左旋、大轮右旋”的情况为例，轮坯几何参数见表1，大轮加工参数见表2，局部综合参数见表3，小轮加工参数见表4。图2、3分别为“小轮凹面推动大轮凸面”时的齿面接触印痕和传动误差曲线，图4、5分别为“大轮凹面推动小轮凸面”时的齿面接触印痕和传动误差曲线。各图中的3条实线表示相邻3对轮齿所生成的实际传动误差曲线，中间的1条虚线为预置的理论传动误差曲线。进行局部综合和TCA时，取格里森公司推荐的齿面压限量0.00635 mm。设计要求的传动误差幅值为7″。

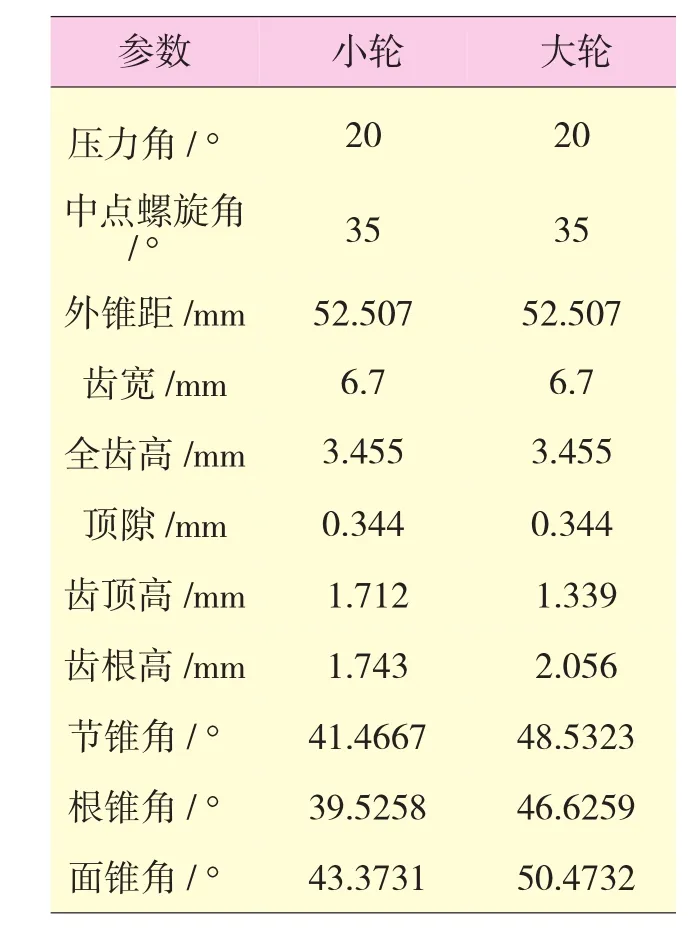
表1 轮坯几何参数

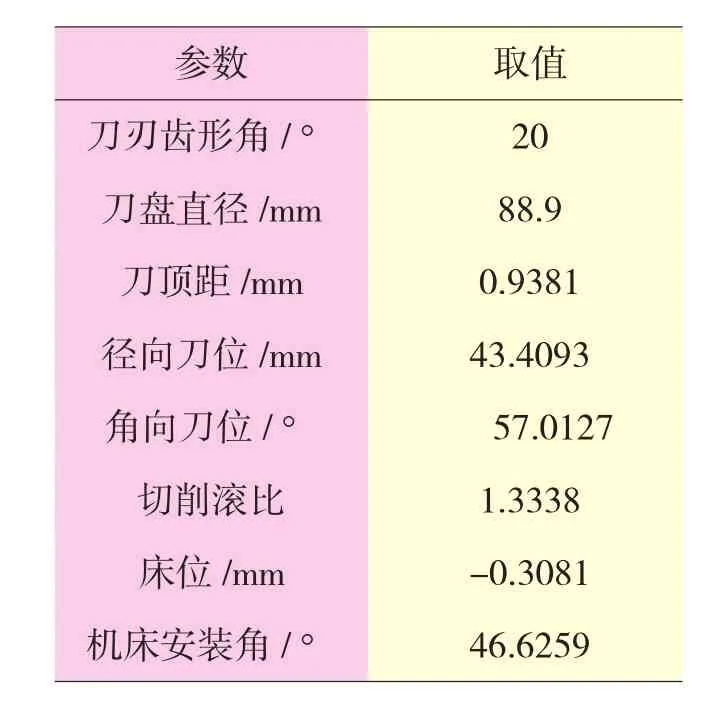
表2 大轮加工参数

表3 局部综合参数

表4 小轮加工参数

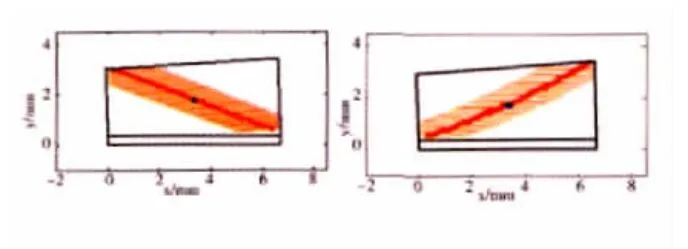
图2 “小轮凹面推动大轮凸面”时的齿面接触印痕

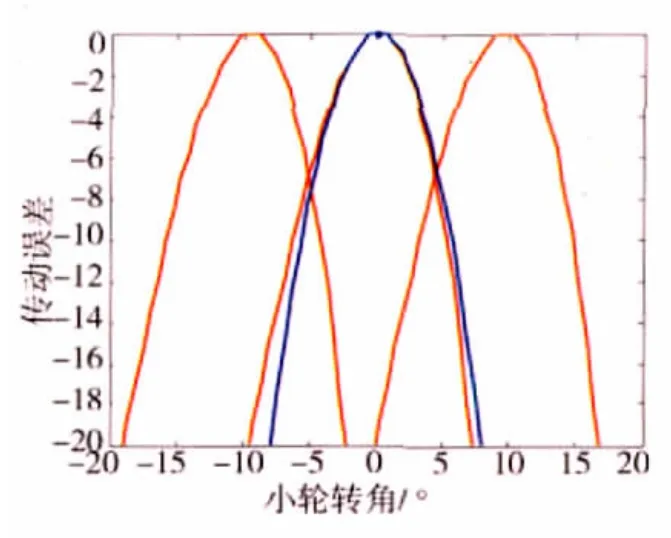
图3 “小轮凹面推动大轮凸面”时的传动误差曲线

图4 “大轮凹面推动小轮凸面”时的齿面接触印痕

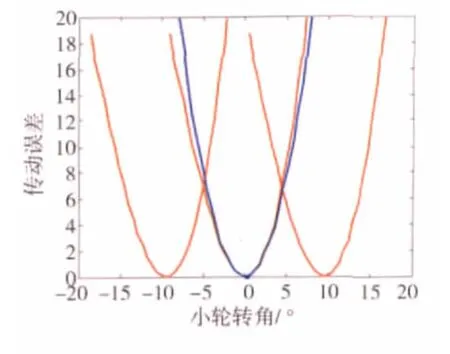
图5 “大轮凹面推动小轮凸面”时的传动误差曲线

从图2～5中可以看出，2种情况下的齿面啮合迹线基本都为直线，且接触印痕没有发生畸变。这是因为齿面接触印痕是由齿轮副加工参数完全且惟一特性决定的；传动误差曲线为对称性较好的抛物线，实际传动误差曲线与预置的理论传动误差曲线基本吻合，传动误差的幅值约为7.0157″，基本满足设计要求。

6 结论

（1）通过齿面局部综合与接触分析，将某型航空弧齿锥齿轮副的齿面啮合迹线设计成1条倾斜角度为21.478°（指大轮齿面参考点处的接触迹线切线方向与大轮刀具切削锥面第1主方向之间的夹角）的直线，将传动误差曲线设计成1条幅值为7.0157″的对称抛物线，有利于降低传动噪声和对安装误差的敏感性。

（2）TCA得到的传动误差曲线与预置的理论传动误差曲线基本吻合。

“小轮凹面推动大轮凸面”和“大轮凹面推动小轮凸面”2种情况的仿真结果都证明了上面2个结论，说明了本文所述方法的正确性。但是，在实际应用中，通常只采用“小轮凹面推动大轮凸面”的方法。

[1]L itvin F L,Fuentes A,Hayasaka K.Design,manufacture,stress analysis,and experimental tests of low-noise high endurance spiral bevel gears[J].Mechanism and Machine Theory,2006,41:83-118.

[2]Litvin F L著.齿轮几何学与应用理论[M].国楷，等译.上海：上海科学技术出版社，2008.

[3]Litvin FL,ZhangYi.Local Synthesis and Tooth Contact Analysis of Face-Milled Spiral Bevel Gears[R].NASA Office of Management Scientific and Technical Information Division,1991.

[4]方宗德,刘涛,邓效忠.基于传动误差设计的弧齿锥齿轮啮合分析[J].航空学报,2002,23(3):226-230.

[5]Litvin F L,Wang A G,Handschuh R F.Computerized generation and simulation of meshing and contact of spiral bevel gears with improved geometry[J].Computer methods in applied mechanics and engineering,1998,158:35-64.