航空发动机涡轮盘裂纹扩展分析

秦银雷，魏大盛，王延荣

(北京航空航天大学能源与动力工程学院,北京 100191)

1 引言

作为航空发动机热端部件的涡轮盘工作条件十分严酷，对其进行结构设计必须遵守相关结构强度准则，其中之一为涡轮盘在出现初始裂纹后应有足够的裂纹扩展寿命,以满足可靠性和耐久性需求。因此，随着长寿命及经济性要求的提高，涡轮盘损伤容限分析日益得到重视。

国内外针对涡轮盘损伤容限的研究已经开展了许多。宋迎东等[1]对粉末冶金涡轮盘进行了应力分析，成为构件疲劳寿命评估的基础；魏大盛[2]和陈勇[3]采用有限元方法对涡轮盘的裂纹扩展寿命进行了分析，但由于裂纹体有限元模型建立比较复杂、工作量较大，分析中都假设裂纹在扩展过程中保持形状不变，显然这种假设不能很好地反映实际情况。

本文采用Lin和Smith[4]提到的2自由度方法描述裂纹扩展，在通用有限元程序MARC中实现了涡轮盘裂纹扩展的模拟，并评估了涡轮盘寿命。

2 空心等厚盘角裂纹应力强度因子计算验证

在工程中，通常以线弹性断裂力学为基础，由Paris公式求得裂纹扩展寿命；而采用J积分法求解应力强度因子最为常见。Rise于1968年提出的J积分，最初并未考虑体积力的影响，但随着工程应用越来越广泛，人们开始提出修正形式，以考虑体积力对J积分的影响。MSC.MARC程序中的J积分表达式[5]为

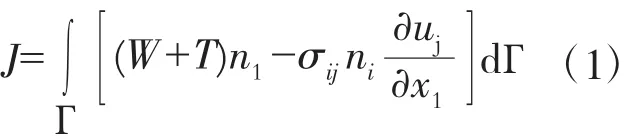
式中：W为应变能密度；T为动能密度，其引入使得J积分能够考虑体积力的影响。

在分析中，以MSC.MARC的断裂力学模块定义裂纹前沿，采用拓扑搜索方式确定J积分求解时的积分回路。裂纹前沿由一系列节点构成，得到每个节点的J积分值后，通过平面应变关系式可以求出对应于每个节点的应力强度因子，即

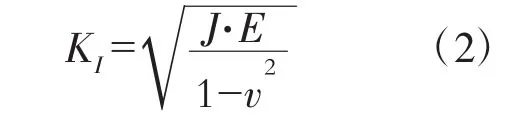
离心力是高速旋转的涡轮盘承受的主要载荷，因此，需要验证在离心力作用下，利用J积分法求解应力强度因子的计算精度。选取如图1所示的空心等厚盘作为算例。其几何尺寸为：r1=10 mm，r2=80 mm，t=20 mm，a=b=10 mm；材料为GH901合金，材料参数[6]：E=198000 MPa，μ=0.303，ρ=8.21×103kg/m3；疲劳裂纹扩展参数[7]为：C=6.2493e-12，m=4.6462；等厚盘转速为30000 r/min，轮缘无外载荷。

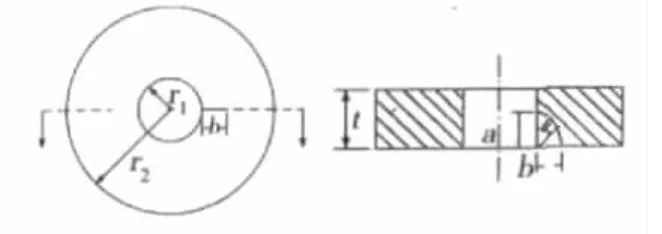
图1 等厚盘几何模型

含裂纹等厚盘的有限元模型如图2所示。首先，计算了不含裂纹时的应力状态，图3给出了等厚盘中心孔边周向应力的有限元计算结果，为440.9 MPa，与解析[8]429.64 MPa的相对误差为2.6%；其次，用J积分法计算了含裂纹时的应力强度因子值，图4给出了计算结果与手册解[9]之间的对照，最大相对误差为6%。从总体上看，应力强度因子沿裂纹前沿的变化趋势与手册解吻合得较好。由此可以得出：在体积力作用下，采用J积分法计算应力强度因子是可行的，且能达到一定的求解精度。

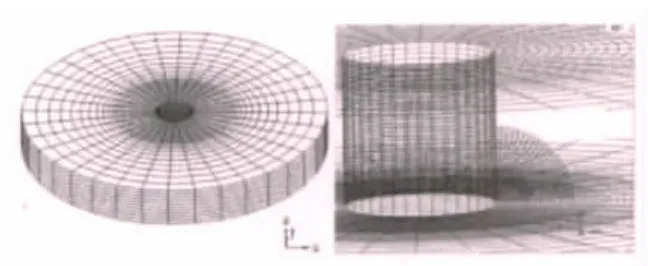
图2 等厚盘有限元模型及裂纹前沿网格

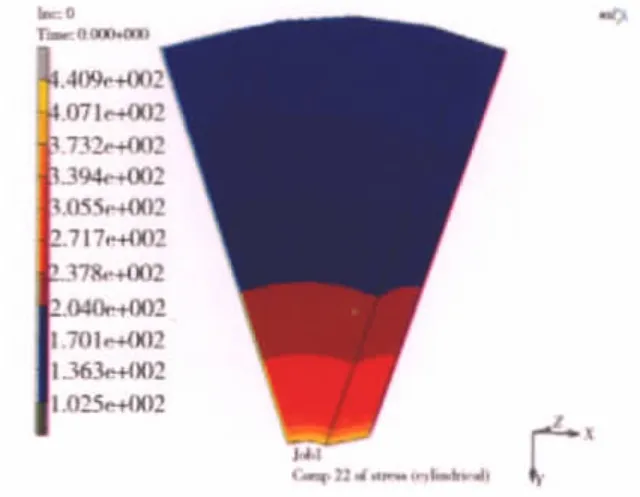
图3 等厚盘周向应力分布

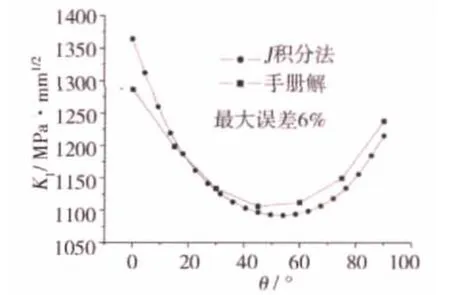
图4 等厚盘中心孔边角裂纹应力强度因子

3 涡轮盘裂纹扩展分析

3.1 涡轮盘应力分析

在进行涡轮盘裂纹扩展分析之前，应先明确裂纹容易萌生的位置，因此需要进行无裂纹时的涡轮盘应力分析。基于带孔涡轮盘的循环对称几何特性，选取1/16扇区，建立如图5所示的有限元模型。在转速为12640 r/min、轮缘均布外载荷为156.8 MPa的条件下，计算得到的周向应力和等效应力分布如图6所示。从图6中可见，周向应力最大值发生在螺栓孔的6点钟处，此处最容易萌生裂纹，且裂纹扩展的主要驱动力为周向应力。

图5 轮盘有限元网格

图6 涡轮盘应力分析

3.2 前沿几何形状在裂纹扩展中的变化

采用有限元方法模拟裂纹动态扩展的难点在于如何确定裂纹前沿每个节点的扩展方向和扩展过程中的裂纹前沿形状。

在建立含裂纹的涡轮盘有限元模型之前需要作以下假设：（1）初始裂纹形状为圆形角裂纹，位于螺栓孔周向应力最大处，且裂纹面法向同轮盘周向的应力方向一致；（2）裂纹扩展方向沿裂纹前沿的法向，且始终不偏离萌生时的轮盘子午面；（3）裂纹扩展规律符合Paris公式。初始裂纹深度（半径）取为0.25 mm，对裂纹局部的网格进行细化以保证计算精度，图7给出了裂纹前沿上的节点情况。

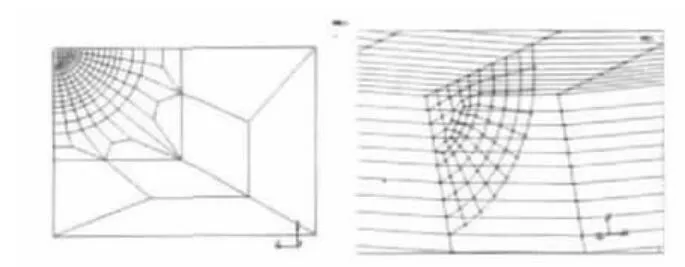
图7 裂纹前沿有限元网格及裂纹前沿节点

文献[4]提出了1种描述裂纹前沿形状发展变化的多自由度方法，即计算出裂纹前沿每个节点处的法向增量，来确定下一步裂纹前沿各节点的位置，然后通过3次样条曲线拟合这些节点，作为新的裂纹前沿。显然，采用这种方法进行扩展模拟，能更真实地反映裂纹扩展的情况；但由于涡轮盘的应力情况比较复杂，特别是螺栓孔边的应力集中，导致该处附近裂纹前沿节点（如图8所示中的A点）的应力强度因子较其它处的偏大，如果仍采用3次样条曲线来形成新的裂纹前沿，则建模比较困难。因此，采用2自由度法对裂纹的扩展路径进行了简化，即通过计算裂纹前沿两端（A、B）的增量，来确定下一步2点的位置（A′、B′），并以OA′、OB′分别作为等效椭圆的长、短轴。

由于等效椭圆包括3次样条曲线，这样的简化是偏于保守的。裂纹每扩展一步都需要重新划分裂纹附近的网格，通过指定裂纹扩展过程中的扩展增量来模拟轮盘裂纹扩展的过程，裂纹每步的扩展增量见表1。共进行了6步扩展，其中，0～3步的扩展增量沿孔轴向，4～5步的扩展增量沿孔径向；第4步时，裂纹穿透螺栓孔的轴向厚度变成穿透裂纹。

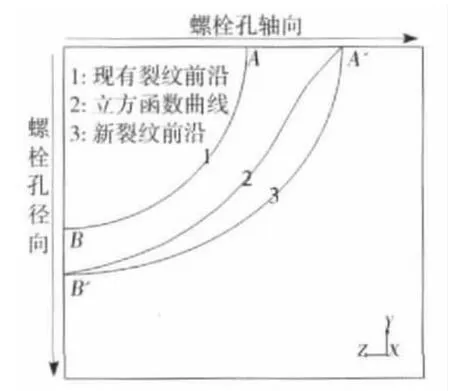
图8 裂纹前沿确定

表1 压力叶型受感部校准结果

在整个扩展过程中的裂纹形状变化情况如图9所示。前几步，裂纹形状变化不显著，这也是很多学者在处理复杂构件时假设裂纹形状保持不变的原因。需要说明的是，在裂纹穿透螺栓孔轴向厚度后，因有限元模型而导致的J积分的计算精度下降，但此时应力强度因子已经很大，裂纹扩展十分迅速，对剩余寿命影响不大。

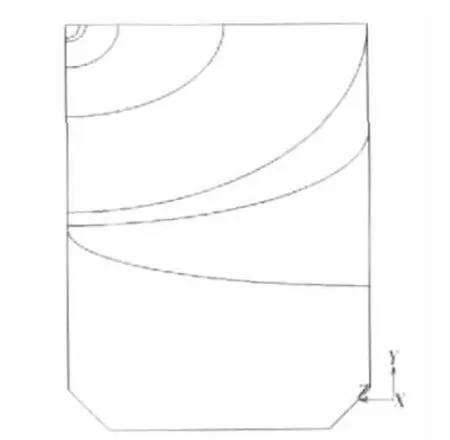
图9 裂纹形状变化

3.3 应力强度因子计算

利用J积分法计算应力强度因子。图10给出了裂纹穿透螺栓孔轴向厚度之前各增量步裂纹前沿应力强度因子的分布情况。从图10中可见，受螺栓孔边应力集中的影响，该处裂纹前沿节点的应力强度因子值都明显增大，裂纹沿螺栓孔轴向扩展速度较快，导致裂纹首先穿透厚度而成为穿透裂纹。

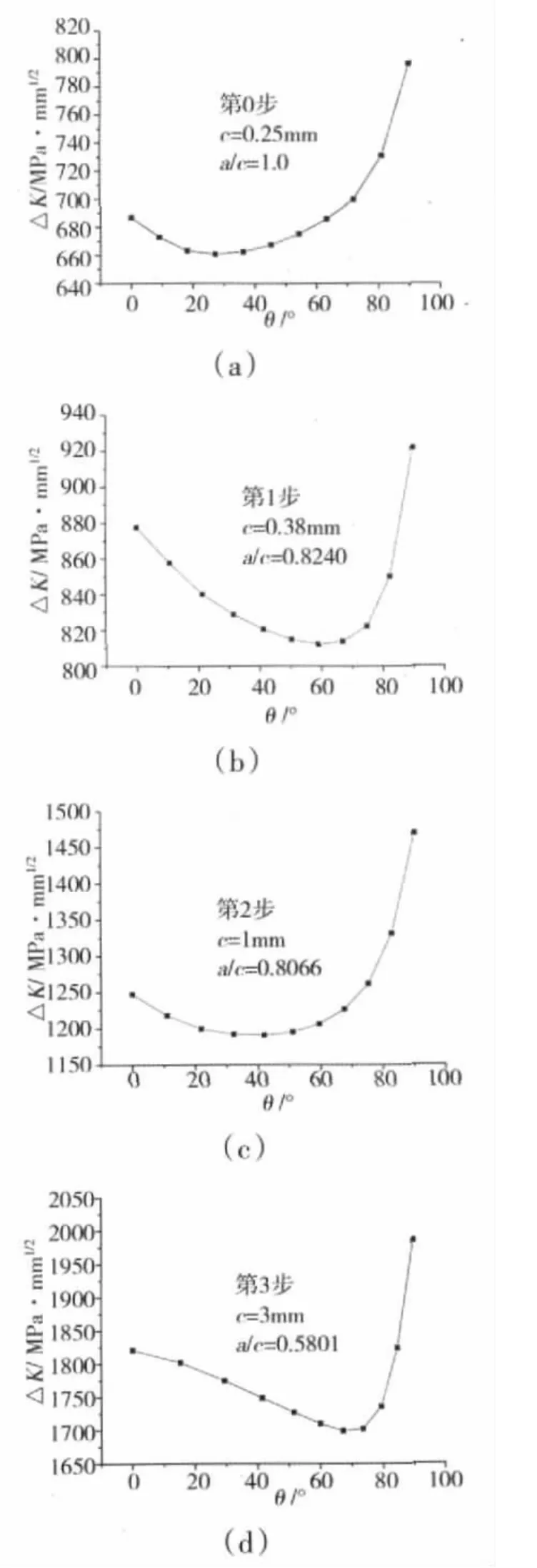
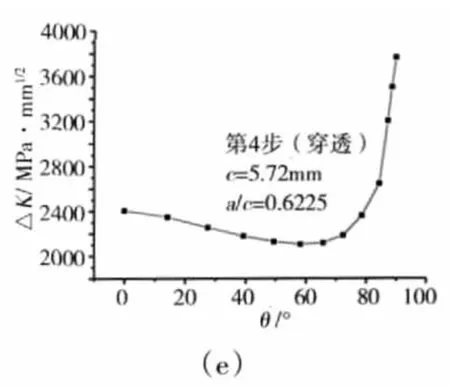
图10 裂纹前沿应力强度因子分布

3.4 涡轮盘裂纹扩展寿命分析

裂纹扩展寿命也就是含裂纹构件的剩余寿命。

裂纹在穿透螺栓孔的轴向厚度后，扩展速率非常快，因此，之后的循环寿命可忽略不计，而只需考查穿透之前的循环寿命。估算裂纹扩展寿命的方法为：将裂纹扩展区间按扩展增量步分为6个子扩展区间，即 0～1、1～2、2～3、3～4、4～5 和 5～6；假设在每个子扩展区间中应力强度因子范围(ΔK)保持不变，计算出每个子区间的扩展寿命后进行累加，即可得到总的剩余寿命，即

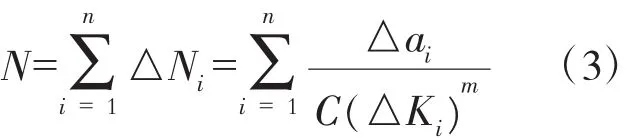
表2给出了每个子区间的扩展寿命和各初始尺寸所对应的剩余寿命。

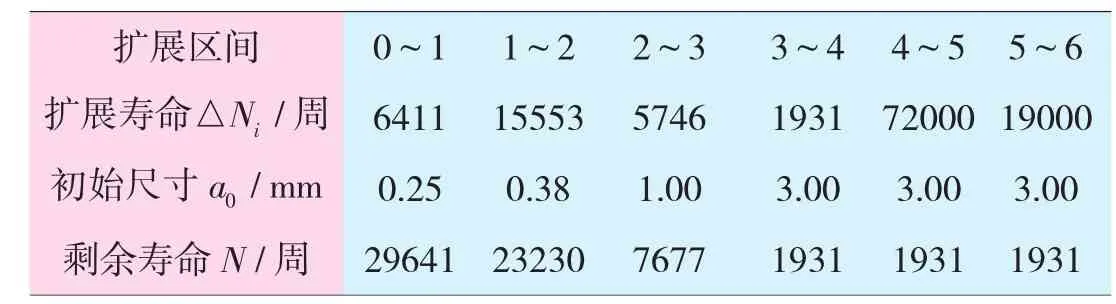
表2 涡轮盘裂纹扩展寿命有限元模拟结果

4 结论

以某航空发动机涡轮盘的裂纹为例，采用2自由度数值方法描述裂纹前沿在扩展过程中的形状变化，评估了涡轮盘剩余寿命，得到了一些具有工程参考意义的结论。

（1）对该涡轮盘而言，裂纹易萌生于螺栓孔处；一旦裂纹形成，就会先沿着螺栓孔的轴向方向扩展至轴向穿透，随后沿螺栓孔的径向扩展。

（2）由裂纹扩展寿命分析可知，寿命主要集中在裂纹扩展的前几步，如0.25～1 mm区间的扩展寿命约占整个扩展寿命的94%。

（3）所采用的模拟方法摆脱了形状保持不变的假设，更关注扩展过程的细节；虽然只是采用2点来确定裂纹前沿的形状，但较于形状不变的假设，能更真实地反映涡轮盘中裂纹扩展的情况。

值得注意的是，预测的构件剩余寿命与选取的裂纹扩展增量有很大关系。扩展增量越小，越能够反应实际情况，但工作量也会随之增加。因此，在实际工程应用中可以权衡二者之间的关系，而选取合适的裂纹扩展增量。

[1]宋迎东，陈伟，温卫东等.粉末冶金涡轮盘有限元应力分析[J].航空动力学报，1997，12(4)：422-424.

[2]魏大盛，王延荣.粉末冶金涡轮盘裂纹扩展寿命分析 [J]. 推进技术，2008，29(6)：753-758.

[3]陈勇.含夹杂粉末高温合金涡轮盘裂纹扩展寿命研究[D].南京：南京航空航天大学博士论文，2003.

[4]Lin X B,Smith R A.Finite element modeling of fatigue crack growth of surface cracked plates-PartI:The numerical technique[J].Engineering Fracture Mechanics, 1999, 63:503-522.

[5]MSC Marc Volume A.Theory and User Information[Z].Version 2005.MSC.Software Corporation，USA，2005.

[6]《中国航空材料手册》编辑委员会.中国航空材料手册[M].第2卷：变形高温合金铸造高温合金.北京：中国标准出版社，2001.

[7]陶表福，候静泳，谢济洲.GH901合金的高低周复合疲劳及其累积损伤研究[J].航空材料学报，1999，10(增刊)：35-43.

[8]宋兆泓.航空燃气涡轮发动机强度设计[M].北京：北京航空学院出版社，1987.

[9]中国航空研究院.应力强度因子手册[M].北京：科学出版社，1981.